基于中学物理课堂的数理融合教学环节设计

摘   要：数理融合是对数学和物理两门学科进行适度整合以培育学生通用素养为目标的教学活动。相较于单科教学模式，数理融合教学更注重知识的整合、聚焦思维培育，通过两门学科的认知交叉、聚合，促进基于学科又高于学科的多元化高阶能力形成，它的实施对培养学科核心素养有积极的推动作用。从数理融合角度对课堂教学环节重新设计，通过知识建构、知识整理、知识互联、知识回溯、知识内化等一系列教学实施实现融合知识的渗透、耦合与移植，让学生在多元的环境中把握物理的核心内涵，促进知识的内化和创新思维的形成。

关键词：教学；数理融合；知识互联；移植教学；知识回溯

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2025）1-0039-7

1    引   言

2022年4月教育部颁布《义务教育课程方案（2022年版）》，提出“设立跨学科主题学习活动，加强学科间相互关联，带动课程综合化实施，强化实践性要求。”［1］这意味着中学教学需要突破单学科的认识局限，要在学科交叉理念下审视中学教与学，通过适当的跨学科教学活动，以实现培养学生学科核心素养和通用素养的双重目标。作为一门建立在数学抽象基础上进行精准化描述的学科，物理与数学本身就存在千丝万缕的关系，物理是研究自然规律的主要描述工具，而数学是对物理规律的论证和量化表达，它是物理能够精准化描述自然现象的语言工具，反之物理的深入研究也会给数学的发展带来积极推动［2］。数理融合教学的意义在于深化学科间的连结，通过对数学、物理两门学科知识、思维的融合，创生出超越学科本身的思维认识，并对所学知识产生新的理解，形成不同于单学科的新解决策略，发展出新的统一性解释体系［3］。此外，这也是驱动学生学习方式从基础学习、研究性学习到学习学术转化［4］，以适应核心素养的高阶性期待，形成具有高品质的知识、思维和能力素养体系的重要途径。

2    教学环节设计

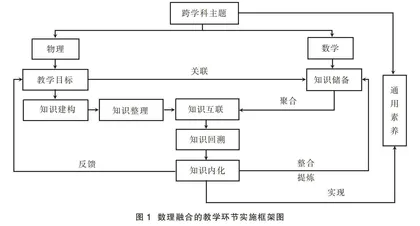
教学环节设计围绕跨学科主题展开，中学学科知识具有多样化和聚合性等特点，不同的学科内容应采用不同的教学方式以达到最优化的教学效果。因此，教师应筛选课程中有数理跨学科特征或需求的内容聚焦出跨学科主题，开展跨学科活动，从五个关键步骤逐步完成教学任务：知识建构—知识整理—知识互联—知识回溯—知识内化。基于学科教学目标的主次性，在具体教学实施中物理和数学的地位并不等同，物理的跨学科融合教学目标仍是引导学生更好地掌握物理知识，而数学融合是为了更好地理解和掌握物理新知识而采用的辅助工具。教师通过发现和总结数学与物理两门学科间的潜在联系，挖掘可渗透的交叉点，在学生已完成数学知识认知和建构的基础上，将其有用部分整合运用到物理的课堂教学中，从而帮助学生更好地理解和内化物理新知识（图1）。下面以鲁科版普通高中物理选择性必修第二册第一章第2节“洛伦兹力”为例，阐述数理融合教学的模式建构及教学过程。

3    基于素养导向的目标设计

3.1    教学内容分析

洛伦兹力的应用是学生掌握洛伦兹力的表达式和方向特征之后进行的拓展研究，要求学生能够理解和运用带电粒子在磁场中运动的动力学关系，求解出相应的半径、圆心角、时间等参量；是一节融合了力学、电磁学和数学的融合性课程，考查学生在物理知识中综合应用数学知识的能力。

3.2    学情分析

学生在完成牛顿运动定律、圆周运动、动能定理、洛伦兹力的表达式和方向判断等知识的学习后，已经具备了进行深入研究的知识储备。接下来，课程将继续探讨带电粒子在洛伦兹力作用下的动力学特征，通过知识关联和专业建模推导，帮助学生顺利掌握将数学语言与物理规律精准化融合的技巧，提升数理结合的能力，引导学生应用已有基础知识，通过理论分析和推理判断来获取新知识，并分析新现象（图2）。

4    教学过程设计

4.1    知识建构——物理情境创设

依据课程目标选择合适的情境作为教学的切入点，引起学生积极关注。作为教学实施的初始环节，科学合理的情境设置可以将学生置于与现实紧密联系的场景中，有效地引导学生实现虚拟环境与现实世界的衔接，快速形成具有吸引力的焦点和跨学科主题，为后续的跨学科教学做好铺垫。情境化的教学方式可根据教学内容和教学目标灵活设定，一般有生活情境、实物情境、模拟情境、问题情境、实验情境等。本节课根据课型特点，可以采用实验情境的方式进行物理知识建构，通过视觉化、具象化的实验演示粒子在洛伦兹力作用下的运动过程，让学生在情境中回忆旧知识，应用旧知识，并主动建构新知识。

教学实施：

利用洛伦兹力演示仪（图3）进行分组实验，运用控制变量法探究洛伦兹力与磁感应强度方向、粒子速度方向的关系，完成表1。并观察粒子在洛伦兹力作用下的运动轨迹，形成“心智模型”。

通过上述控制变量实验探究，促进学生直观感知运动电荷在磁场中的运动学特征，为后续的理论推导奠定具象化基础。

4.2    知识整理——洛伦兹力动力学分析

教师对教学所需的旧知识进行梳理，与建构环节的引导知识和跨学科主题进行有效整合，提炼出与主题相关的知识点，并形成一个完整的知识链体系。在洛伦兹力这个聚焦主题的教学过程中，教师可利用圆周运动动力学、功能关系等旧知识，归纳出带电粒子在洛伦兹力作用下的运动轨迹，形成与动力学之间的关系，让学生产生新旧知识的有效衔接和认知突破，为后续的拓展研究做好铺垫。

教学实施：

教师针对知识建构环节的实验结果，推导出两条思维拓展链条，引导学生从理论上探讨实验现象，形成洛伦兹力的知识框架。

思维拓展链1——带电粒子轨迹模型的形成：

运用所学知识（牛顿运动定律和动能定理）探讨带电粒子在磁场中的运动特征，引导学生运用旧知识分析新物理现象，完成带电粒子在磁场中运动轨迹模型的建构。

引导途径：左手定则—带电粒子速度方向始终垂直于洛伦兹力—洛伦兹力永不做功—速率始终不变（动能定理）。

结论：带电粒子运动轨迹——匀速圆周运动。

思维拓展链2——带电粒子动力学问题研究：

设计意图：以力学的匀速圆周运动旧知识为源，探究带电粒子运动参量（半径R和周期T）的表达式，使学生认识不同物理表象的本源关联，深刻体会物理规律的内在统一性，建立系统的物理分析思想（旧知识—迁移—新现象）和方法意识（理想模型探究法），并为后续的数理融合教学奠定基础。

教师梳理：

qvB=m，得R=

qvB=mR，联立v=R，得T=

得出圆周运动的两个重要参量：R和T。

教师拓展：圆周运动其他参量的计算（圆心角θ、弦长L、弧长s、运动时间t等）。

（1）圆心角：利用圆的几何关系；

（2）弦长：L=2Rsin；

（3）弧长：s=Rθ；

（4）时间：由=，得t=。

核心问题提出：带电粒子运动规律的关键是描绘粒子运动的轨迹，即画轨迹圆。

4.3    知识互联——物理模型数学化

利用物体运动轨迹圆和数学圆图形描绘方法的相通性，将物理圆实体轨迹变换为数学抽象化模型，即物理模型数学化。学生利用已熟练掌握的画圆方法，找出确定圆的核心要素——位置、半径和切线，引导学生从数学视角探索出画轨迹圆的条件，利用数学组合思维建构出试题可能承载的轨迹类型，再进行物理移植和外包形成一个系统可衔接的跨学科矩阵构架。

知识互联环节：通过数学语言描述，运用数学思维建构模型解决后续的物理问题，让学生学会从已学习的其他学科旧知识延伸应用到物理新问题上，了解数学学科和物理学科间关联的本质内涵，从而达到明晰知识内涵、完成知识迁移的目的［5］。

数学知识梳理：复习数学画圆的相关知识，引导学生在数学抽象情境中探究可能的轨迹模型。

命题提出：已知圆轨迹的A、B、C三个点，请绘制出过三个点的轨迹圆？

描绘策略：过其中两点作弦及其中垂线，交点即为圆心，圆心与点的距离即为轨迹半径（图4）。

轨迹类型拓展：教师以命题条件设计为问题中心展开课堂讨论，引导学生从试题编制的视角归纳轨迹圆的可能类型，加深对模型命题和解题的认识，学会从模型入手分析问题的方法，实现知识体系的自主建构。

教师对学生讨论总结得出的画轨迹圆条件进行归类汇总，整理出可能的命题类型，完成数学模型的建构（表2）。

4.4    知识回溯——移植教学范式

知识回溯的目的是实现物理情境回归，以完成源于物理、延伸于数学、最终回归物理的教学闭环设计。将归纳出的数学轨迹模型进行等价移植回归，得出粒子运动轨迹的可能命题及描绘方法，建构物理模型。移植教学基于物理、数学学科间的知识衔接，在两门学科间进行移植和转换，从而使学生更容易得出物理的可能情境和模型，形成物理新知识模块，从而完成两门学科知识的衔接和物理模型的建构。

知识移植：教师将数学概念中的轨迹圆与带电粒子在磁场中运动的轨迹进行横向对比，得出确定粒子轨迹圆的关键要素——位置、半径和粒子的速度方向（图5）。

教师评估数学模型的运算结果，回归物理课堂教学，展示粒子运动轨迹类型。

情境1：已知带电粒子运动轨迹上的三个位置（设为A、B、C），确定粒子的运动轨迹［6］。

轨迹描绘：

参照数学模型“已知圆上的三个点”轨迹的描绘思路确定粒子运动轨迹的圆心和半径（图6）。

情境2：已知带电粒子运动经过的两个位置（设为A、B）和其中一个位置（设为A）的速度方向［6］。

轨迹描绘：

移植“已知两个点和其中一个点的切线”的数学模型，点对应于粒子的两个位置，切线对应于位置A的速度方向，得到情境2的运动轨迹的确定方法（图7）。

情境3：已知带电粒子运动经过的某个位置及该位置的速度方向（已知位置设为A）、在其他位置时的速度方向（位置未知）［6］。

轨迹描绘：

速度方向对应为数学轨迹圆的切线，实现“已知一个点及两条切线，其中一条切线过已知点”数学轨迹描绘方法的物理移植，得出情境3的轨迹确定方法。速度方向延长线的交点的角平分线与已经位置速度方向垂线的交点即为轨迹圆的圆心（图8）。

教师提出问题：除了上述三种情境类型以外，还能归纳出几种基于数学模型的物理情境？

设计意图：通过对轨迹情境类型的分析，检验学生从数学几何学和组合学角度探索物理轨迹的能力，建构出轨迹问题的知识结构框架，培养学生数理融合的跨学科能力和科学思维与科学探究两个维度的学科素养。

4.5    知识内化——情境模型应用

知识内化的环节设计是为了提升学生运用整理归纳的物理模型解决新问题的能力。学生运用建构的数理模型，给予一定的物理外包，再转换不同的问题情境，让学生学会从不同的问题表象中找相似的解决方法，实现知识内容体系的归一化，逐步建构新知识的结构框架，丰富跨学科教学内容，完善教学流程，培育学科融合分析能力。

典例1 如图9所示，一垂直纸面向里的匀强磁场存在于正六边形区域内。一粒子从a点沿ad方向以速率v1射入正六边形区域内，从c点射出磁场；若该粒子从a点沿ae方向以速率v2射入该区域内，恰好从d点射出磁场［7］。不计粒子重力，则的值为（      ）