基于三种表征的高中生运动学概念理解情况调查研究

收稿日期：2023-11-18

基金项目：河南省2021年度教师教育课程改革研究重点项目“基于案例研究培养物理教师科学思维教学与评价能力”（2021-JSJYZD-012）。

作者简介：刘佳萌（2000-），女，硕士研究生，从事物理课程与教学论研究。

摘   要：以新乡市某中学120名高中生为研究对象，以运动学概念测试（KCT）为研究工具，基于三种表征方式测查高中生对于高中物理运动学部分的掌握情况。调查发现，学生对运动学部分的整体掌握情况较好，存在的问题主要是：对加速度的理解存在误区；从运动图中提取信息能力较弱；不易将数学知识迁移到运动学问题的解决过程之中。据此对中学物理教学提出了对应建议。

关键词：概念理解；物理教学；运动学；表征方式

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2024）3-0087-5

在物理教学中，经常用到三种直观表征物体运动特点和规律的方式：图片、表格和曲线图，这些内容涉及到较多的数学知识，反映了物理学以数学为工具的特点。《普通高中物理课程标准（２０１７年版）》中，明确提出要注重表达形式：包括文字、表格、图像等［１］。近年来，高考对多种表征方式的考查也日渐重视，教育部考试中心建议：“通过文字、图形、表格等方式呈现试题，考查学生从多种形式的呈现材料中筛选、分类、归纳、整合相关信息，提取有效信息，构建物理图景，分析物理过程，解决物理问题的能力。”［２］

已有研究指出，在某种表征中理解了一个概念的学生很难将这个概念转移到另一种表征中类似的问题上［３］。运动学部分是物理课程的基础，虽然大多数力学概念测验都包含了运动学的内容，但是系统探索不同表征方式下基本运动学概念的概念测验仍然缺乏。

本研究基于三种表征方式测查学生对于运动学部分的掌握情况，帮助教师了解高中生运动学知识的学习情况，并对教师的教学方式、双减背景下的作业设计与习题训练提出针对性的建议。

1    研究方法

1．１    研究对象

对新乡市某中学高一学生发放１３２份试卷，回收有效试卷１２０份。正式施测时间是２０２３年６月，此时被测对象处于高一下学期，已经完成了高中物理课程中运动学模块的学习。

1．２    研究工具

本研究采用测验法和访谈法，测试工具为经过翻译和本土化改写的“运动学概念测试”（Ｋｉｎｅｍａｔｉｃｓ Ｃｏｎｃｅｐｔ Ｔｅｓｔ，简称ＫＣＴ）。ＫＣＴ是苏黎世联邦理工学院的Ｌｉｃｈｔｅｎｂｅｒｇｅｒ、Ｗａｇｎｅｒ等开发的测试，由４９个单项选择题组成。该测试在考查运动学知识的同时，还突出了表征方式与数学知识对学生解决运动学问题的影响。相较于传统的运动学测试题，该测试更能检测出学生对速度、加速度、位移等描述运动的几个基本物理量的深刻理解。

三种表征方式指图片、表格和曲线图。七个基本运动学概念包括：速度作为比率、速度作为一维向量、二维速度的叠加、位移为ｖ－ｔ图中的曲线下面积、加速度作为比率、加速度作为一维向量、速度变化量为ａ－ｔ图中的曲线下面积。涉及到的三个基本数学概念指斜率、向量和曲线下面积。

对本测试量表的信度分析主要通过将本次测试数据录入到ＳＰＳＳ２６．０软件中，得出Ｃｒｏｎｂａｃｈ＇ｓ ａｌｐｈａ系数为０．８９５，在０．８０和０．９０之间，表明该测试卷的内部一致性较高，是一个同质性信度比较好的测试工具。

2    调查结果

2．１    学生总体水平

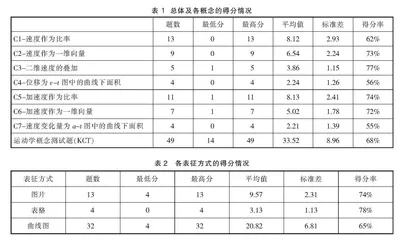
探讨全体学生总体及各概念的表现情况，如表１所示。从总体上看，该测试题得分的平均值为３３．５２，整体得分率为６８％，学生对于运动学概念的知识掌握处于及格水平，说明学生对于运动学概念整体掌握情况不错。其中，在“速度变化量为ａ－ｔ图中的曲线下面积”“位移为ｖ－ｔ图中的曲线下面积”两个维度的表现情况最差；在“二维速度的叠加”维度中学生的表现情况最好。

探讨各表征方式的表现情况，结果如表２所示。以得分率为标准，排列出全体学生在三种表征方式的表现，由优至差依次为：表格、图片、曲线图。其中，表格表征的得分率最高，达到７８％，处于中等水平；曲线图表征的得分率最低，为６５％，处于及格水平。综上所述，在运动学概念测试题中，学生对于不同表征方式的表现情况有差异。其中，对于表格表征的问题，学生掌握情况最好，图片表征次之，学生对于曲线图表征方式掌握的情况弱于前两者。说明即便考查相同概念，学生解决不同表征方式问题的能力是不同的。

2．２    学生存在的问题与原因分析

由上述可知，学生整体对运动学部分的掌握情况不错。但根据答题情况并结合访谈发现学生学习中仍然存在一些问题，下面将从学生对物理概念的理解、信息提取与转换以及用数学知识解决物理问题三个方面进行讨论。

（１）学生对加速度的理解存在误区：把速度的增减与加速度的正负相联系；把加速度的变化与速度的变化相联系。

如图１题目所示，当ａ为恒定负值时，多数学生认为第一段是匀减速运动，并认为“ａ为负值，ｖ减小”，且给出判断加速度方向的依据是“看速度增大或是减小”“加速度为正，速度越来越大；加速度为负，速度越来越小”。由此可见，学生潜意识里将速度的增减与加速度的正负相联系，在看到加速度为恒定负值时便默认为该运动是匀减速运动，而忽略了实际有两种情况：正方向的匀减速运动和反方向的匀加速运动。出现此类问题的原因可能是学生只是记住了加速度方向与Δv的方向相同，没有规定初速度方向的意识，没有结合作图的方式对初速度方向的两种情况进行理解。

■

图 １  题目１９示意图

学生对加速度理解的另一个误区是：将加速度的变化与速度的变化量相联系。如图２所示，在给定ａ－ｔ图像中比较速度变化量大小时，许多学生选择（d）选项，给出的判断依据是“加速度变化越大，速度的变化量越大”。可见，学生在分析本题时将加速度变化与速度变化量看作是一致的，说明其对加速度的概念及其物理意义的理解比较模糊。造成这类问题的原因可能是学生只是单纯地对加速度公式进行了简单记忆，而对公式中各物理量所表示的定义与所表达的物理意义并没有确切理解。当速度变化量与加速度同时出现时，学生会由于本身对概念的不理解或混淆概念导致题目的错误解答。

■

图 ２  题目２２示意图

（２）学生从运动图（频闪图片）提取有关信息的能力弱于表格

在表格表征时学生可以准确读出Δｘ或Δｖ，在考查同概念的运动图类问题中，学生会受干扰无法读出图片中的有关Δｘ或Δｖ。如图３所示，许多学生选择Ｂ选项，给出的判断依据是“两个小人重合了”“第５ ｓ时，时间和位移相同，故速度相同”。上述理由说明学生没有从运动图中读出相邻时间间隔的位移或者学生不知道要从图中读取信息。在访谈过程中，若将图中的信息转化为表格呈现给学生，大部分学生可以正确作答。因此，学生并非完全不会这些题，而是从图中提取信息时出现了困难，他们难以从图中读出解题所用的正确数据。

表格呈现出的是直观的物理数据，图片呈现出来的贴近运动情境，更接近现象本身。出现上述情况的原因可能是学生平时训练时接触的公式题、概念题较多，这些题型直接将数据提供给学生，学生只需要根据已有概念判断或运用公式去计算即可。这类题目对物理公式、概念进行了考查，但没有让学生自己经历信息提取与转换的过程。由于学生缺乏对于数据提取的训练，因此，即便是考查相同概念，解决图片表征问题的能力会弱于表格表征。

■

图 ３  题目２５示意图

（３）学生不易将数学知识迁移到运动学问题的解决过程之中

向量在物理学中叫作矢量，在矢量叠加问题中学生出现的困难有：在二维速度叠加时没有想到用平行四边形定则；使用平行四边形定则后不会用三角形的边角关系去判断合速度的取值范围；将平行四边形定则与正交分解法混淆等。

学生习惯用物理思维或生活经验判断矢量叠加问题。如图４所示，其判断依据有：“箭速度不受马影响，考虑空气阻力应小于初速度”“在马上射箭不影响箭的速度”“马以１０ ｍ/ｓ的速度运动，箭带着马的惯性运动”。可见，这些学生在解决问题时没有用平行四边形定则，他们更倾向于用经验的方式去判断问题，没有将其转化为数学问题。在访谈过程中发现，也有学生作出平行四边形后不会根据三角形的边角关系去判断合速度的取值范围，可见其对于数学知识在物理方面的运用并不熟练。此外，也有学生把平行四边形定则叫作“正交分解法”，说明学生对于物理学中的一些方法并不完全熟悉。

■

图 ４  题目8示意图

学生在斜率问题中出现的困难有：区间点混淆，即求斜率时将坐标轴上的一个坐标点代入；认为斜率为正的曲线上某点的速度大于斜率为负的曲线上某点的速度。

如图５所示，学生选择的大多数为Ｃ选项，并给出如下判断依据：“代入在ｔ＝２ ｓ时的一个点”。通过访谈发现，学生知道ｘ－ｔ图像的斜率表示速度以及速度的计算公式。即便掌握基本的公式以及在x-t图中斜率表示速度，学生还是会在曲线图中求速度的问题中出现错误，说明学生潜意识里对于斜率本身的计算方式不熟悉，或者没有将曲线图中的斜率作为物理量来计算，而是用自己错误理解的物理方式去计算。

■

图5  题目16示意图

在同一图像中比较速度大小时，学生会认为曲线上斜率为正的某点的速度大于曲线上斜率为负的某点的速度。例如图６，学生在ｘ－ｔ图像中比较以下几点速度大小时，选择Ｂ选项和Ｃ选项较多。通过访谈发现，学生在判断时更关注正斜率，而将负斜率默认为比较小，说明学生对矢量的正负表示方向的意识不清晰。

■

图6  题目11示意图

学生关于曲线下面积问题中的困难有：解题中不会运用曲线下面积，而是通过读出坐标轴上的点构建错误的物理公式解决；对于曲线下面积的理解模糊，构建错误的面积。

在ａ－ｔ图像中比较速度变化量时，只有极个别学生会用曲线下面积判断速度的变化量。同样在ｖ－ｔ图像中求位移时，部分学生也会忽略用曲线下面积作判断，他们会选择在曲线图中去寻找相关物理量，再试图用物理公式去计算。例如图７，部分学生会分别读出物体在ｔ＝１ ｓ与ｔ＝５ ｓ时的速度，接着将数据代入一个物理公式中求出位移，但通常会选取错误的公式。

■

图 7  题目35示意图

除此之外，有学生用曲线下面积去解答，但选择了错误选项Ｃ，这部分学生中存在共同的问题：他们构建出了同一类错误面积。如图８所示，通过访谈发现他们在构建面积时在ｖ＝６ ｍ/ｓ处画了一条水平线，于是便构建出图中由斜线所示的三角形。他们所求的就是这个“三角形”的面积，而非与ｘ轴所围成的“梯形”面积。同样的错误在类似的另一道面积题中也出现过，如图９所示。说明学生对于曲线下面积的理解比较模糊，即使知道曲线下面积所代表的物理意义，但在构建曲线下面积时也会出现问题。

■

图 8  学生构建的错误面积示例一

■

图 9  学生构建的错误面积示例二

综上所述，即使用数学方法解决问题更加简单直观，学生还是会偏向于用物理或经验方式来解决问题。对学生来说，也许将物理问题转化为数学问题并不是一件容易的事情，造成此类问题的原因可能如下：第一，学生本身的数学知识比较薄弱，其数学基础不足以去解决所面对的问题；第二，在解题时没有将物理模型转化为数学模型的意识。