跨学科背景下高中生物理模型建构能力测评研究

摘   要：“模型建构”是物理学科核心素养中“科学思维”的关键要素之一。发展模型思维，提升学生运用物理模型解决跨学科问题的综合能力，为人才培养提供了有效手段。以跨学科背景中物理建模能力为核心，归纳已有研究的评价要素，建构了测评框架。命制了跨学科情境的物理建模测试题，以１２５名广州市高中学生为研究对象，实施纸笔测验。基于Ｒａｓｃｈ模型对数据进行统计分析，揭示了高中生跨学科背景中物理建模能力的现状与特点，以改进一线教学。

关键词：物理建模能力；跨学科；测评；Ｒａｓｃｈ模型；高中生

中图分类号：G633.7 文献标识码：A    文章编号：1003-6148（2024）8-0088-5

新课程改革要求学生不局限于理解科学，还应具备跨学科的知识与能力。“跨学科实践”已被纳入《义务教育物理课程标准（２０２２年版）》之中［１］。在课标的指引下，一系列与跨学科相关的主题学习活动、课程设计和评价实践等正蓬勃发展。“模型建构”是《普通高中物理课程标准（2017年版2020年修订）》核心素养中“科学思维”的关键要素之一［２］，它关乎学生能否将真实问题中的对象和过程进行抽象表征，是一种重要的思维能力，与学生解决跨学科问题的水平密切相关。当前，国内外研究者们基于跨学科视角开展测评，但多数聚焦于单个主题［３–５］，针对物理建模能力的研究，也较少要求学生将模型运用到跨学科情境之中［６–８］。

针对上述研究的不足，本文拟研究高中学生跨学科背景中物理建模能力水平。从组成上来看，该能力由“跨学科”和“物理建模”两个要素复合，它是指学生从跨学科背景中提取信息，分析研究对象的主要特征，建构适当的物理模型并通过模型解决相应问题的能力。本研究尝试在已有物理建模理论和跨学科情境试题的基础上，编制出适用于高中学生群体的跨学科背景中物理建模能力测试卷，分析该能力与学生学业成就之间的关联，探寻影响学生解决跨学科情境问题能力的重要因素，提供科学有效的测评工具。

１    研究方法

１．１    建构测评框架

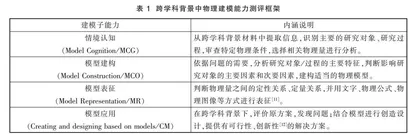
自以Ｈｅｓｔｅｎｅｓ和Ｈａｌｌｏｕｎ为代表的学者提出科学建模教学的概念开始［９-１０］，已有许多研究者从要素取向、认知取向、行为取向等不同角度提出物理建模理论，开发相应测评量表。Ｈａｌｌｏｕｎ创立了科学建模过程模式理论［10］，将基于问题解决的建模细分为五个环节：模型选择、模型建构、模型验证、模型分析和模型拓展，该模式在物理建模的相关研究中得到广泛借鉴与引用。本研究以Ｈａｌｌｏｕｎ科学建模过程模式理论作为基础，提取四个物理建模子能力，并结合跨学科的要素，制订跨学科背景中物理建模能力测评框架（表 １）。学生运用物理模型解决跨学科问题，需经历情境认知—建构模型—表征模型—应用模型的思维过程。

第一，跨学科背景试题中的信息需要被提取与整合，这一过程指向情境认知能力（Ｍｏｄｅｌ Ｃｏｇｎｉｔｉｏｎ，以下简称ＭＣＧ）。被试要识别研究对象，推断哪些属性应该被忽略，哪些应该被包括在模型中，其完成度将会影响后续建构模型的准确性。此外，“Model Cognition”的直译为“模型认知”，结合该子能力的内涵以及具体语境，笔者在此将其译为“情境认知”。第二，在整合信息的基础上，通过抽象、理想化、简化和近似等研究方法，将复杂实际问题中的对象和过程转换成物理模型，对应模型建构能力（Ｍｏｄｅｌ Ｃｏｎｓｔｒｕｃｔｉｏｎ，以下简称ＭＣＯ）。第三，将物理模型用文字、图像等形式进行表征，兼顾定性与定量特点，对应模型表征能力（Ｍｏｄｅｌ Ｒｅｐｒｅｓｅｎｔａｔｉｏｎ，以下简称ＭＲ）。第四，将模型应用到跨学科情境中，进行评价、改进与创造设计等，解决真实问题，对应模型应用能力（Ｃｒｅａｔｉｎｇ ａｎｄ ｄｅｓｉｇｎｉｎｇ ｂａｓｅｄ ｏｎ ｍｏｄｅｌｓ，以下简称ＣＭ）。

１．２    开发测评工具

基于上述测评框架，选择了历史、生物、地理和工程技术作为跨学科背景开发测评工具。以火药、风力发电等真实情境作为素材，所有试题均以原始物理问题的形式呈现，表2简单描述了试题情境与要求。与传统习题相比，原始物理问题中的数据或条件是隐藏的，与真实情境更为契合［１３］。测试卷共设四道建构反应题，各题依据学生的作答情况对四个建模子能力维度分别进行赋分。

以第一题为例，题干中部分信息如下：“该‘礼花弹’设计精妙，由发射筒、引线、礼花弹、发射药、延期引线等构成。礼花弹从地面沿竖直方向射出，由于延期引线的存在，礼花弹上升到最高点时才炸开。请用物理知识分析礼花弹的运动过程……”。对于此题的作答，被试应识别研究对象，判断礼花弹做竖直上抛运动（情境认知）；发射药引爆后，礼花弹以一定的初速度做竖直上抛，同时延期引线开始燃烧，当上升到最高点时延期引线正好燃尽，礼花弹在最高点炸开。据此，可建立延期引线的长度与飞升时长的关系（模型建构）；题目未预设物理量，学生应主动完成赋值表征，并结合物理图像等方式描述礼花弹的运动（模型表征）；改进礼花弹的结构，自主设计方案（模型应用）。

为了进一步对考查进行量化，四道建构反应题拟定了评分标准，被试各题情境认知、模型建构、模型表征和模型应用的得分被划为０～３四级水平。题中涉及到的物理知识与被试的知识水平相适应，难度适中。

１．３    研究对象、施测方法与统计工具

测评卷涉及的物理知识以力学和运动学为主，对应的学段为高中一年级。在正式施测前，进行了小样本初测。统计发现，T2与T3试题的平均难度最为接近，因此在大规模测验中采用划分A、B卷的形式，将T2、T3试题各自作为A、B卷的不同题目。正式测验时，选择了广州市荔湾区某中学高一年级四个平行班的学生作为研究样本，于自修课时间段（４５分钟）开展了纸笔测验。回收测试卷共１５４份，经统计，有效测试卷为１２５份，有效率８１．２％。其中，男生样本６２份，女生样本６３份，性别分布较均衡。本研究基于Ｒａｓｃｈ模型进行数据处理，使用Ｗｉｎｓｔｅｐ软件及ＳＰＳＳ２５．０完成数据分析。

２    测试工具质量检验

２．１    与Ｒａｓｃｈ模型拟合度

Ｗｉｎｓｔｅｐ软件报告了信度、拟合度等总体情况。结果显示，本次测验项目信度为０．９５，被试信度为０．７５，测试结果较为稳定、可靠。测验项目内部拟合度、测验被试内部拟合度Ｉｎｆｉｔ ＭＮＳＱ均为１．００，各项目内部拟合度均在 ０．８～１．４ 之间，数据结果与Ｒａｓｃｈ模型拟合度高［１４］，适合采用Ｒａｓｃｈ模型进行分析。

２．２    项目难度与误差、怀特图

测验被试难度值Ｐｅｒｓｏｎ Ｍｅａｓｕｒｅ＝－０．７，接近０，但小于０，整体的试题难度与被试能力较匹配，但难度略高于被试能力，符合预期。各项目难度Ｉｔｅｍ Ｍｅａｓｕｒｅ范围在－１．０１～１．１０之间，跨度近似为２．０，分布在合理的区间。项目标准误差（Ｍｏｄｅｌ Ｓ．Ｅ．）在 ０．１０～０．１６ 之间，测量精确性较好。各项目点测量相关系数都大于 ０．３。怀特图显示了被试水平和项目难度在同一客观等距量尺上的ｌｏｇｉｔ值，如图 １所示。

其中，能力值处在中间水平ｌｏｇｉｔ ＝ ０的被试最多，被试能力整体呈现正态分布；同时，分布连贯、不同难度的项目都有被试与之对应，总体上看，被试的能力值与项目难度匹配。以上检验结果表明，测评工具质量较好，符合Ｒａｓｃｈ模型的要求。

３    研究结果分析

３．１    跨学科背景中物理建模能力与学业成就的关联

通过数据可以探究学生跨学科背景中物理建模能力与其学业成就之间的关联。经统计，测评ｌｏｇｉｔ分与学生诊断性测验物理成绩的相关性的显著性概率ｐ＝０．０３８＜０．０５，且皮尔逊相关系数ｒ ＝ ０．１８６＞０，二者有统计意义上的正相关性。从逻辑上分析，跨学科背景中物理建模能力与学生本身的物理基础存在一定的关联，其中，抓住主要因素进行建模、采用物理量、公式、图像进行表征的能力在日常学习中得到了一定的培养。上述结果分析表明，立足于物理学科，学好基本知识和思维方法，是学生成功“跨”出学科的前提。

值得注意的是，相关性在不同维度上的表现有所不同（表 ３）。其中，情境认知与模型建构两个维度ｌｏｇｉｔ分与学业成就有显著的相关性。而模型表征和模型应用能力与学生的学业成就没有统计意义上的相关性。

结合学生作答个案发现，物理基础扎实的学生往往在认知、建构和表征维度表现较优，但未必能很好地将模型运用于跨学科情境中，这需要学生具备一定的迁移、应用与创新能力。由此可见，当前的物理教学对培养学生认知情境、建构模型和表征模型的能力有较好的促进作用，但在发散思维、情境迁移和创新能力等方面有待加强。

３．２    物理建模子能力之间的关联

为进一步探究学生的思维过程，分析了各子能力间的相关性。结果显示，情境认知与模型建构（ｒ ＝ ０．７３４）、模型建构与模型表征（ｒ ＝ ０．７２８），这两对变量之间存在显著的强相关性。

首先，情境认知完整与否将影响模型建构能力。情境认知需要学生从复杂真实的问题情境中提炼关键信息、厘清题意并审查物理条件。这是建模的重要环节，它是个体为建模而先生成的认知结构，情境认知的完成度会影响模型建构的准确性。其次，模型建构与模型表征之间也存在密切的联系。对比发现，如果学生建构的模型比较完整，那么表征方式往往会更加多元。建模水平高的学生能通过选取合适的方法将对象和过程转换成物理模型；而建模水平较低的学生，对模型的认识比较浅，仍处在具象思维到抽象思维的过渡阶段。前者能够采用文字表征、赋值表征、图像表征等多种方式将抽象的模型进行表达；后者的表征形式则较为单一，表征转换能力较弱。

从呈现方式来看，物理概念与规律总是以各种外部表征为载体。建构准确的物理模型可以促进学生使用多元表征，多元表征也可以反过来检查模型间的一致性，用一种表征来帮助建构另外一种表征［１５］。

３．３    学生建模子能力的整体表现

将测试卷的各项目按维度进行分类，对比学生在认知、建构、表征和应用的表现情况，如图 ２所示（各维度的平均难度用菱形标记折线表示）。难度值可以反映学生的作答情况，其中，情境认知维度平均难度最小，学生的表现相对最好，模型建构维度平均难度最大，学生的表现相对最弱。

情境认知是建构模型的第一步。情境为学生提供了认知的起点和关联的信息与条件，试题中的条件是内隐的，学生需要调用自身掌握的知识，提炼跨学科背景中蕴含的物理条件，为下一步的模型建构作准备。研究发现，除了小部分学生出现遗漏、曲解物理条件的情况外，大部分学生能够基本达到情境认知维度的要求，整体表现较好。

模型建构是整个物理建模流程的核心。基于已有的知识结构和情境问题建构物理模型的抽象概括过程，是科学思维的重要体现［１６］。对于部分学生而言，模型建构是具有挑战性的。一方面，学生可能对基本的物理模型知识储备不足；另一方面，学生难以在跨学科情境下将模型重新组合，未能通过抽象、理想化和简化近似等方法将跨学科中的物理过程与已知的物理模型联系起来。学生在这一维度的表现差异较为明显，整体表现相对最弱。为了提升学生的模型建构能力，需要完善学生对基本物理模型的认识，加深对真实情境中物理现象的思考，培养从情境到模型的思维能力。

３．４    跨学科背景对物理建模能力的影响

测试卷中有四个不同的跨学科情境：历史、生物、地理和工程技术。图 ３展示了不同情境对项目难度的影响。在不同学科背景下，学生情境认知和模型应用的能力水平相对稳定。而模型建构和模型表征能力受到问题情境的影响较大，波动明显。试题中不同的学科背景会影响学生的建模表现，而表征和建构两个维度关系密切，因此它们受到跨学科背景的影响更加显著。