一道经典高考试题的深度思考与拓展

摘   要：２０１８年江苏卷物理第２２题涉及两个物体的关联运动。利用余弦定理和正弦定理确定两物体动能与角度的关系，并用ＧｅｏＧｅｂｒａ软件作出其图像。尽管两物体动能都是先变大后变小，但两者不是同时达到动能的最大值。

关键词：高考试题；拓展思考；ＧｅｏＧｅｂｒａ软件

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2023）12-0042-3

高考压轴试题对学生的思维能力要求高。如何突破压轴试题的思维难点，提升学生解决问题的思维能力层次，是高三备考的关键。本文以一道经典的高考试题——２０１８年江苏卷物理第２２题为例，借助ＧｅｏＧｅｂｒａ软件，对试题进行拓展和延伸，直观呈现物体运动过程和状态细节，使学生思维从关联结构向拓展抽象结构能力层次发展。

１    试题呈现

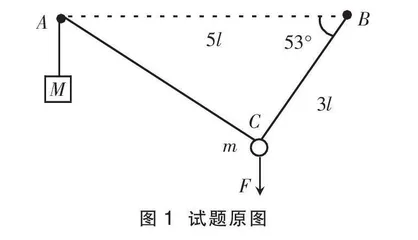
例１ 如图1所示，钉子Ａ，Ｂ相距５ｌ，处于同一高度。细线的一端系有质量为Ｍ的小物块，另一端绕过Ａ固定于Ｂ。质量为ｍ的小球固定在细线上Ｃ点，Ｂ，Ｃ间的线长为３ｌ。用手竖直向下拉住小球，使小球和物块都静止，此时ＢＣ与水平方向的夹角为５３°。松手后，小球运动到与Ａ，Ｂ相同高度时的速度恰好为零，然后向下运动。忽略一切摩擦，重力加速度为ｇ，取ｓｉｎ５３°＝０．８，ｃｏｓ５３°＝０．６。求：

（１）小球受到手的拉力大小Ｆ；

（２）物块和小球的质量之比Ｍ：ｍ；

（３）小球向下运动到最低点时，物块所受的拉力大小Ｔ。

评析：问题（１）的思维能力层次要求为多点结构。学生需要正确分析小球的受力，并利用力的合成和分解的知识建立方程，求解拉力大小。问题（２）为弱关联结构。学生需要从运动的角度理解小球和物块的速度均为先增大后减小。当小球处于高度ＡＢ时，小球和物块的速度均为零。学生还需要从做功的角度判断系统在运动过程中机械能守恒，并根据能量守恒定律列出相应的方程。问题（３）属于强关联结构。学生需要知道小球运动到最低点时，小球和物块的速度为零，两细绳垂直，夹角为９０°。物块的加速度和小球的切向加速度大小相等，小球的向心加速度为零。学生需要利用牛顿第二定律分别对小球和物块列出方程并求解［１］。

解析 （１）由于ＢＣ＝３ｌ，ＡＢ＝５ｌ，故ＡＣ＝４ｌ，∠ＡＣＢ＝９０°。小球和小物块均平衡，绳子ＡＣ拉力大小为Ｍｇ，绳子ＢＣ拉力为Ｆ１。对小球分析，把重力分解到两绳方向，有F1=（mg+F）sin53°，Mg=（mg+F）cos53°，解得F=Mg-mg。（２）小球运动到与ＡＢ等高过程，由机械能守恒定律，有mg×3lsin53°=Mg（4l+3l-5l），解得=。（３）由机械能守恒定律可知，小球回到Ｃ点速度为零。此时切向加速度为ａ，由牛顿第二定律有Mg-T=Ma，T-mgcos53°=ma，得T=Mg。

２    运动分析

小球和物块在运动过程中的最大动能分别是多少？它们的动能是否同时达到最大呢？

利用速度关联确定物块与小球的速度关系，利用余弦定理和正弦定理确定物块和小球的位置关系，通过能量守恒定律求解物块和小球的动能和角度的关系，并用ＧｅｏＧｅｂｒａ软件作出小球和物块的动能和角度的图像，直观地呈现出关联物体的运动特点。确定两物体不是同时达到动能的最大值，由此打破学生的思维定式，培养学生的思维能力［２］。

２．１    小球动能与角度的关系

为了简单，设ｍ＝２ ｋｇ，Ｍ＝２．４ ｋｇ，ｇ＝１０ ｍ／ｓ２。当∠ＡＢＣ＝θ时，小球速度为ｖ１，ｖ１与绳ＡＣ的夹角为α，物块速度为ｖ2，绳ＡＣ长度为ｘ，如图2所示。由余弦定理可知，x=l。

由正弦定理有=，可以求得cosα=。由速度关联的特点可以得出v2=v1cosα。

小球和物块在运动过程中机械能守恒

Mg（4l-x）-3mgl（sin53°-sinθ）=mv+Mv

代入上述相关关系及数据，可以得到

mv=

10×l（J）

利用ＧｅｏＧｅｂｒａ软件，作小球动能和角度的关系图像（图３）。可知，当角度θ＝０．２６ rad，即θ＝１４．９°时，小球动能达到最大值６．９６ Ｊ。当角度０．２６ rad≤θ≤０．９２ rad，即１４．９°≤θ≤５３°时，随着角度变小，小球动能越来越大。当角度０ rad≤θ≤０．２６ rad，即０°≤θ≤１４．９°时，随着角度变小，小球动能越来越小。

２．２    物块动能与角度的关系

由上述关系可以同时求出物块动能和角度的关系

Mv=

l（J）

利用ＧｅｏＧｅｂｒａ软件，作物块动能和角度的关系图像（图４）。当角度θ＝０．５ rad，即θ＝２８．６６°时，物块动能达到最大值４．８７ Ｊ。

对比图３和图４，小球从最低点释放后向上运动过程中，小球和物块不会同时达到最大动能。物块先达到最大动能，然后小球达到最大动能。

３    平衡分析

改变试题条件，对试题进行变化，有利于我们从不同角度理解物理模型，丰富物理模型的情境，增强学生解决实际问题的能力，提升学生思维的灵活性和开放性。

如图５（１）所示，保持小球质量ｍ不变，改变物块质量Ｍ，使系统平衡。设绳ＡＢ长度为ｌ，绳ＢＣ长度为ｌ１、与竖直方向的夹角为α，绳ＡＣ长度为ｘ、与竖直方向的夹角为β。分析绳ＢＣ的拉力Ｆ、物块质量Ｍ分别与夹角α的关系。

小球受力分析图如图５（２）所示。力的平衡三角形中，由正弦定理得==。几何三角形中，由正弦定理得==，由余弦定理得x2=l2+l-2ll1sinα。

从上述三个方程可以解得

F=mg（-tanα）

M=mtanα

为理解方便，设ｍ＝０．１ ｋｇ，ｌ１＝０．５ｌ，ｇ＝１０ ｍ／ｓ２，０≤α≤９０°。利用ＧｅｏＧｅｂｒａ软件，作Ｍ－α图像和

Ｆ－α图像如图６和图７所示。

由图６可以看出，随着角度α的增加，物块质量Ｍ先增加缓慢，然后增加很快。

由图７可以看出，随着角度α的增加，绳ＢＣ的拉力先减小然后增加。由=mg（-）＝０可以得出，当sinα=时，绳ＢＣ的拉力Ｆ取极小值，此时ＡＣ垂直ＢＣ。

参考文献：

［１］王较过，赵欢苗． ＳＯＬＯ分类理论在物理教学设计中的应用［Ｊ］． 当代教师教育，２０１２，５（１）：５７-６２.

［２］左金辉，沈文炳． 一道高考选择题的思考与拓展［Ｊ］．物理教学探讨，２０１９，３７（１０）：４０-４１.

（栏目编辑    陈  洁）