多角度分析２０２３年江苏高考物理卷第１０题

摘   要：“抛体运动”“运动分解与应用”是高考常见题型，自新课改以来的三年，此类题型为江苏卷每年的必考内容。

关键词：抛体运动；运动的分解；高考试题

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2023）12-0044-3

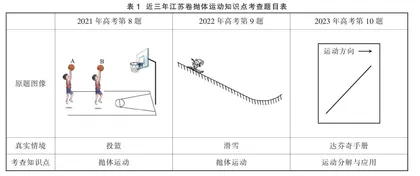
江苏卷在新课改以后考查的“抛体运动”“运动分解与应用”类题型具体如表１所示。本文着重分析江苏省２０２３年高考物理第１０题，致力于做到“一题多解”，帮助各类学生找到适合自己的解题策略。而教学中教师也要注意设置“脚踏点”，逐步加深思维深度与广度，提升学生综合能力，从而形成高阶思维［１］。

１    真题展示

达·芬奇的手稿中描述了这样一个实验：一个罐子在空中沿水平直线向右做匀加速运动，沿途连续漏出沙子。若不计空气阻力，则下列图中能反映空中沙子排列的几何图形是（  ）

１．１    方法一：作图法

取特殊值，沿水平方向、竖直方向分解运动，描点绘图。取水平方向初速度为０，加速度也为ｇ，间隔１ ｓ漏出一粒沙，根据表２展示的数据描点画出图1，得出答案。

主要公式：

y=gt2

x=at2

x=vt

１．２    方法二：数学解析法

设罐子水平初速度为ｖ０，每隔Δｔ漏出一粒沙子，观察时罐子向右运动总时间为ｔ，向右运动距离为Ｘ。

如图２逆向思考，以最后恰好漏出的沙子为起始点，研究倒数第（ｎ＋１）个漏出的沙粒

竖直方向：自由下落时间为nΔt，则

y=gn2Δt2

水平方向：匀加速时间为t-nΔt，则

x1=v0（t-nΔt）+a（t-nΔt）2

匀速时间为nΔt，则

x2=v1nΔt=[v0+a（t-nΔt）]nΔt

又x=X-x1-x2，X=v0t+at2

则x=an2Δt2

以最后恰好漏出的沙子为原点向下、向左建立直角坐标系ｘOｙ（图３）。

得=是定值，因为时间ｔ为任意值，所以所有的沙粒与最后一粒沙的连线都在一条直线上。

１．３    方法三：相对运动法

如图４所示，以最后恰好漏出的沙子为参照系，设观察时前面的某个沙粒是以初速度ｖ０水平抛出，在空中运动时间为ｔ。

竖直方向：Δy=gt2

水平方向：x2=v0t+at2，x1=v0t，则Δx=at2

得=是定值，同方法二的分析得出所有沙粒在空中在一条直线上。

２    拓  展

若利用频闪相机对以上罐子进行拍照，将会留下什么样的照片？

答案：如图５所示。

３    结  语

维果斯基的“最近发展区理论”指出，学生现有水平和可能达到的发展水平的差异是教学中应该特别关注的“发展区”。教学中我们要综合考虑以下两个方面的设计：第一，考虑为学生提供什么难度的内容？第二，考虑如何铺台阶，引导学生超越最近发展区而达到下一发展阶段的水平？教学应着眼于学生的“最近发展区”，为学生提供带有难度的内容，从而调动学生的积极性，发挥其潜能，超越其“最近发展区”而达到其可能发展到的水平，在此基础上进行下一个“发展区”的发展［２］。

处理复杂的曲线运动，其主要切入点是运动的本质，基于新高考学科素养的要求，老师在教学中要引导学生从本质去思考问题，从多维角度去解决问题。将各类运动情境分类汇编给学生练习，让其见识到每一类常见的运动情境，并培养其独立分析问题、解决问题的规范性，提升数形结合的能力是其解决此类问题的关键，争取让其能够完整地分析出、规范画出全部运动过程，练习过程中避免机械性刷题。学生经过这样完整的思考过程会对知识的形成过程获得直接经验，继而培养出学生的迁移能力，让其具备以不变应万变的处理能力。

参考文献：

［１］潘学升．“一题多变、多题归一”让高三课堂更高效——以匀强磁场中“旋转圆、放缩圆”为例［Ｊ］．理科考试研究，２０２1，28（３）：３２－３４．

［２］徐美娜．“最近发展区”理论及对教育的影响与启示［Ｊ］．教育与教学研究，２０１０，24（５）：１４－１６，23．

（栏目编辑    陈  洁）