“瞬时速度”的两种教学序列探讨

摘   要：“瞬时速度”概念的学习，通常存在两种教学序列：从位置-时间函数或者位置-时间图像作为切入点进行教学。从学习心理学的角度，采取教学任务分析的方法，揭示两种教学序列各自的主要结论，分析结论获得所经过的逻辑过程，并据此给出各自的优势以及不足。从学习者易于理解的角度，选择位置-时间图像作为切入点，并以教学问题链的形式给出结合两种教学序列的一种详案。

关键词：瞬时速度；极限推理；教学任务分析

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2023）12-0068-5

人教版高中《物理》必修一“位置变化快慢的描述——速度”一节在瞬时速度概念的获得过程中，有一句话“当Δt非常非常小时，运动快慢的差异可以忽略不计，此时，我们就把叫作物体在时刻ｔ的瞬时速度”［１］。对于教材中的这句话，学生可能会产生疑问——多大的Δt才是非常非常小的？瞬时速度概念实际上是位置关于时间函数的导数，但是初升高一的学生并没有对导数进行系统的学习，作为替代需要使用极限推理的方法引导学生获得相应结论。

对于瞬时速度概念的获得，通常存在两种教学序列，一个是从位置－时间函数入手，另一个则是从位置－时间图像入手，两种序列均是合乎逻辑的，同时二者又具备着各自的优势以及不足之处。本文将从学习心理学的角度出发，通过教学任务分析的手段，分析两种教学序列各自的主要结论以及结论获得经过的逻辑过程，基于此分析两种序列的优势以及不足，并从易于学生理解的出发点给出一种结合两种序列的教学方案。

１    基于学习心理学的物理概念与规律的信息加工机制

学习心理学通过研究人类的学习机制提出，学生的学习过程是其内部对信息进行加工的过程，并遵循相应的信息加工机制，符合学生学习机制的教学才是真正有效的教学［２］。

１．１    物理概念与规律的结论获得的逻辑机制

学生在学习物理概念或规律时，总是通过实验归纳或者理论分析的途径，并经历一系列逻辑的信息加工过程获得结论。符合逻辑的信息加工方式包括穆勒五法（求同法、差异法、共变法、求同求异法和剩余法）以及演绎推理，学生通过以上的信息加工过程可以建立物理量之间的因果联系，并由此完成对物理概念与规律的学习［３］。

瞬时速度教学的主要结论分别是通过共变法、演绎推理以及极限推理的信息加工方式获得的。

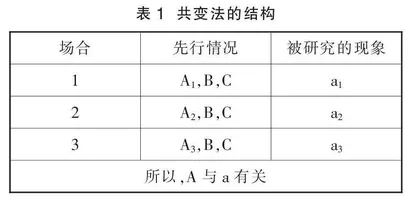
共变法的运用同样需要提供若干个场合，这些场合中只有一个先行条件发生变化，被研究的现象同样发生变化，如此便可以推断该先行条件与被研究的现象之间存在因果联系，其结构如表1所示。

演绎推理策略是通过已知的具备一般性的前提得出有关特殊性知识的结论的一种推理方式，其最基本的形式是三段论，由大前提、小前提以及结论三个命题构成，其结构如表2所示。

极限推理的运用需要已知物理量随着一个先行条件的连续单调变化而同时出现连续单调变化，假设该条件连续单调变化直至达到一个理想的极限状态，这个极限状态往往在现实中难以或者无法实现，可以推测被研究的物理量同样随之发生连续单调变化并达到对应的一种极限状态［４］。

１．２    教学任务分析

教学任务分析，可以将一个较为复杂结论的获得，分解成一系列子结论的获得，并且梳理完成获得各子结论的序列以及学习者的必备技能。其重点在于确定教学活动需要获得的结论，以及对应的一系列子结论，同时需要对子结论获得所经历的逻辑过程进行分析，并据此给出学习者参与教学活动的必备技能。根据教学任务分析，教师可以筛选出服务于结论获得的信息并进行合理有序的呈现，引导学生通过逻辑过程最终习得对应的学习结果。

２    “瞬时速度”两种教学序列的教学任务分析

２．１    瞬时速度教学需要获得的主要结论

结论：当Δt趋近于０时，的值表现为一个定值，此时的表示物体在某一时刻的瞬时速度v。

从位置－时间函数入手的子结论：

子结论ａ－１：随着Δt的减小，的值越接近一个定值。

子结论ａ－２：当Δt趋近于０时，的值表现为一个定值。

从位置－时间图像入手的子结论：

子结论ｂ－１：x-t图像上Ａ，Ｂ两点间平均速度的大小可以用割线ＡＢ的斜率表示。

子结论ｂ－２：当Ｂ点逐渐靠近Ａ点时，割线ＡＢ也逐渐向Ａ点切线靠近。

子结论ｂ－３：当Ａ，Ｂ两点重合时，割线ＡＢ也与Ａ点切线重合。

子结论ｂ－４：当Δt趋近于０时，x-t图像上Ａ，Ｂ两点间的平均速度的大小可以用过Ａ点的切线斜率表示为一个定值。

２．２    结论建立的逻辑过程

２．２．１    从位置－时间函数入手的教学序列

教师可以随意列出一个表示物体位置x与时刻t关系的运动函数，如x（t）=t2-3t+7。取由时刻t到时刻t+Δt内的一段时间，则物体对应的位移Δx可以用x（t+Δt）-x（t）得到。随意取一个时刻t=1 s，分别在Δt=１ s，０．５ s，０．１ s，０．０１ s，０．００１ s的条件下计算出位移Δx以及平均速度v=的值。

遵循共变的归纳方法，引导学生关注平均速度v=随着Δt变化的有关信息，从而得出子结论ａ－１，随着Δt的减小，的值越接近一个定值，其逻辑过程如表3所示。

遵循极限推理的逻辑方法，对子结论ａ－１进行极限处理，可以得到子结论ａ－２：当Δt趋近于０时，即t+Δt十分接近t时，平均速度v=的值等于一个定值。

当Δt趋近于０时，的值表现为一个定值，我们用表示物体在某一时刻的瞬时速度。

２．２．２    从位置－时间图像入手的教学序列

教师在位置－时间图像上随意绘制一条曲线，并在其上任意取Ａ，Ｂ两点，如图１所示。让学生找出x-t图像中蕴含的Ａ，Ｂ两点之间的时间ΔtAB以及位移ΔxAB的信息，并借此进一步找到Ａ，Ｂ两点之间的平均速度在x-t图像上的表示方式。

遵循三段论的演绎推理的逻辑过程，得出子结论ｂ－１：x-t图像上Ａ，Ｂ两点间的平均速度的大小可以用割线ＡＢ的斜率表示。

第一步，将“平均速度的表达式v=”作为大前提，经历如表4所示的三段论演绎推理过程，得到“x-t图像中Ａ，Ｂ两点间的平均速度vAB==”。

第二步，将“平面直角坐标系中直线斜率为纵坐标的变化量与横坐标的变化量的比值”作为大前提，得到“割线ＡＢ的斜率为，即”。

第三步，将“平均速度vAB的大小与割线ＡＢ的斜率大小相等”作为大前提，得到子结论ｂ－１：x-t图像上Ａ，Ｂ两点间的平均速度的大小可以用割线ＡＢ的斜率大小表示。

将Ｂ点逐渐向Ａ点靠近来缩小两点的时间间隔Δt，如图２所示，并引导学生识别割线ＡＢ随之发生的变化。遵循共变的归纳方法，获得子结论ｂ－２，其逻辑过程如表5所示。

遵循极限推理的逻辑方法，对子结论ｂ－２进行极限处理，当Ｂ点与Ａ点非常靠近，直至重合时，获得子结论ｂ－３：当Ａ，Ｂ两点重合时，割线ＡＢ也与Ａ点切线重合。

遵循三段论的演绎推理的逻辑过程，将此前获得的子结论ｂ－１和ｂ－３作为大前提，可以得出子结论ｂ－４：当Δt趋近于０时，x-t图像上Ａ，Ｂ两点间的平均速度的大小可以用过Ａ点的切线斜率的大小表示为一个定值。

我们把Δt趋近于０时的值（切线斜率）称作物体在时刻t的瞬时速度v。

２．３    两种教学序列的分析

通过教学任务分析，两种教学序列均能够通过符合逻辑的方式引导学生获得结论，但是二者在具体的结论建立过程中，对学生提出的要求有所不同。

从位置－时间函数入手的教学序列，对于学生而言不具有学习难点。学生易于通过具体的数值获得v=随Δt变化，并据此进行极限推理。当Δt不断减小，趋近于０时平均速度v=的值等于一个定值，从而习得瞬时速度的概念。其结论获得的逻辑过程中选取的函数，虽然是随意选取的，但由于子结论是针对选取的函数通过相应的逻辑过程获得的，与具体的数值存在比较强的关联，而对于其他运动状态物体的位置－时间函数是否成立未知，需要通过类似的逻辑过程进行证明，普遍性稍弱。该教学序列适合学习基础稍弱的学生。

从位置－时间图像入手的教学序列，学生首先需要将平均速度转化为x-t图像上的割线斜率，通过共变法以及极限推理得到子结论后，还需要经过将割线斜率返回到平均速度的过程。相比于从位置－时间函数入手的教学序列，学生需要额外具备与位置－时间图像相关的识图能力，同时增加了速度与割线斜率进行转化的过程，教学过程更加复杂繁琐，而且给学生带来的思维负担也更重。但是，由于位置－时间图像属于随意绘制的一条曲线，同时图像上的各点同样是随意选取的，具备相对较强的普遍性。该教学序列适合学习基础较强的学生。

３    结合两种序列的教学详案

从学生易于理解的角度来看，位置－时间图像的部分内容适合置于瞬时速度的概念学习之后，作为平均速度以及瞬时速度在图像上的表示这一部分内容供学生学习，学生在理解瞬时速度的概念之后，更加容易理解瞬时速度以x-t图像上对应点的切线斜率表示。

本文接下来将选取位置－时间函数作为出发点，在学生习得瞬时速度概念之后，通过与从位置－时间图像入手的教学序列类似的逻辑过程，引导学生习得瞬时速度在位置－时间图像中的表示方式，并以教学问题链的形式提供一种启发式教学的详案。

３．１    瞬时速度的概念（从位置－时间函数入手）

师：我们知道v=指的是物体在一段时间内的平均速度。但是在实际生活中，在一段时间内物体的速度可能发生多次变化，而不一定一直保持不变，所以只靠平均速度不能准确描述物体的运动，这就需要我们掌握物体在某一时刻的速度。同学们认为如何计算物体在某一时刻的速度呢？

生：可以采用物体在某一时刻附近的很小一段时间内的平均速度来近似表示物体在该时刻的速度。

师：我们来分析一下同学们的想法是否可行。要求平均速度需要知道哪些物理量？

生：物体运动的一段时间Δt以及这段时间内的位移Δx。

师：我们随意取一个物体的运动过程，其位置x与时间t存在关系：x（t）=t2-3t+7。取由t到t+Δt的一个时间段，这个时间段内物体的位移如何表示？

生：末位置坐标值减去初位置坐标值，即Δx=x（t+Δt）-x（t）。

师：该时间段内的平均速度怎么表示？

师：现在我们要将时间段缩短并接近时刻t，那么Δt应怎样？

生：非常小。

师：怎么做到非常小呢？随意取某一个时刻，比如在时刻t=1 s时，我们先分别取Δt=１ s，０．５ s，０．１ s，０．０１ s，０．００１ s，不断将Δt变小，观察这段时间内的平均速度的值是怎样变化的（表6）。

生：随着Δt的变小，平均速度在不断接近一个定值（子结论ａ－１）。

师：按照同学们的想法，我们让Δt不断减小，使得Δt无限小，甚至等于０，同学们认为此时的平均速度会怎么样？

生：平均速度会等于那一个定值（子结论ａ－２）。