建立虚功模型处理平衡问题

摘   要：虚功原理是理论力学中的经典理论，应用虚功原理可以简化一些物理问题的处理。通过分析虚功原理的简要发现历程，构建不同类型的物理模型，展示了虚功原理在平衡问题、圆周运动问题和电学问题中的应用。

关键词：虚功;力学;平衡;虚位移

中图分类号：G633.7 文献标识码：A    文章编号：1003-6148（2022）4-0060-3

1    虚功原理的背景

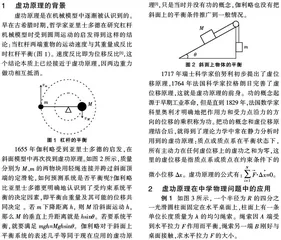
虚功原理是在机械模型中逐渐被认识到的。早在古希腊时期，哲学家亚里士多德在研究杠杆机械模型时受到圆周运动的启发得到这样的结论：当杠杆两端重物的运动速度与其重量成反比时杠杆平衡（图1）。速度反比即为位移反比[1]，这个结论本质上已经接近于虚功原理，因两边重力做功相互抵消。

1655年伽利略受到亚里士多德的启发，在斜面模型中再次找到虚功原理。如图2所示，质量分别为M、m的两物块用轻绳连接并跨过斜面顶端的定滑轮，如何预测系统是否平衡呢？伽利略比亚里士多德更明确地认识到了受约束系统平衡的决定因素，即平衡由重量及其可能的位移共同决定 。若m下降距离h， 则M沿斜面运动h，那么M的垂直上升距离就是hsinθ。若要系统平衡，就要满足mgh=Mghsinθ。伽利略对于斜面上平衡系统的表述几乎等同于现在应用的虚功原理[1]，只是当时并没有功的概念，伽利略也没有把斜面上的平衡条件推广到一般情况。

1717年瑞士科学家伯努利初步提出了虚位移原理，1764年法国科学家拉格朗日完善了虚位移原理，这就是虚功原理的前身。功的概念起源于早期工业革命， 但是直到 1829 年，法国数学家科里奥利才明确地把作用力和受力点沿力的方向的位移的乘积称为功。把功的概念和虚位移原理结合后，就得到了理论力学中常在静力分析时用到的虚功原理：质点或质点系在平衡状态下，所有主动力在任何虚位移上的虚功之和为零，这里的虚位移是指质点系或质点在约束条件下的微小位移Δx。虚功原理的公式有。

2    虚功原理在中学物理问题中的应用

例1  如图3所示，一个半径为R的四分之一光滑圆柱面固定在水平桌面上，柱面上有一条单位长度质量为λ的均匀绳索。绳索因A端受到水平拉力F作用而平衡，绳索另一端B刚好与桌面接触，求水平拉力F的大小。

虚功原理解法。假设绳索在水平拉力F作用下，A端向左移动了一小段距离Δx，则B端向上移动Δx，整体看相当于B处一段Δx长的绳索移至A处。根据虚功原理有FΔx=λΔxgR，故有F=λgR。虚功原理的应用简化了计算过程[2]。

例2 如图4所示，一均匀的柔软粗绳，单位长度质量为λ。穿过半径为R的滑轮，绳的两端吊在天花板的两颗钉子A、E上，AE之间距离为2R，滑轮轴上挂一个重物，重物与滑轮的总质量为M，不计摩擦力。求绳最低点C处的张力。

例3 如图5所示，一直角三棱柱，其斜边水平固定在地面上，三棱柱的一个底角为θ。一条质量均匀分布的软绳跨过直角两边，不计一切摩擦，三棱柱的顶端圆滑。证明当绳平衡时它两边的端点M、N必在同一水平面上。

解析：设绳总长为l，绳的单位长度质量为λ，斜面左侧绳长为s，则右侧绳长为l-s，故有左侧绳受重力为m1g=λsg，右侧绳受重力为 m2g=λ（l-s）g。设绳平衡后左边沿斜面下滑一微小位移Δx，则左侧绳重心下降高度为Δxsinθ，右侧绳重心上升高度为Δxcosθ。根据虚功原理有λsgΔxsinθ=λ（l-s）gΔxcosθ，整理得ssinθ=（l-s）cosθ，故M、N等高。

例4 如图6所示，一个内半径为R1，外半径为R2的圆柱形电容器，竖直地插进相对介电常数为εr、密度为ρ的电解液中，若将电容器接上电压为U的电源，求电解液中液面上升的高度h。

例5 如图7所示，O点为固定竖直杆上不可上下移动、只可绕杆转动的轴承，轴承通过两根长为l的轻杆分别连接质量为m的小球A、B，A、B两球分别通过长度均为l的轻杆连接质量为M、中间带有竖直孔的物块C，物块C的孔套在固定竖直杆上，A、B、C处轻杆与物体之间均用可在竖直面自由转动的铰链连接。给A、B两球一个转动力矩，使整个系统以角速度ω稳定转动后撤去力的作用，不计一切摩擦，求轻杆与固定杆之间的夹角α。

解析：以整个转动系统为参照系，A、B两球受到的惯性离心力FA=FB=mω2lsinα。设轻杆绕O点产生一个微小的角位移Δα，则A、B两球在水平方向的微小位移为Δx=lΔαcosα，竖直方向的微小位移为Δy=lΔαsinα，物块C竖直向上移动的距离为2Δy，在转动系统参照系下应用虚功原理，有FAΔx+FBΔx=mAgΔy+mBgΔy+Mg2Δy，整理可得2mω2lsinα·lΔαcosα=2mglΔαsinα+Mg2lΔαsinα，进一步整理得α=arccos。

虚功原理思想内涵容易被高中阶段学生理解，为处理较复杂的平衡问题提供了新的方法。通过几个典型的平衡问题建立虚位移模型，展示了虚功原理在解决平衡问题中的妙用。

参考文献：

[1]胡娜.力学原理的真理性反思——以虚功原理为例[J].自然辩证法研究，2016，32（5）：95-100.

[2]张朝良.例谈虚功原理在静力学问题中的效用[J].中学物理教学参考，2019，48（5）：91.

（栏目编辑    蒋小平）