核心素养导向下基于ISM和AHP的“平抛运动”结构化研究

摘   要：以ISM和AHP为研究方法，以“平抛运动”为研究对象，以物理核心素养为导向，重视物理观念、思想、方法和知识的融合，以MATLAB为运算工具，建构平抛运动的教学内容结构模型，探索核心素养导向下运用ISM和AHP法对教学内容结构化研究的可行性。

关键词：核心素养;ISM;AHP;结构化

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2022）7-0034-5

“重视以学科大概念为核心，使课程内容结构化，促进学科核心素养的落实”是《普通高中物理课程标准（2017年版）》修订的重要变化，也成为广大一线教师面临的新课题。而解决这一课题的关键就是寻找到适用于课程内容结构化的方法或路径。

ISM（Interpretive Structural Model）是美国Warfield 教授为分析复杂的社会经济系统有关问题而开发的一种解释结构模型[1]，其优点是可借助于实践经验和计算机运算形成一个层次清晰的多级进阶结构模型。将教学内容恰当分解成若干要素，运用ISM进行分析，最终也能呈现层次分明的多级进阶结构模型，为教师教学提供依据。

通过分析相关文献，我们发现在运用ISM对教学内容进行分析时存在一些问题：

（1）往往仅对知识要素进行分析，并没有考虑到知识逻辑中所蕴含的物理观念、思想和方法。这说明分析者是在对教学内容的要素划分过程中主观上将物理知识与物理观念、思想、方法进行了割裂，将知识与学科核心素养进行剥离，导致教学实施者在课堂教学中无法有效渗透和发展学生的相关核心素养。

（2）只是厘清知识之间的逻辑，并建立层级关系，但对于同一层级中各要素的权重关系都未涉及，这会造成施教者在教学过程中抓不住重点，影响教学效果。

（3）分析内容的选取往往着眼于大的模块或单元，给人一种ISM法不适于微观教学内容分析的错觉。

1    “平抛运动”结构化研究

1.1    研究路线

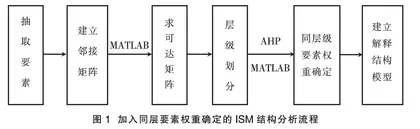
针对已有研究的不足，尝试运用ISM法对《普通高中物理课程标准（2017年版）》中“平抛运动”的相关内容进行分析，结合我们对于物理观念、思想、方法和知识的理解，在征求一线高中老师的意见后，将物理观念、思想、方法和知识均作为分析要素，运用MATLAB求解目标矩阵的可达矩阵，并对可达矩阵进行分析，建立目标层次序列，再运用AHP（层次分析法）对相同层次的要素确定其权重，进行定量分析，确保获得的教学序列的科学性，最终建立平抛运动的教学内容结构模型，研究路线如图1所示。

1.2    抽取要素

平抛运动是一种较为复杂的曲线运动，其本身就是一个运动模型，学习和理解平抛运动的过程实际上是模型建构的过程。平抛运动是解决斜抛运动的原始模型，也是后续学习各种类平抛运动的原始模型（例如研究斜面上物体的平抛和带电粒子在电场中的运动等），可以通过类比迁移平抛运动解决相关问题。因此，平抛运动模型建构所运用的思想和方法与平抛运动的知识同样重要。基于此，我们在兼顾物理知识与物理观念、思想和方法后提取出11个要素：平抛运动概念（S1），位移变化规律（S2），速度变化规律（S3），匀速直线运动（S4），自由落体运动（S5），平抛运动规律（S6），斜抛运动（S7），类平抛运动（S8），数形结合思想（S9），化曲为直思想（S10），运动的合成与分解（S11）。就各要素在学习平抛运动中起到的作用而言，其中S1～S8是知识要素，S9～S11为思想方法要素。

1.3    建立邻接矩阵

如果教师认为学生在对目标S进行学习之前必须先掌握目标S1，则称S与S1之间具有“直接关系”，并称S1为S的直接子目标。显然，此处的目标即为我们提取的要素。如果用纵轴表示高级教学目标，用横轴表示教学目标的直接子目标，若两目标之间具有直接关系则用“1”表示，若无直接关系则用“0”表示，由此建立的邻接矩阵A如表1所示。

1.4    求可达矩阵

利用MATLAB快速求解邻接矩阵A的可达矩阵M，如表2所示。

1.5     层级划分

分解各要素之间的关系：R（Si）表示可达矩阵的可达集合，A（Si）表示可达矩阵的前因集合，C（Si）表示可达集合与前因集合的交集（表3）。

根据 R（Si）=C（Si）这一条件进行层级的划分，可得S1、S2、S3为第一层级，在原有的可达矩阵上删除对应的S1、S2、S3的行和列;同理，对剩余的要素进行依次划分，可以得出S4、S5为第二层;S9、S10、S11为第三层;S6为第四层;S7、S8为第五层。

1.6    同层级要素权重确定

AHP（层次分析法） 是一种定量分析和定性分析相结合的多准则决策方法，它能够结合不同专家学者的意见，将复杂的问题分解成多个层次进行分析。运用AHP解决问题大体可以分为四个步骤：建立问题的阶层结构;构造两两比较法的判断矩阵;由判断矩阵计算被比较元素的权重;计算各层元素的组合[2]。基于上述可达集、前因集以及交集的分层结果，将模型中的各因素分层作为 AHP 的指标体系，按照Satty九级标度法（表4）构造判断矩阵，并利用MATLAB进行相应的运算。

根据可达集、前因集以及交集之间的关系运算，我们最终得到的层级有五层。其中，第一、二、三、五层同级中各含有两个及以上要素，要素间的难易程度不同，因此，我们邀请五位中学老师对同层级要素的难易程度进行标度，经两两比较法运算得出对应的判断矩阵，然后运用 MATLAB计算出判断矩阵的最大特征值λmax和特征向量，再对其进行归一化处理计算，计算出各个元素难易程度的权重系数Wi，如表5—表8所示。

计算得相应的平均一致性指标RI，如表9所示。

然后，根据层级划分以及同层级要素难易程度的权重确定结果，得到各要素的有向层级图，如图2所示。

1.7    建立解释结构模型

我们运用ISM和AHP法对平抛运动分析的最终目的是为了更好地厘清相关思想、方法、知识等各要素之间的内在逻辑关系及其在学习过程中的难易程度，为教学提供科学的逻辑指导，提高教学的有效性。只有当教的逻辑、学的逻辑和要素之间逻辑相契合一致的情况下，才会使得教学合理而有效，教学才能事半功倍。根据要素的层级划分以及同层级要素难易的权重系数，我们得出平抛运动教学内容的结构化模型，如图3所示。

在建构的结构化模型中，黑色箭头指向代表教学序列，从低级目标指向高级目标，而相同层级要素的难度也不相同，根据判断矩阵的运算得出难易程度权重系数Wi，同层级要素中权重系数Wi越大，意味着其难度越大。因此，在教学顺序中可以把Wi值小的前置，学生可以更好地接受并在其基础上学习Wi值较大的内容，学习有效性更加明显。红色箭头指向代表模型建构完成后运用平抛运动性质、规律解决问题时的逻辑次序。平抛运动的合成与分解的过程是一个双向的过程，即S4、S5合成S11与S11分解为S4、S5的过程，同时包含位移与速度的合成，v=■③，s=■④，伴随着的物理思想有S9 数形结合思想、S10 化曲为直思想等，因此结构化模型是一个紧密连接的闭环。另外，考虑到教学过程中包含众多不确定性因素，施教者也可以根据学习者的具体情况选择从哪一级开始教学，从而有针对性地开展教学，学习者可以在学习过程中对照结构化模型检验知识储备，能最快地查漏补缺完善知识结构，进而提高学习效率。

2    小结与启示

运用ISM和AHP法对“平抛运动”进行结构化分析的过程中，将知识要素和思想、方法、观念等核心素养要素一起作为提取要素，以MATLAB为运算工具，对不同层次的要素进行定量定性划分，得到关于平抛运动的结构化模型。证明运用ISM建构结构分析模型时不仅可以对大结构、大模块、大概念等较为宏观的知识要素进行逻辑分析，还可以对微观的内容进行分析，更为重要的是可以将知识逻辑中所蕴含的思想和方法作为要素进行分析。这将有助于促进核心素养教学的显性化，有利于促进教师形成核心素养导向的教学价值取向，更利于教学实施中有效促进学生核心素养的形成和发展，实现物理教育的核心价值。

参考文献：

[1]Warfield，John N.SOCIETALl SYSTEMS Planning，Policy and Complexity[J]. Journal of Cybernetics，1978，8（1）：115.

[2]唐孝玉，李文瑛，曹桂银，等.基于ISM和AHP的物流企业服务竞争力影响因素研究[J].湘南学院学报，2020，41（5）：56-62.

[3]王莲芬，许树柏.层次分析法引论[M].北京：中国人民大学出版社，1990.

[4]杨沁晓，林泽萍，严航.基于网络层次分析法的安全测试质量评价体系研究[J].网络安全技术与应用，2020（11）：29.

（栏目编辑    邓   磊）