以问题为驱动，让学习真正发生

问题是数学的心脏。教师在教学过程中，要以学生为中心，以问题为驱动，选择贴近学生“最近发展区”的问题，在生生互动、师生互动中解决问题，不断引发学生思考、探索，让学生产生兴奋感，让学习真正发生。因此，在初中数学课堂教学中，教师应设计多种问题形式，如具有层次性、开放性、批判性的问题，激发学生学习兴趣，把课堂还给学生，将学习的主动权交给学生。

一、设计层次性问题，激发学生学习兴趣

当教师提出问题时，如班级里无人回答，那么此时学生的思维可能处于一个比较混乱的状态，这就需要教师精心设计问题，让问题有层次性，环环相扣，不断激发学生学习兴趣，促进学生深入思考和探索。

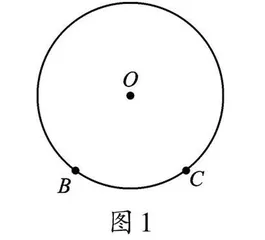
师：请在图1中画出[BC]所对的圆周角、圆心角。其中，[BC]所对的圆周角和圆心角各有多少个？

生：无数个和一个。

师：这些圆周角有什么样的关系？

生：相等。

师：为什么这些圆周角相等？（无人回答。）这些圆周角的大小和什么有关呢？

生：与圆心角有关。

师：为什么会想到圆心角？

生：因为所有的圆周角都对着[BC]，而[BC]只对着一个圆心角。

师：这些圆周角大小和唯一一个圆心角大小之间有什么关系呢？

生（齐声）：圆周角的度数等于圆心角度数的一半。

师：你能证明吗？

生：要证明无数个圆周角，好像不大可能。

师：那你能不能选择一些具有代表性的圆周角去证明呢？

生：可以。我根据圆心在圆周角的内部、边上和外部三种情况进行分类证明。（证明略。）

师：那我们最终得到什么结论？

生：同弧所对的圆周角度数相等，所对的圆周角度数是圆心角度数的一半。

【设计意图】学生很容易得出同弧所对的圆周角有无数个、圆心角就一个、这些圆周角相等的基本信息，但是怎么证明这些圆周角相等呢？很明显学生是无法直接证明或者说明这些圆周角相等的。这就需要教师设计具有层次性的问题，引导学生继续思考，发散学生思维。在证明同弧所对的圆周角的度数等于圆心角度数的一半时，教师并不需要告诉学生分类的标准，直接让学生凭着自己的直觉去分类，不断调整自己的思维，改进自己的标准。整个教学过程中，从证明同弧所对的圆周角相等到证明同弧所对圆周角的度数等于圆心角的一半，再到能不能证明，怎么去证明，这些问题关联性和层次性很强，能够很好地引导学生思考、探索，让学习真正发生。

二、设计开放性问题，激发学生的创造力

设计开放性问题往往更能激发不同层次的学生思考。学生得到的答案不相同，解题思路也不一样。学生通过在一起互动、交流，可以不断加深对问题的认识。开放性问题的设计能够鼓励学生进行深入思考和探究，从而培养他们的独立思考能力和创新能力，激发学生的创造性。

师：计算（a+b）（c+d），它的结果会少于四项吗？举例说明。

生：（a+b）（c+d）=ac+ad+bc+bd。要使结果少于四项，则这四项中必然要有能合并同类项的项。如果ac和ad能合并同类项，说明c=d，或者c=-d，然后依次类推，最后能得出结果。

师：还有其他思路吗？

生：要想结果少于四项，a、b、c、d这四个字母必然相等或者互为相反数。如果a不变，我们可以写出一些结果，a、b不变也能写出一些结果，a、b、c不变也能写出一些结果。

师：请大家把得到的结果写下来。

生（黑板展示）：（a+a）（a+a）=4a2；［（a+（-a）］（a+a）=0；（a+a）（c+d）=2ac+2ad；（a+a）（a+d）=2a2+2ad……

师：很好。其中，（a+b）（a+b）=（a+b）2=a2+2ab+b2，（a-b）（a-b）=（a-b）2=a2-2ab+b2，（a+b）（a-b）=a2-b2，这三个形式比较特殊，前两个等式叫作完全平方公式，后一个叫作平方差公式。

【设计意图】教师根据学生原有基础，设计一个开放性的问题让学生去思考，启发学生结合已学知识，发散思维，深度思考，从而更好地理解新知。这个开放性问题是为了让学生更好地理解乘法公式的来龙去脉，其实就是特殊的多项式乘多项式，让学生能主动地同化、顺构，进而对数学学习再创造，让学习真正发生。

三、设计思辨性问题，培养学生思维能力

思辨性问题是指可以引发学生反思和质疑的问题，是对之前所学知识、技能、思想、基本经验的再思考，对相关知识、结论等进一步的再审视，从而获得新的感悟。

例如，如图2，由平行四边形的性质可以得到8个基本条件，按条件类别可以得到：

边的位置关系：①AB∥CD，②AD∥BC；

边的数量关系：③AB=CD，④AD=BC；

对角：⑤∠ABC=∠ADC，⑥∠BAD=∠BCD；

对角线：⑦AO=CO，⑧BO=DO。

请你选取不同类型的两个条件，如果可以判定四边形ABCD为平行四边形，请证明；如果无法判定，请画出反例。

生：我选取的条件是①AB∥CD，⑤∠ABC=∠ADC。证明的方法有很多，主要是通过平行线的性质和判定，以及等量代换就可以证明。

师：还有其他组合吗？

生：①和③，就是我们学的定理；①和④不行，反例如图3。

生：③和⑤不行，反例如图4；⑥和⑦不行，反例如图5。

师：难道对角相等且一组对角线被另一组对角线平分都不行吗？

……

【设计意图】学生通过自己组合条件，证明问题，能够意识到判定平行四边形的方法不仅仅是我们教材上的四种方法，更是对平行四边形判定的再思考。在整个过程中，学生主动思考平行四边形的判定方法，是对原本认知的再认识，是对之前认知的完善和认知结构的重建。学生不断反思自己的思考过程，去质疑自己提出的结论，再去完善自己的思维过程，不断在旧知中收获新知。

四、教学反思

《义务教育数学课程标准（2022年版）》提出，有效的数学教学活动是教师教和学生学的统一，在教学中以人为本，让他们习得知识、应用知识和形成技能，在思考和实践中培养思维能力。数学教学问题都应该设计得让学生能不间断、尽可能地多思考。作为教师，我们设计的问题要具有层次性、开放性、思辨性。层次性问题能引发学生尽可能多的思考，问题的跨度不能太大，要做到循序渐进，所有问题之间的关联性要很强，这些问题设计目的都要指向我们所要解决的问题，但是问题之间要有一定的梯度，要让学生“跳一跳”就能够得着，享受解决问题的乐趣；开放性问题更有利于训练学生的发散性思维，一个问题可以让学生多角度、多方向、深层次地探索，可以打破传统的束缚，在课堂上生成我们需要的课堂资源；思辨性问题能让学生进行更专业的思考，通过对之前问题的再思考、之前认知的再调整，吸收别人的意见和想法，这样才能对观点、证据、假设有全面的认识，学习才有深度，有意义。