二次函数图象的“生长”教学

函数是刻画实际问题中变量之间关系的数学模型。学生要能在感性认识的基础上，研究具体的函数及性质，借助函数的知识和方法解决问题，在操作层面认识和理解函数。函数图象和性质是函数研究的主要内容。通过对函数图象和性质的研究，从数量和图形两个角度及其相互联系中，显示出函数的本质特征是数形联系和变化，这也是函数教学的主线。下面，以“二次函数的图象和性质”的第二课时内容为例试作探讨。

一、学情分析

教材是课堂教学的起点，教师需要在充分研读教材的前提下做好教学设计。从教材的安排上来看，二次函数的图象是初中阶段学生接触的最后一个函数图象，也是初中阶段非常重要的函数内容。学生在知识的储备上已经具有了对部分函数图象探究的能力，掌握了“列表、描点、连线”的图象探究基本方法。在第一课时，学生对于形如y=ax2的图象进行了研究，掌握了从对称性、顶点、变化趋势、最值等方面来探究二次函数图象的方法。本节课的学习不仅是函数知识的自然延伸，还有效地培养了学生探究函数图象的方法应用能力。

二、课例设计

课前准备：复习y=ax2（a[≠]0）的函数图象性质。

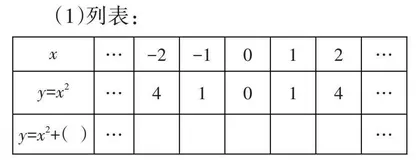
活动1 自主探究：画出二次函数y=x2+（ ）的图象。

观察表中所填数据，你发现了什么？

（2）在平面直角坐标系中描出表中各点，并把这些点连成平滑的曲线。

（3）归纳：二次函数y=ax2+k的图象性质。

【设计思路】二次函数图象的研究始于最简单的“y=x2”，在此基础上教师提问：“比前面一节课稍微复杂一点的函数表达式可以是什么样的？”自然引入到新课的教学中。这样的课堂教学设计贴近学生的最近发展区，拓展了学生对二次函数的研究空间，发展和完善了学生的认知结构。在新函数图象的研究中，以留空的形式让学生自主选择一个喜欢的常数，起到了低起点、激兴趣的作用。

在学生通过自主探究画出函数y=ax2+k的图象后，教师在课堂上给予积极的引导：“既然两种图象可以通过上下平移得到，那么在平移的过程中图象的性质哪些发生了变化，哪些没变？”引导学生结合图形变化从二次函数图象的顶点、开口方向、对称轴、增减性、最值等方面理解因“形”变而导致的性质变化，同时再从“数”的角度进行合理的代数推理。

在活动1的自主探究和性质归纳后，教师应放手让学生进入活动2的环节。

活动2 列表、描点、画出y=x2与y=（x+ ）2的图象，并观察图象之间的关系。

通过探究，归纳：二次函数y=a（x+h）2的图象性质。

活动3 函数 y=-（x-1）2+2的图象有什么性质？

【设计思路】经过活动1之后，学生自然会想到图象既然有上下平移变化，那可否进行左右平移呢？活动2的设计演变成学生对新的猜想的验证。在活动2的基础上，学生探究出二次函数图象的上下、左右平移变换，随后联想将两种平移变换联系到一起。活动3既是学生对知识的整合延伸，也可视作对活动1和活动2探究经验的结果反馈，从而依托“平移”的经验，总结出二次函数的顶点式的基本特征。

三、教学反思

当前的课堂活动设计可能过于依赖教师的视角，未能充分激发学生独立思考。改进建议包括：设计更具开放性的问题，促进学生创新思维，鼓励他们从多角度探索问题；安排小组讨论环节，让学生在小组内分享各自独特的见解，从而拓宽他们的视野；通过小组合作学习，促进学生之间的思想碰撞，使他们能够从同伴那里获得灵感。

对于学习能力较弱的学生，教师需要提供更加个性化的关注和支持。改进建议包括：设计分层次的任务，确保学生在自己的能力范围内参与并取得进步；定期进行一对一辅导，帮助这些学生克服学习障碍，增强他们的自信心；营造鼓励提问的氛围，耐心解答他们的疑惑，确保他们能够跟上教学进度；定期评估学生的学习状况，根据反馈及时调整教学策略，以满足他们的特定需求。

对于课堂知识容量，教师需要细致地规划教学内容，避免信息过载。改进建议包括：合理分配教学内容，确保学生有足够的时间吸收和理解；穿插互动环节，如小组讨论和问题解答，以促进学生的积极参与和知识内化；设计简短频繁的课堂测验，帮助学生及时巩固知识；提供课后学习资源，如在线教程和练习题，鼓励学生自主学习和复习。

在教学过程中，教师应强调从操作层面研究函数，以及从“数”和“形”的角度刻画函数性质。改进建议包括：利用实际案例引导学生理解函数性质，使抽象概念具体化，增强学生的直观感受；鼓励学生通过图形和数据来观察函数的变化，从而更深刻地把握函数的本质；在课堂上引导学生进行归纳和总结，帮助他们构建对函数性质的全面理解。

（作者单位：江苏省南京市摄山初级中学）