基于统领　构建体系　发展素养

章起始课就是开始新一章教学内容时的第一节课，具有统领全章的作用。对于起始课的这个特点，教师教学时应予以考虑，并应站在更高的层面重新审视起始课的教学，尽量在教学中发挥出起始课的特征。现行初中数学教材的章节结构安排体现了“整体→部分→整体”的模式，从编写意图上看，章头图和章头语应该是开始新一章教学时的第一节内容，顾名思义就是章起始课。章起始课应该从整体上起到统领全章的作用，因此有它的研究价值和意义。

关于章起始课的教学形式，主要有两种：（1）将章头图单独作为一节课的内容；（2）将章头图嵌入这章的第一节教学内容中。究竟选择哪种形式？需要教师结合具体的章头图和章节的特点以及学生的实际情况综合考虑，灵活选择。无论选择哪种形式，都需要教师领会教材编写者的意图，站在更高的层次上理解教材，挖掘章起始课蕴含的思想方法，发挥章起始课的引领作用。在此，笔者尝试分析章起始课的特征，以苏科版数学教材八（下）“分式”教学为例，谈谈个人的教学思考。

一、章起始课的特征

第一，从教材内容结构的编排上看，章起始课具有整体性。章建跃博士认为，数学的整体性体现在代数、几何等各部分内容之间的相互联系上，同时也体现在同一部分内容中知识的前后逻辑上。教材的编排也是从整体上进行设计的，让知识内容通过相互关系而联结形成一个系统，然后根据知识内容，将这个系统分解成若干个有序的部分，就形成各个章节。可能由于教材编排时版面容量的限制，或者由于学生认知能力的限制等原因，有的章节的内容整体感不强，没能充分展现整体性。因此，教师要在起始课教学时引领学生感受知识之间的内在联系，找到知识的生长点，“牵一发而动全身”，促使教学内容形成一个有机的整体。

第二，从思想内涵的揭示上看，章起始课具有内隐性。喻平教授认为，内隐性知识是潜藏于显性知识深层的隐性知识，是实现素养目标的基础。通常章起始课的知识比较简单，教学内容在考试中一般不会直接考查，所以容易在教学中被忽视，但这部分内容揭示了本章研究的内容框架、研究的基本思路以及研究过程中的数学思维和数学思想方法，这些也是数学学习的核心所在。因此，教师要在章起始课教学时深入挖掘内隐性知识，分析该章节的知识框架和蕴含的思想方法，促进素养目标的实现。

第三，从学习认知的过程上看，章起始课具有迁移性。教育家陶行知先生说过，数学学习是否有效，一个重要的指标是看学生的数学学习能否从一个问题迁移到另一个问题，能否从一个情境迁移到另一个情境，能否从学校课堂迁移到社会生活中。章起始课教学中整体脉络的梳理、学习框架的构建、思路方法的探究、活动经验的积累等具有迁移性，能够为学生构建“前后一致、逻辑连贯”的学习过程，让学生掌握问题研究的基本方法。因此，教师要在章起始课教学时构建一套整体思路，形成问题研究的基本路径。

二、教学实践

苏科版数学教材八（下）“分式”的教学目标为：理解分式的概念，熟练应用分式的基本性质，会对分式进行四则运算，能用分式表示现实情境中的数量关系，能列出分式方程并解决实际问题。根据教学目标，笔者安排了以下三个教学环节来引领学生对本章内容进行学习。

1.勾画基本框架，引入概念

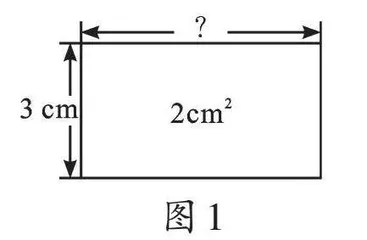
问题1：如图1、图2，已知矩形的面积是2cm2，矩形的宽如图所示，求矩形的长。如图3，若矩形的面积是bcm2呢？

问题2：填一填。

①一辆大货车3h行驶了230km，则大货车的速度为           km/h；若小汽车比大货车少用了bh，则小汽车行驶akm的速度为           km/h。

②图书馆用a元资金买书，书的单价为20元，请问图书馆可以购买           本书；若团购价每本书优惠b（b<20）元，那么按团购价可以买           本书。

问题3：上面得到的式子中，哪些是你熟悉的？你不熟悉的式子有什么共同特征？它们的区别在哪里？

问题4：你能类比分数给它们起个名称吗？

【设计意图】上述问题的设计，由特殊到一般，从包含具体数字的分数到用字母表示的代数式，体现了由分数到分式的迁移。分式的起始课教学的目的就是让学生感受到分式的由来不是凭空的，它和整式是有区别和联系的，它的产生是合理的和必要的，使得学生在后续的学习中既见树木，又见森林。

2.提供思路线索，探索性质与运算

问题5：刚才学习的分式和分数类似，想想小学里所学的分数，我们都研究了哪些内容？类比一下分式，我们可能会学习哪些内容呢？

预设：分数的基本性质，分数的加减法、乘除法，再类比分式。

问题6：取c个宽为acm、长为bcm、面积为2cm2的矩形，将它们拼成下图（图4）所示的大矩形，你能用不同的方式表示a吗？

预设： a=[2b]=[42b]=…=[2cbc]。

总结：分式也具有和分数类似的基本性质。

问题7：根据如下拼图（图5），你能表示b+c吗？

预设：b+c=[2a]+[1a]=[3a]。如果将两个长方形叠合，同样可以计算b-c。

【设计意图】通过探索活动，促进思想方法正迁移。先组织学生回忆分数的性质和运算，由数的运算过渡到式的运算，让学生经历问题产生的原因、问题探究的过程、研究结果的应用，掌握研究这类问题的方法，获得研究问题的经验，自觉运用该思路，形成研究问题的基本策略，并一以贯之加以训练，再迁移到对其他问题的研究之中，促进迁移能力的提升。

3.挖掘隐性资源，探究分式方程

问题8：京沪铁路是我国东部沿海地区纵贯南北的交通大动脉，全长1462km，是我国最繁忙的铁路干线之一。如果货车的速度为akm/h，客车的速度是货车的2倍，那么：

①货车从北京到上海需要多少时间？

②客车从北京到上海需要多少时间？

③已知从北京到上海的客车比货车少用6h，你能用方程描述其中的数量关系吗？

问题9：列出的式子[1462a]、[14622a]是分式吗？

问题10：[1462a]-[14622a]=6是整式方程吗？你能给它起个名称吗？

【设计意图】算式只能用已知数进行运算，方程建立了已知数和未知数之间的联系。在复杂的问题中，学生通过已知量很难计算出结果，而利用方程可以找到已知量和未知量之间的关系，求得未知数的值，从而解决问题。教师教学时要挖掘这些隐性资源的价值，让学生感受从算式到方程的必要性，并能感受整式方程与分式方程的区别，进而让章起始课教学发挥从数学现象认识到数学概念建构的过渡作用，让章起始课教学中的内隐性数学思想走向外显性的迁移运用，发挥数学的育人价值。

三、教学思考

良好的开端等于成功的一半。数学的章起始课教学，事关整个数学章节单元教学的效率和成败。章起始课教学，尤其要重视方法，讲究技巧，如果备课不巧，教学不好，讲解不透，则意味着没有把学生领进这个章节单元知识的大门，意味着可能会带给学生数学学习的挫败感。今后再花更多时间“炒冷饭”，即使能化解这个“知识疙瘩”，也已经很难化解学生累积下的“数学恐惧”了。

1. 激发学生兴趣和探索欲

激发学生对本章内容的学习兴趣和探索欲望，是章起始课教学的第一目标。章起始课教学，是这一章节单元教学的热身，不能急于求成。已学知识的调取和铺垫、数学日常情境的引入和创设是章起始课教学必不可少的。在本节课中，笔者创设了一个学生熟悉的，感兴趣的，低起点、高立意的问题情境，让学生初步感知本章知识的价值和意义，通过这节课的学习，引导学生搭建起沟通章节知识的桥梁。

2. 循序渐进地教学

由浅入深、由现象到规律、由已知到未知的循序渐进是章起始课教学的第一方法。章起始课教学，要通过鲜活的数学材料，引发学生质疑猜想，唤醒学生强烈的问题意识，启发学生的数学思维。本节课，笔者让学生从实例中列出代数式，然后经过分析，类比分数，归纳出分式概念。学生从中不仅积累了数学活动经验，而且通过类比分数的研究方法，构建了研究分式的框架，获得了对本章内容的整体认识，能将所获得的经验自然地迁移到分式的其他内容的学习中，体会研究代数问题的一般思路，在掌握数学方法的同时，提高自主学习的能力。

3. 整体感悟，关注本质

整体感悟、关注本质是章起始课教学的第一要务。章起始课不适合对知识的具体细节做过多的“完美”阐释，应重点向学生展示本章内容框架，让学生感受本章的概念产生和发展的基本过程，以及在此过程中形成的数学文化，激发学生学习本章内容的数学使命感，使学生体会研究本章问题的数学基本思想。对于本节课，要突出的是类比和转化的教学思想。由于分数与分式具有形式相同、数式相通的特点，笔者在本节课的教学中设计了不同类型、不同层次的问题，通过开放式、交流式、追问式、总结式、反思式等多种方式引导学生进行对话交流、思维碰撞，逐层深入问题的本质。学生主动利用已有知识经验寻找解决问题的突破口，经历从具体到抽象、从特殊到一般的认识过程，体会研究代数问题的一般思路。这些思想方法润物无声地渗透，对学生认知结构的构建、优秀思维品质的形成都将起到积极的推动作用，能很好地培养学生的数学核心素养。

（作者单位：江苏省张家港市后塍学校）