高中物理拔尖人才培养研究

[摘 要]高中是培养物理拔尖人才的重要时期，是学生思想品德、关键能力形成的重要阶段。南宁市第三中学作为广西基础教育的窗口学校，作为广西奥赛第一校，在培养物理拔尖人才方面积累了一定的经验。文章基于南宁市第三中学的办学理念和育人模式，借助新教材、新课程、新高考综合改革的东风，探索南宁市第三中学独具特色的高中物理拔尖人才培养模式。

[关键词]高中物理;拔尖人才;五育并举;大单元设计;创新思维

[中图分类号]    G633.7            [文献标识码]    A          [文章编号]    1674-6058（2022）18-0001-04

近年来，我国在航空航天、5G、人工智能等重大领域取得了举世瞩目的成就，但是在高端芯片等一些高精尖的技术领域，还有许多不足，还存在被人“卡脖子”的现象。要想在“卡脖子”技术领域有较大的突破，就需要各方努力，需要有更多基础学科拔尖人才的加盟。2020年教育部出台的《关于在部分高校开展基础学科招生改革试点工作的意见》（也称“强基计划”）显得意义非凡，“强基计划”的提出，让人们的目光投向对国家战略有帮助的基础学科。高中是物理拔尖人才成长的重要阶段和关键时期，因此，要特别重视高中物理拔尖人才的培养。

随着新课程、新教材的全面实施，要推进适应学生全面而有个性发展的教育教学改革，推进有创造性改变的课堂教学改革。本文结合南宁市第三中学的教学实践，从以下三个方面进行分析探讨。

一、基于拔尖人才全面发展的五育并举

（一）完善德育为先的实践型德育模式

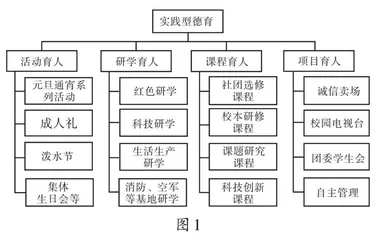
立德树人应立德在先，育人先要育德。南宁市第三中学建于1897年，已有120多年的办学历史，在长期的探索实践中，确立了“敦品力学”的校训，形成了“真·爱”教育的办学思想，构建了实践型德育模式（如图1）。让学生从实践中得到体验，收获做人做事的感悟，从而培养学生的高尚品格、家国情怀、国际视野及担当精神。

（二）基于选课走班的智育发展模式

南宁市第三中学新高一启动了新课程、新教材的改革，采用“3+1+2”的考试模式。学校本着以人为本、差异化竞争的理念，尊重学生的意愿和选择，12个组合，学生一共选择了11个组合，形成了20个行政班，41个教学班，其中物理拔尖人才，选择了物理化学生物、物理化学地理、物理化学政治三个组合。南宁市第三中学以课程为主要抓手，探究课程育人策略，着力打造通识类课程、研讨类课程、特长类课程、探究类课程、体验类课程五类选修课程，并展开国家课程的最优实施及课堂教学重构（如图2）。让物理拔尖人才有选择权、有获得感、有成就感，让智育回归自然，还教育以浪漫。

（三）基于个性化需求的体育项目式课程

体育与健康是高中课程中基于生命、指向生命、提升生命质量的学科。南宁市第三中学基于学生的兴趣爱好及体育特长进行分类分层指导，创设了丰富多样的“基础与特色相辉映、兴趣与特长相促进”的新型体育项目式课程，并把选择权交给学生，满足学生多种不同的锻炼需求，这有利于物理拔尖人才的个性化发展以及人际交往与合作精神的培养，有利于促进物理拔尖人才身心健康，有利于提高物理拔尖人才的生命质量。

（四）基于艺术熏陶的美育课程和活动

南宁市第三中学各年级的美育课程开展完善齐全，高中模块课程开展丰富多彩，音乐与歌唱，音乐与舞蹈，音乐与戏剧，音乐与演奏，均有课程体现。美育课程以校本特色课程、校园风景速写、书签设计、拼贴画制作、艺术设计、影视与摄影等方式进行呈现。学校艺术类实践活动丰富多彩，如高一红歌赛、高三音乐会、高二高雅音乐进校园、学校新蕾文化艺术节、主持人大赛、元旦通宵晚会、音乐节、舞社专场、影像节等均为学生提供了展示艺术才华与实践的机会。这些美育课程和活动能有效培养物理拔尖人才的艺术鉴赏能力、审美能力、丰富的想象力。

（五）多举措开展劳动教育

劳动教育与德、智、体、美的发展密不可分，在“五育”中起着奠基的作用。响应国家物理拔尖人才培养战略，南宁市第三中学开展了劳动价值观研讨会，组织学生参与学校的植树活动，组织学生开展“鱼菜共生”大棚种养活动，让学生参加校园内每周一次的网格化劳动等。通过各种形式的劳动，有效培养了学生的劳动技能，进而培养学生爱校、爱家、爱城市、爱国家的情怀。

二、基于物理拔尖人才培养的课堂教学改革

培养物理拔尖人才，不可能仅靠传统的教学方式，要有针对拔尖人才培养的课堂教学模式。具体可以基于大单元设计课堂教学模式，引导学生深度学习，让高中物理教学与大学物理教学有效衔接，并适时开展能引导学生深入思考的项目式学习。

（一）基于大单元设计课堂教学模式

基于大单元设计的课堂教学模式，打破了传统的一节一教案的零碎式教学模式，建立了以素养为导向、以单元主题为主线、以学习目标为焦点、以学习评价来激励的大单元整体教学模式。“大单元设计”的理念让教师和学生不局限于小打小闹，能够从全局和大视野去观察、认识和理解同一大单元的大概念、大观念，让物理拔尖人才感受到这种不同章节的关联与和谐统一，培养物理拔尖人才的大局观。下面以“功和能”为例阐述大单元设计的路径（如图3）。

（二）深挖教材，做好高中物理与大学物理的衔接

比如在讲“单摆”的规律时，单摆周期公式在高考要求是定性了解，在培养物理拔尖人才时，可以在高中物理教材的基础上加深和挖掘，类似的还有弹簧振子，可用导数进行推导。

对弹簧振子（如图4）有：

由实验已经得到位移[x=Asin（ω t+φ）]，

求导得速度[v=Aωcos（ω t+φ）]，

再求导得到加速度[a=-Aω2sin（ω t+φ）]，

根据牛顿第二定律求加速度有[a=-kxm]，

故a=-[kAsin（ω t+φ）m]，

又[ω]=[2πT]，则[T]=[2π][km]。

对单摆（如图5）有：

在单摆中回复力F=-mgsin[θ]，

当[θ] < 10°时，F=-mg[xl]=-kx，即k= [mgl]，因为单摆和弹簧振子的回复力遵循一样的规律，代入弹簧振子的周期公式得：

[T=2πlg]

对高中物理教材的深度挖掘可以让学生对概念的理解更深刻，而与大学物理教材的衔接，可让学生站得更高，使学生的高阶思维得以锻炼，核心素养得以培养。

（三）开展项目式学习，引导学生深入思考

培养物理拔尖人才，需要开展学生感兴趣的项目式学习，以引导学生深入思考，从而培养学生的发散性思维和抽象思维。比如，以小组为单位开展高考题研究，并形成报告。下面是某小组对2021年高考全国甲卷物理压轴题（第25题）的研究。

该题计算量大且灵活，能很好地体现高考对物理学科核心素养的考查，对学生的综合能力要求非常高[在此仅以该卷第25题的第（2）（3）问为例，让学生分小组从不同的视角进行探析]。

[原题]如图5，长度均为[l]的两块挡板竖直相对放置，间距也为[l]，两挡板上边缘[P]和[M]处于同一水平线上，在该水平线的上方区域有方向竖直向下的匀强电场，电场强度大小为[E];两挡板间有垂直纸面向外、磁感应强度大小可调节的匀强磁场。一质量为[m]，电荷量为[q（q>0）]的粒子自电场中某处以大小为[v0]的速度水平向右发射，恰好从[P]点处射入磁场，从两挡板下边缘[Q]和[N]之间射出磁场，运动过程中粒子未与挡板碰撞。

已知粒子射入磁场时的速度方向与[PQ]的夹角为[60°]，不计重力，求：

（1）求粒子发射位置到[P]点的距离;

（2）求磁感应强度大小的取值范围;

（3）若粒子正好从[QN]的中点射出磁场，求粒子在磁场中的轨迹与挡板MN的最近距离。

【试题解析】本题第（1）问考查带电粒子在静电场中的类平抛运动，解法从略。本文重点从不同角度探析第（2）问和第（3）问的三种解法。

解法一：常规解法

第（2）问：如图7，对粒子，从[Q]射出，相应的圆周运动半径为[r1]，磁感应强度为[B1]，设[P]点速度[v]与[PQ]边的夹角为[α]，[α=60°]。

由速度关联有：[v=v0sin α]，

由几何关系得[r1=l2sin α]，

由牛顿第二定律有：[qvB1=mv2r1]，

联立方程解得：[B1=2mv0ql]。

如图8，从[N]射出，[C]为[PN]中点，相应的圆周运动半径为[r2]，磁感应强度为[B2]。

由几何关系有：[PC=PN2=2l2]，[r2=PCcos 75°]，

由牛顿第二定律有：[qvB2=mv2r2]，

联立方程解得：[B2=1-33mv0ql]，

又因为粒子未与挡板碰撞，故[B2<B<B1]，

综合以上分析可得：[1-33mv0ql<B<2mv0ql]。

第（3）问：如图9，对粒子，从[F]射出，相应的圆周运动半径为[r3]，[PF]与[PQ]的夹角为[β]，[PF]与速度[v]间的夹角为[γ]。由几何关系知：

[tan β=12<33]，故[β<30°]，

又由[β+γ=60°]，可知速度方向在磁场中偏转的角度为：[2γ=2（60°-β）>60°]

速度偏转角度大于60°，因此点[F]上方存在速度方向竖直向下的点[G]，点[G]距离[MN]最近且为[dmin=GH]，[△][PQF]中有：[sin β=55]，[cos β=255]，

故[sin γ=sin（60°-β）=155-510]，

[又 r3=PF2sin γ=PDsin γ，PD=PF2=l2+l222=5l4 ]。

由几何关系有：[dmin=l-r3-r3sin 30°]。

可得[dmin=39-10344l]。

【小组评析】采用常规解法充分考查了学生利用数学知识解决物理问题的能力，需要能将较复杂的实际问题中的对象和过程转换成物理模型，对综合性物理问题进行分析和推理，获得正确结论并做出解释。

对本题来说，第（2）问求[r2]的方法还有很多，比如用余弦定理或正弦定理等，第（3）问也可以用轨迹圆的方程求解，这些做法对数学计算能力有较高的要求，都可以归为常规做法。那么，能否换个角度重新审视这个问题呢？答案是肯定的！

解法二：利用动量定理求解

第（2）问：建立如图10所示的坐标系，由[x]方向动量定理有：

[qvyBΔt=-mΔvx]，

[qBΔy=-mΔvx]，

两边求和可得：

[qB（y2-y1）=-m（vx2-vx1）]，

对粒子，由[P]运动到[Q]，有：[qB1l=2mvx=2mvsin 60°]，

得：[B1=2mv0ql]。

建立如图11所示和坐标系，由几何关系有[PN=lcos 45°=2l]，

对粒子，由[P]运动到[N]，有：[qB22l=2mvx=2mvsin（60°-45°）]，