新工科背景下“复变函数与积分变换”教学改革探索

［摘 要］ 新工科背景下对人才培养提出了新的要求，其内涵是以立德树人为引领，培养多元化、创新型工程人才。新工科教育理念突出了数学理论和方法对工科专业的支撑作用。在新工科的教育理念和背景下，针对当前“复变函数与积分变换”教学中存在的不足，从课程思政、教学内容、教学方法、教学模式、考核模式等方面进行了改革，以提高学生的学习兴趣、提高教学效果，培养符合新工科要求的具有高级思维能力、实际应用能力及正确价值观的创新型人才。

［关键词］ 新工科；教学改革；课程思政；可视化教学

［基金项目］ 2022年度山东省精品示范课“数学物理方程”（16202210003）

［作者简介］ 牟海宁（1979—），女，山东栖霞人，理学博士，中国石油大学（华东）理学院讲师，主要从事数值计算和偏微分方程研究。

［中图分类号］ G642.0 ［文献标识码］ A ［文章编号］ 1674-9324（2024）26-0045-04 ［收稿日期］ 2023-09-28

引言

在新工科背景下，各高校需秉承立德树人根本任务，以培养应用型、创新型人才为目标，积极开展教育教学改革［1-2］。“复变函数与积分变换”是高等院校中许多工科专业的重要数学基础课。复变函数论在流体力学、电磁学等领域有着广泛应用，而积分变换理论在信号处理、自动控制、图形图像处理、地质勘探等工程技术领域有着重要应用［3］。学习此课程能够培养学生的数学素养和应用能力，培养学生分析问题、解决问题的能力。“复变函数与积分变换”内容主要包括：复数与复变函数、解析函数、复变函数积分、级数、留数及其应用、共形映射、傅里叶积分变换和拉普拉斯变换等，内容比较抽象、理论性和实用性强，很多学生认为课程比较难学，有畏难心理。为提高学生的学习兴趣，提升教学效果，培养学生的创新思维能力，我们从课程思政、教学内容、教学方法、教学模式以及考核模式等方面进行了教学改革探索。

一、课程教学中存在的问题

根据十多年的教学经验以及调查研究发现，“复变函数与积分变换”教学中存在以下问题［4］。

1.课程思政教育不足。教师对思政的认识和重视不足。多数教师只注重传授专业知识而忽视了思政教育。“复变函数与积分变换”课程中蕴含着丰富的思政元素，但教学过程中缺少思政教育，未能充分发挥其育人功能。

2.教学内容与专业结合不够紧密，缺乏前沿性知识。在传统教学中，面对不同专业、不同层次的学生，教学内容是统一的，学生只能被动接受教学内容和进度，导致学生对课程的学习兴趣打折扣。

3.教学模式单一。以教师为主体的灌输式教学方式无法较好地激发学生的学习主动性和积极性，不能有效地追踪到学生的学习效果。如何让学生成为学习的主体，激发其学习兴趣和主动性是急需解决的关键问题。

4.教学手段和教学方法单一。由于复变函数理论的抽象性特点，如何将传统的板书教学与PPT教学两者有机结合起来是关键，引入可视化教学，将抽象问题直观化。

5.考核模式单一。传统的考核方式是平时作业+期末考试，缺少对学生的过程化考核，无法对学生的学习情况进行持续追踪和监督，缺乏教育评价的诊断和改进功能，导致部分学生学习效果欠佳。

二、教学改革措施

新工科的教育背景下，要求在教学中以“学生为中心”，以专业需求为导向，培养具有高级思维能力、创新能力的德才兼备的可持续性发展的人才。针对上述提出的问题及新工科的教育理念，采取以下几个改革措施。

（一）加强思政建设

充分挖掘“复变函数与积分变换”课程中的思政元素，将其融入教学过程中，激发学生的学习热情，提高学生的探索精神，培养学生的科学素养。例如，第一堂课介绍复变函数的发展历史及其在实际工程领域中的应用时，向学生介绍柯西、黎曼和魏尔斯特拉斯等科学家对复变函数领域做出的贡献，使学生认识到复变函数论发展至今是一代代科学家艰苦努力取得的成果，以此激励学生不畏艰苦、勇于追求科学真理。

“复变函数与积分变换”是“高等数学”的后续课程，许多定理和结论都是“高等数学”在实数域中的推广和发展，但许多结论和实函数的结论不同，甚至相悖。如在复数域中，负数可以开平方根并且任何一个非零负数开n次方根有且仅有n个不同的根等；在复变函数中，指数函数ez是周期函数，三角函数sin z和cos z为无界函数。因此，在教学中引入类比教学法，引导学生找到相关结论的异同，引导学生用发展的思维思考问题，培养学生的探究精神和严谨的科学精神。

柯西积分公式和高阶导数公式说明对于解析函数来说，区域内部的函数值完全可由边界上的积分值来确定，即“边界决定内部”的数学思想，这彰显了解析函数局部反映整体的性质，由此可引导学生在学习时要善于发现、总结数学规律，探究数学思想，有助于培养良好的数学思维。

在讲解洛朗级数时，向学生介绍科学家洛朗理论结合实际的能力非常强，让学生学习洛朗理论应用于实际的能力。同时，教师要搜集、提炼复变函数与积分变换知识在实际工程中的应用实例，建立相关案例库，教学时有意识地培养学生的理论联系实际的能力和理论应用于实际的能力。

总之，我们应将思政教育贯穿教学始终，对学生进行价值引领，但要注意思政教育应与课程内容有效融合，不能生搬硬套。

（二）教学内容改革

1.教学内容与专业紧密结合。搜集并建立专业案例库，在教学内容上选择与学生专业相结合的案例，提高学生的学习兴趣。例如，讲解解析函数在实际中的应用时，对力学专业的学生，引入解析函数在平面流体场中的应用案例；对物理专业的学生，引入解析函数在平面静电场中的应用案例。讲解拉普拉斯积分变换时，对电信专业的学生引入信号处理方面的应用实例；讲解傅里叶积分变换时，对光电专业的学生引入光学方面的应用实例等。

2.教学内容与前沿知识相结合。在本课程教学中，存在学生的基础知识水平有较大差异的情况。部分学生由于“高等数学”基础较弱，学起来吃力，而基础好的学生知识接受能力强，渴望新知识。因此，在注重基础知识和基本技能的前提下，要适当引入高阶性、前沿性的知识。这要求教师要及时增加知识储备，及时了解复变函数领域和积分变换领域的前沿进展。在教学过程中适当引入前沿知识，提高教学内容的前沿性和高阶性，满足不同层次学生的学习需求，真正做到以尊重学生个性化发展为前提的分层次教学。此外，可在每一章引入相关的拓展知识问题，组织学生进行分组研讨并汇报，培养学生的创新思维和解决问题的能力以及团队合作能力。

（三）教学模式改革

在教学过程中始终遵循以“学生为中心”的教育理念，让学生成为学习的主体，采取线上线下混合教学模式［5］，充分发挥学生的学习积极性。

线上线下混合教学模式是学生线上自学和传统线下教学相结合的新型教学模式，充分利用信息技术和网络资源，借助于慕课、爱课程、智慧树等平台进行辅助教学。目前所采取的线上线下混合教学模式是以“线下为主，线上为辅”。对于线上自学课，教师将学习任务在平台上提前布置给学生，学生学习线上教学视频、教学课件等，并在规定时间内完成相关测试。为此，教师需要根据课程内容，制订好课程计划。

1.对教学内容和教学课时进行划分。根据内容难易程度及与前后的关联程度，将课程内容分为学生线上自学内容和线下讲授内容两部分。一般线上课时占总课时的20%左右。

2.制定自学导学单。以学习目标、问题引入、学习内容、学习要求、作业、思考拓展、思政元素为模块做成导学单，引导学生进行自学。在智慧树等平台向学生布置学习任务，让学生按照导学单的要求进行自学，并完成相关作业和测试。

3.布置测试。每次自学都紧跟一次线上测试以检验学生的学习效果。课程组教师提前做好题库，按知识点将试题分类，借助于智慧树平台将测试布置给学生。试题与学习内容紧密关联，按难易程度分类，每次测试都随机组卷，打乱题目顺序，并让学生在限定时间内完成。

线上自学过程中，学生可以随时通过QQ、微信等及时与教师交流，教师要及时为学生答疑解惑。自学后紧跟的线上测试可以反馈学生的学习情况。这样线下授课时，教师可以有针对性地进行教学，提高教学效果，线下教学时可利用信息技术与学生进行有效互动。例如，课中充分利用雨课堂，讲课过程中针对重要知识点及时插入雨课堂测试，随时掌握学生学习情况。对大部分学生掌握欠佳的知识点进行再次讲解，以保证教学效果。这样既可以调动学生的学习积极性，又实现了对学生的过程化考核。

自学视频可以选取慕课、爱课程等网站的精品课程视频，课程组教师也可录制微课视频。将教学内容系统分类后进行“碎片化”处理，录制时长较短的微课视频，学生可以随时随地学习。在每个视频中都加入弹题，学生在学习完某部分知识后，通过做弹题理解、检测学习重点和学习效果。对于难度较大、比较抽象的问题，还可录制答疑视频，有需要的学生可以观看解惑。通过录制拓展视频，满足学生的学习成长需求。线上线下混合式教学模式可以充分调动学生的学习积极性和主动性，培养学生的自学能力和科学探索能力。

（四）教学手段和教学方法改革

1.板书与PPT相结合。在线下教学时，应将板书教学和PPT教学有机结合，既可以节省时间、丰富教学内容、增加课堂的信息量，又可以保证课堂教学有效性。例如，涉及定理证明时，应结合启发式教学方法，进行板书讲解，便于学生思路跟进，有助于培养学生的逻辑思维能力；讲述函数的性质时，借助于PPT演示，有助于学生的直观理解。

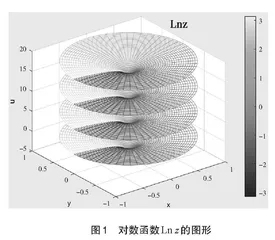
2.可视化教学。由于“复变函数与积分变换”课程的理论性强、内容比较抽象，很多学生感到乏味、难以理解。在教学过程中引入可视化教学手段，可将抽象的问题直观化，有助于学生对内容和内在规律进行分析与理解。例如，在讲解对数函数时借助于其可视化图形，可看出其多值性，以及各个值的实部、虚部之间的关系。如图1所示，画出的是Ln z=ln |z|+iarg z+2kπi在k=0，1，2，3时的图形。从图1可以看出，对数函数Ln z的四个值的实部值（竖轴代表函数的实部值）相等，而虚部值（颜色代表函数的虚部值）之间相差一个常数。再例如，讲解傅里叶积分变换时，利用可视化图形有助于理解象函数的物理意义。如图2所示，绘制的是矩形脉冲函数的傅氏变换的频谱图。由图2可理解象函数的模代表了各个频率成分的函数在信号中所占的比重。

可视化教学可以使教学过程生动化、形象化、直观化，有助于学生理解抽象知识，能够提高学生的学习兴趣。

（五）考核方式改革

基于新工科内涵，需建立能够全面评价学生的综合能力的多元化考核模式。由于本课程实行线上线下混合式教学，增强了过程化考核，使得考核评价更有时效性和全面性。本课程的考核采用多维度的评价方式，评价分为以下几个模块。

1.课程小论文。让学生撰写基于本课程且与专业相关的课程论文，并组织答辩。论文评分要素有：（1）选题情况（与本课程的相关度、难易程度）；（2）问题解决情况（模型建立、求解方法、求解步骤、程序实现）；（3）总结（结果分析与探讨）；（4）论文书写情况（逻辑性、规范性、充实性）；（5）答辩情况（PPT讲解、语言表达、回答问题）。从深度和广度上对学生进行评价，有助于培养学生的创新能力。

2.过程化考核。包括平时作业、课堂表现，以及每次自学测试等，过程化考核贯穿整个学习过程，有助于对学生的学习情况进行诊断和改进。

3.期末考试。期末考试试题将基础理论知识测试和实际能力测试并重，以培养学生解决实际问题的能力。

结语

笔者将上述改革措施应用于2020级和2021级石油工程专业、电子通信专业、地学专业，进行了两个学期的“复变函数与积分变换”课程教学试验，发现与之前相比，学生的学习积极性有了很大提高，也取得了较好的教学效果。经过调查，学生对教学的满意度也有所提高。新工科建设对教师的教学提出了新的要求，我们必须不断深化改革教学内容和教学方式，提高教学质量。