“概率统计”课程思政教学研究与实践

［摘 要］ 围绕激发学生学习兴趣和潜能深化，对“概率统计”课程思政教学进行深入研究与认真实践。设计贯穿教育教学全过程的课程思政教学体系，将思政元素以隐性的方式融入“概率统计”课程的教学目标、教学大纲、课程标准、教学设计等各个方面，具体落实到教学内容、教学方法、教学评价等教学活动的各个环节中。深度挖掘相互融合匹配的教学内容与思政元素，采用灵活多样的教学方法，在进行知识传授、能力培养的同时，强化对学生的价值引领，培养学生的科学精神和家国情怀，确保课程思政建设落地落实。

［关键词］ 概率统计；课程思政；思政元素

［中图分类号］ G642.0 ［文献标识码］ A ［文章编号］ 1674-9324（2024）31-0173-04 ［收稿日期］ 2023-05-19

课程思政的本质是立德树人。最早于2014年由上海市教育委员会提出课程思政的概念并在上海的一些高校进行推广，成效良好。2020年5月，教育部印发的《高等学校课程思政建设指导纲要》明确指出，全面推进课程思政建设是落实立德树人根本任务的战略举措。［1］2016年12月，习近平总书记在全国高校思想政治工作会议中明确提出：要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，实现全程育人、全方位育人，努力开创我国高等教育事业发展新局面。［2］2022年7月，教育部等十部门关于印发《全面推进“大思政课”建设的工作方案》提出建设全国高校思政课教研系统［3］。因此，近年来，将思政元素融入各类专业课堂的教学研究成为关注热点。“概率统计”是高校理工经管等专业的公共基础必修课。该课程在人才培养的整个课程体系中起着承前启后的重要桥梁作用，其思想和方法为学生的后期发展起到不可或缺的支撑作用，因此在教学中加强课程思政建设对学生的全面发展将产生深远影响。关于“概率统计”的课程思政教学改革与实践已从教学内容、实践路径、教学方法等方面取得不少成效［4-6］。

一、课程思政教学体系设计

构建“概率统计”课程思政教学体系，围绕价值塑造、能力培养、知识传授“三位一体”的教学目标，开展教学研究，建设教学资源，改革教学方法。“概率统计”教学的知识目标为使学生掌握处理随机现象的基本思想、基本理论和基本方法；能力目标为能用概率观点和统计思想去思考和处理实际问题，提高学生基于不确定性的科学思维能力和实践创新能力；素质目标为在潜移默化中坚定学生理想信念、厚植爱国主义情怀、加强品德修养、增长知识见识、培养科学精神，提升学生综合素质。为了将价值塑造润物无声地融入知识传授和能力培养中，就需要合理地设计教学方案，将课程思政贯穿于全部日常教学活动，寓道于教、寓德于教、寓教于乐，培养学生求真、求是、求善、求美的态度和精神，落实立德树人根本任务。

将思政元素以隐性的方式融入“概率统计”课程的教学目标、教学大纲、课程标准、教学设计等各个方面，具体落实到教学内容、教学方法、教学评价等教学活动的各个环节中。比如，在设计教学大纲时，将价值塑造与知识传授、能力培养有机地融合在一起，将思政教育融入教学大纲的每个环节，确保正确的价值观、科学的哲学思想渗透到整个课堂教学中［7］；在进行教学设计时，深度挖掘思政元素，如盐入水般融入教学内容，采用灵活多样的教学方法，潜移默化地将思想政治教育渗透到专业知识传授中，实现知识目标与价值塑造相统一。具体来说，可以在概念的形成过程中介绍其起源、发展和应用，在问题的求解过程中帮助学生实现认知和技能的深化和固化，在结论的推导过程中培养学生思维的严谨性、灵活性、批判性和独创性，在规律的被揭示过程中进行辩证唯物主义思想教育；将知识点精心创设为激发学生兴趣的实际案例，如“三门问题”、保险问题、抽签问题、敏感问题调查、种群灭绝问题等，在利用“概率统计”知识揭示其内隐本质的同时，激发学生的思想共鸣，引导学生主动发现知识背后的价值趋向，树立正确的世界观、人生观和价值观；同时，可以充分发挥集成了爱课程（中国大学MOOC）、学银在线（学习通）、学堂在线（雨课堂）等众多课程平台的国家高等教育智慧教育平台的优势，对学生进行思想品德教育，通过交流学习心得、小组讨论、同伴互评等形式引导学生积极思维，实现学生自主学习和合作学习，增强学生的“参与感”与“融入感”，培养学生创造性思维、高水平推理和批判性思维等能力。

二、课程思政元素

“概率统计”课程思政元素是指在“概率统计”教学中注入思政的内容和元素。课程思政是浸润价值塑造的教学方法。围绕“三位一体”的教学目标，教学团队对“概率统计”的课程思政实施要领和具体方法进行了探索和思考，运用人文思想去诠释“概率统计”中的一些概念、原理、公式与现象，展示事理之间的相通性，体现人类探索知识的轨迹、凝练知识的智慧、应用知识的历程，培养学生的人文情怀；注重课程思政元素融入教学过程，激发学生的家国情怀，锻炼学生辩证思维和勇于探索的创新精神等；通过充分挖掘“概率统计”课程蕴含的课程思政元素，促进思政教育与课程教学的相互融合，提升学生思想政治素质，确保课程思政建设落地落实、见功见效。

同一教学内容可以挖掘出不同的思政元素，且同一思政元素也可以蕴含在不同的教学内容中，教学内容与思政元素相互融合，实现思想政治教育的潜移默化。比如，在绪论章节，通过介绍我国数学家在“概率统计”方面的研究成果和贡献，增强学生的民族自豪感与荣誉感，激发学生的爱国热情。频率与概率的关系体现出唯物主义偶然性与必然性的对立统一。贝叶斯公式的基本思想是大胆假设、小心求证、不断调整、快速迭代，不认死理，根据新的信息，不断更新个人认知，永葆灵活性思维。在贝叶斯公式章节，还可以通过对寓言故事“狼来了”的定量分析，说明诚信是立命之本。孔子曰：“人而无信，不知其可也”。可从伯努利试验的角度分析“水滴石穿”，有志者事竟成，体现了唯物主义偶然性与必然性的辩证关系，由量变产生质变；也可通过伯努利概型的应用例分析“一分耕耘，一分收获”，引导学生树立正确的价值观，弘扬求真务实的精神。在事件的独立性章节，通过合作的案例分析“三个臭皮匠，顶一个诸葛亮”，启发学生的团队合作精神，加强集体主义教育。在二项分布章节，通过设备维护案例分析，说明团队协作能显著提高工作效率。通过泊松分布，启发学生要坚持不懈、锲而不舍、厚积而薄发。在讲到条件分布时，让学生体会透过现象看本质。讲好数学期望的起源故事，培养学生不断探索、追求真理的精神；通过应用数学期望和方差的应用案例分析，引导学生关注社会时政，合理应用数量指标评价社会经济发展水平，培养学生的家国情怀。大数定理以严格的形式表达了大量随机现象中平均结果的稳定性，蕴含着确定性与随机性的辩证统一，反映了量变到质变的转化。中心极限定理表明了不管随机变量序列原来服从什么分布，在一定条件下其和的分布趋于正态分布，体现了哲学中由量变到质变的辩证唯物主义规律，“不积跬步，无以至千里；不积小流，无以成江海”，做任何事情都不要急功近利，每天进步一点点，总有一天能够实现自己的远大目标。极大似然估计告诉我们以发展、联系的观点看问题。通过区间估计领悟唯物辩证法的联系观，坚持两点论和重点论的认识方法，坚定唯物主义信仰。在讲小概率原理时，启发学生认识量变引起质变，“勿以善小而不为，勿以恶小而为之”“锲而不舍、金石可镂”。同时，也体现了偶然性与必然性的辩证关系，“常在河边走，哪有不湿鞋”“祸患常积于忽微，而智勇多困于所溺”。假设检验告诉我们实践出真知，绝对正确或绝对错误的事情很少，要用联系发展的眼光看待问题，思想切不可过于偏执，体现了看问题不可绝对化的唯物辩证法思想。

通过将思政元素（主要包括科学精神、社会责任感、诚信意识、多元文化、哲学思想和创新精神）融入“概率统计”教学中，学生不仅获得知识和技能，还培养了思政素质、道德情操和社会责任感，为人生发展和社会服务奠定良好的基础。

三、课程思政案例

案例教学代表着未来教育方向的一种成功教学方法，于20世纪80年代引入我国。我们在“概率统计”教学中以案例为载体，活化教学内容，完成课程知识的传授、能力培养和价值引领，引导学生探究“概率统计”的实际应用，培养他们解决现实问题的能力和意识。在学习贝叶斯公式时，通过“狼来了”“烽火戏诸侯”等案例的引入，强化诚实守信的意识；通过“三门问题”引导学生打破思维惯性，科学决策。引入抓阄游戏，利用乘法公式科学解释“抓阄不必争先恐后”；引入范进中举的故事，预示做事持之以恒的重要性。应用全概率公式与贝叶斯公式探索种群灭绝问题、敏感问题的社会调查，培养学生理论联系实际的科学精神。利用事件独立性，研究近防炮导弹拦截问题、车间工人协作问题，培养学生的团结协作意识。分析2019年《Nature》中三名科学家质疑P值检验的合理性，引导学生关注“概率统计”前沿理论和发展动态。下面分析“概率统计”中的一些思政案例。

案例1：数学期望的应用（混采检测问题）。对大规模人群（N个人）进行检测，假设每人检测结果呈阳性的概率为p，且各人的检测结果相互独立。有两种检测方法：方法1：逐一检测，需N次；方法2：k人一组，将样本混合后检测，当呈现阳性时，再对某组的样本逐一检测。请评估哪种方法检测效率更高？

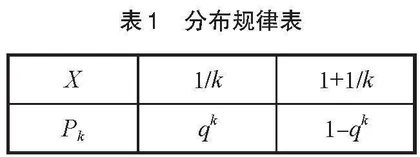
由于每人检测呈阴性的概率为q=1-p，因此将k个人的样本混合后检测呈阴性的概率为qk，呈阳性的概率为1-qk；设k人一组，组内人均检测次数为随机变量X，其分布规律见表1所示。

则X的数学期望公式为：

由数学期望的性质可得，N个人总的检测次数的数学期望为：

如果合理选取k值，则可以使总检测次数的期望小于N。例如，p=0.01时，对于不同的k值，E（X）的值见表2所示。

由此可知，若p=0.01则k取10或11为最佳分组方案，可减少约80％的工作量。再如，当p=0.003时，对于不同的k值，E（X）的值见表3所示。

由此可知，若p=0.003则k取19或20为最佳分组方案，可减少约90％的工作量。

通过对混采检测问题的定量分析让学生认识到混采检测技术的科学性，激发学生科技报国的家国情怀和使命担当。

案例2：中贝叶斯公式的应用（“假阳性”问题）。根据以往的临床记录，某种疾病患者对某项检测呈阳性的概率为0.99，而正常人对该项检测呈阴性的概率为0.999，假设正常人患该疾病的概率为0.0004，现对自然人群进行普查。若某人检测呈阳性，能否判定他患该疾病？

设A表示“检测呈阳性”，B表示“被检测者患该疾病”。由贝叶斯公式，可得检测呈阳性的人员患该疾病的概率公式为：

显然，这个概率比较小，据此不能判定他患该疾病。那么如何进一步提高诊断精度呢？一个很自然的想法是，对首次检测呈阳性的人员进行复查，这时我们将用首次检测呈阳性的人患病的概率替换普通自然人群的人患病的概率，即用后验概率P（B|A）修正先验概率P（B），再应用贝叶斯公式，可得复查呈阳性的人员患该疾病的概率为0.997。因此我们得出结论：复查是降低错检率、提高诊断精度的有效途径。这一案例告诉我们：如果体检时遇到了某种罕见病，不要慌张，赶紧再重新体检一次。

在理解贝叶斯公式的基本思想：大胆预判，小心求证，不断调整，快速迭代的同时，为学生提供一些行为决策的基本原则：保持开放学习的心态，根据新情况不断进行调整，勇于尝试并不断修正，用多元化的视角看待和分析问题。同时培养学生的忧国忧民思想，增强学生服务国家人民的社会责任感，激励学生勇攀科学高峰。

结语

“概率统计”课程思政教学研究的目的是通过课堂教学将挖掘出的思政元素如盐入水般融入教育教学全过程，实现“三全育人”。对“概率统计”课程思政教学实践进行总结，围绕每个知识点深入挖掘紧扣教学内容的思政元素，达到价值塑造、知识传授、能力培养“三位一体”的教学目标，提升学生的实践创新能力和综合素质。

参考文献

［1］教育部关于印发《高等学校课程思政建设指导纲要》的通知：教高〔2020〕3号［A/OL］.（2020-05-28）［2023-04-19］.https：//www.gov.cn/zhengce/zhengceku/2020-06/06/content_5517606.htm.

［2］全国高校思想政治工作会议12月7日至8日在北京召开［EB/OL］.（2016-12-08）［2023-04-19］.https：//www.gov.cn/xinwen/2016-12/08/content_5145253.htm#2.

［3］教育部等十部门关于印发《全面推进“大思政课”建设的工作方案》的通知［EB/OL］.（2022-07-25）［2023-04-19］.https：//www.gov.cn/zhengce/zhengceku/2022-08/24/content_5706623.htm.

［4］陈学慧，李娜，赵鲁涛.将思政元素融入概率论与数理统计“金课”建设与实践［J］.大学数学，2021，37（3）：30-35.

［5］朱柘琍，刘彭.新农科背景下课程思政的探索与实践：以农科“概率统计”为例［J］.教育教学论坛，2022（21）：105-108.

［6］马昕.《概率论与数理统计》课程思政教学改革的实践与探索［J］.高教学刊，2021（3）：135-138.

［7］张艳，陈美蓉，王亚军，等.课程思政理念下概率论与数理统计教学改革的探索与实践［J］.教书育人（高教论坛），2019（12）：80-81.