问题驱动的协方差与相关系数的概念构建

[摘 要] 数学概念对于课程知识体系理解具有重要作用。数学概念教学重在让学生学会构建新概念，而不是单纯学习新概念。以概率论与数理统计中协方差与相关系数两个概念为例，遵循“以问题结构推进教学”的原理，通过国内生产总值与军费支出的关系分析实际案例，提出随机变量关系描述的问题，采用逆向推理得到协方差的定义。在此基础上，进一步深化研究如何描述随机变量关系的强弱及所研究的关系是何种关系，通过一系列层层递进、步步深入、具有内在逻辑联系的问题结构，逐步构建相关系数的定义与内涵。

[关键词] 协方差;相关系数;问题驱动;概念教学

[基金项目] 2020年度国家自然科学委青年基金项目“视图动态变化时的多视图学习方法与应用研究”（62006238）;2020年度国家自然科学委青年基金项目“计算时间域鬼成像目标信息获取能力研究”（62001484）

[作者简介] 陶 红（1990—），女，湖南浏阳人，博士，国防科技大学理学院讲师，主要从事统计机器学习研究。

[中图分类号] O175.14;G642.0 [文献标识码] A [文章编号] 1674-9324（2022）36-0052-04 [收稿日期] 2021-09-27

引言

概率论与数理统计是一门研究随机现象统计规律的学科，研究描述不确定性的数学模型和理论方法，可以应用于科学研究、工程实践、经济管理和人文社科等各个领域，是各大高校理工科专业的数学基础课之一。作为随机数学这一数学分支中学生所接触到的第一门课，“概率论与数理统计”肩负着引导学生逐渐学会利用随机性思维解决问题的重任。不同于以往的确定性数学课程，学生真正掌握概率统计的概念与思想具有一定难度[1，2]。例如，很多学生难以完全理解条件概率、条件分布、协方差与相关系数等概念及其内涵。

数学概念反映了事物在数量关系、结构关系、空间形式等方面的本质属性。数学概念教学要让学生掌握概念的内涵和外延，理解概念间的逻辑关系。因此，数学概念教学应注重概念的构建过程，通过概念的构建过程，对学生进行思维训练。让学生在体会原理的过程中，不仅学会新概念，而且学会利用数学进行科学研究的思维方法。也就是说，数学概念教学不能仅满足于让学生接受、记忆、模仿和练习，更要教会学生自主探究，在自主探究的过程中发展智力、提高科学研究能力[3，4]。

问题驱动教学模式以学生为主体，教师设置一系列问题，引导学生根据问题寻找解决方案，在解决问题的过程中达到教学目标。采用问题驱动的教学模式，有助于帮助学生了解数学概念的深刻内涵，培养数学思维方式，形成应用数学解决实际问题的能力。本文以协方差与相关系数为例，遵循问题驱动的教学原理，以“实例引入—提出问题—分析问题—解决问题”为主线，通过国内生产总值与军费支出的关系分析实际案例，提出随机变量关系描述的问题，并采用逆向推理得到协方差的定义。在此基础上，进一步深化研究如何描述随机变量关系的强弱及所研究的关系是何种关系，逐步构建协方差与相关系数的定义与内涵。

一、提出问题

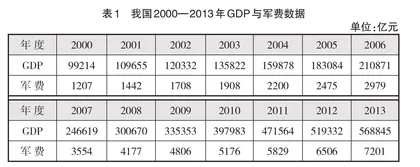
为减少抽象感并激发学生的学习热情，在课程开始时通过“国内生产总值与军费支出的关系分析”这一实例提出问题：如何从数字特征的角度来描述两个随机变量之间的关系。具体地，我国2000—2013年国内生产总值（GDP）与军费支出数据如表1所示。GDP与军费支出均为随机变量，不妨分别记为X和Y，则（X，Y）是二维随机变量，（X，Y）的几何意义是平面上的随机点。通过图1（a）所示散点图发现，14个样本点散落在一条直线附近，随着GDP逐年增长，军费支出也逐年增长。可见，随机变量X与Y之间存在同向变化趋势。从而结合本章主题提出问题：如何从数字特征的角度来描述两个随机变量之间的关系。

二、协方差概念引入

提出问题后，让学生思考如何从数学形式角度进行描述。通过分析，问题转变为找到一个依赖于X，Y的数字量c（X，Y），满足：c（X，Y）≠0，则表示X，Y之间有关系。应如何找到满足上述条件的数字量呢？通常学生难以从正面直接得到解决方案。于是基于逆向思维，引导学生从反面分析。如果存在一个数字量c（X，Y），满足：当随机变量X，Y之间没有关系时必有c（X，Y）=0，那么利用逆否命题则可以得到：当c（X，Y）≠0时，随机变量X，Y之间必有关系。由逆否命题的等价性，c（X，Y）所要满足的条件转换为“当随机变量X，Y之间没有关系时必有c（X，Y）=0”。所谓没有关系即相互独立，由此引导学生回顾已经学习过的数学期望与方差在随机变量相互独立时所具有的性质。当X，Y相互独立时，有E（X，Y）=E（X）E（Y），D（X+Y）=D（X）+D（Y）。

如果令c1（X，Y）=E（X，Y）-E（X）E（Y），c2（X，Y）=

D（X+Y）-（D（X）+D（Y）），那么c1（X，Y）与c2（X，Y）均满足我们所提的要求。应该选择哪一个呢？由于方差本质上是随机变量函数的数学期望，而且计算比数学期望更复杂，因此优先选择c1（X，Y）。

更进一步，为了使定义更简洁，如何将c1（X，Y）=

E（X，Y）-E（X）E（Y）写成1项？如果写成1项，其形式上必定是X，Y的某个函数的数学期望，即需要把

E（X，Y）-E（X）E（Y）变形为X，Y的某个函数的数学期望。由于其中涉及的X，Y交叉项的期望及各自期望的乘积，启示我们变形为E{[X-E（X）]（Y-E（Y）]}，进一步验证确实有E{[X-E（X）]（Y-E（Y）]}=E（X，Y）-

E（X）E（Y）。

此时，询问学生是不是完全得到了协方差的定义。为什么要问这个问题，协方差是利用数学期望定义的，而数学期望的存在需要满足绝对收敛的条件，因此协方差存在的前提是E|[X-E（X）][Y-E（Y）]|<∞。由Cauchy-Schwarz不等式知，当X，Y的方差都存在时，E|[X-E（X）]（Y-E（Y）]|<∞成立。

定义1（协方差）：如果随机变量X，Y的方差都存在，那么称Cov（X，Y）=E{[X-E（X）][Y-E（Y）]}为X，Y的协方差。

由协方差概念的导出过程，易知当X，Y相互独立时，Cov（X，Y）=0;当Cov（X，Y）≠0时，X，Y之间必有关系。另一方面，从定义形式可以看出协方差还可以度量随机点到中心位置的平均偏差。具体而言，对于X，Y的一个容量为n的样本（x1， y1），…，（xn， yn）从总体协方差的定义形式可以得到样本协方差为        （xi-x）（yi-y） 。如图1（b）所示，以（x， y）为原点建立直角坐标系，则当随机点（xi， yi）落入第一、第三象限时，（xi-x）（yi-y）>0;当随机点（xi， yi）落入第二、第四象限时（xi-x）（yi-y）<0。因此，当多数随机点落入第一、第三象限时，样本协方差大于0;反之，协方差小于0。结合图形可以判断，协方差的正负可以从整体上反映（X，Y）的变化趋势是同向还是反向。

三、相关系数概念引入

当协方差的值非0时，则随机变量之间存在关系。按照由浅到深的思路，接下来探讨如何描述关系的强弱程度及是什么关系。向学生提问：协方差的大小能否用来度量关系的强弱程度，能够反映关系强弱的数字量应具有哪些特点？为辅助思考，以GDP与军费支出为例，让学生计算单位分别为亿元和亿万元时的样本协方差。通过计算学生将发现两种情况下的样本协方差之间相差108倍，然而实质上GDP与军费支出之间的关系并不会因金额单位的变化而变化。由此得出结论：协方差不能用于度量关系的强弱程度。事实上，由协方差的定义可验证，对于常数a，b，Cov（aX，bY）=abCov（X，Y）。显然，协方差是一个受量纲影响的数字量。

于是，能够反映关系强弱的数字量应具有不受量纲影响（条件1）的特点。除此之外，还应具有什么特点？提及强弱实质上是为了比较，因此数字量的取值应该是限定在一定范围内（条件2），而且取值随着关系的强弱单调变化（条件3）。

接下来的问题自然就是如何在协方差的基础上定义一个能够满足上述三个条件的数字量。从数学形式上看，所谓消除量纲的影响就是要找到一种方式来消除常数a，b的影响。通常在这里教师都是直接就给出Cov（X，Y）除以                 的方案。事实上，如果仅仅只要消除量纲的影响，还有另一种选择是Cov（X，Y）除以E（X）E（Y）。那为什么用前者而不用后者呢？原因是前者相对于后者在两个方面性质更优：一是数学变形后                   和

都是均值为0、方差为1的随机变量，二是利用Cauchy-Schwarz不等式可以将

的值限定在[-1，1]满足条件2，而                不具备上述性质。

定义2（相关系数），如果          >0，         >0，那么称ρX，Y=                          为X，Y的相关系数。

易验证ρaX，bY=                           =                           =

=ρX，Y，即相关系数确实不受量纲影响。

四、相关系数的意义

从构建相关系数定义的过程可知ρX，Y不受量纲影响且取值在[-1，1]。但仍没有揭示ρX，Y的大小如何反映X，Y何种关系的强弱。为此以常见的二维均匀分布与二维正态分布为例，利用Matlab动画演示当上述两个总体的相关系数从-1增加到1时样本点散点图的变化趋势，以此来发现ρX，Y的大小与X，Y之间关系强弱的对应关系，并探索ρX，Y描述的是X，Y之间的何种关系。具体地，所采用的二维均匀分布与二维正态分布的概率密度函数分别为

和

，

相关系数分别为                         和        =ρ。可以分别通过控制k和ρ的值来调节相关系数的值。通过动画演示让学生发现相关系数描述了随机变量之间线性关系的强弱。进一步，以均方误差为损失函数用随机变量a+bX（a，b为待定常数）近似Y，有如下结论[5]：

0≤minE

a，b {[Y-（a+bX）]2}=D（Y）（1-      ）。

由此可得到如下结论：（1）|ρX，Y|≤1。（2）|ρX，Y|越大，则a+bX与Y之间的均方误差越小，即X与Y之间的线性关系越强;反之，则X与Y之间的线性关系越弱。并且，结合图形（图2）可知，当ρX，Y>0时，X与Y整体上具有同向变化趋势;当ρX，Y<0时，X与Y整体上具有反向变化趋势;当ρX，Y=0时，X与Y之间没有线性关系，称为X与Y不相关。