省级统一命题背景下初中数学复习教学的思考与实践

摘    要：省级统一命题意味着标准评价的统一，即依标命题.教师需要切实理解课程标准，着力构建以提升能力、发展素养为锚点的复习课堂教学新范式.在复习教学中，教师可系统梳理知识，使学生“温故知新”，引导学生学会综合运用知识解决问题，做到“融会贯通”. 教师需要以一般观念为统领，进行单元整体教学设计，梳理相关知识的内容逻辑和教学逻辑，帮助学生完善知识结构体系.教师还要厘清作业设计的误区，设计完整的训练系统，并结合多元的评价，推动学生高效学习，进而实现核心素养的真正落地.

关键词：单元整体设计；复习教学；初中数学

初中学业水平考试省级统一命题需要依据义务教育课程标准，坚持素养导向、知识与能力并重的基本原则，以必备知识为载体，着重考查核心素养和关键能力.省级统一命题意味着评价标准的统一，即依标命题，这对教师和学生都提出了挑战.正如《中共中央  国务院  关于深化教育教学改革全面提高义务教育质量的意见》中指出的那样，需要切实“引导教师深入理解学科特点、知识结构、思想方法”，进一步理解课程标准，理解“教—学—评”一致性的内涵.因此，当务之急是着力改变复习教学的基本模式，如“罗列知识点（美其名曰“画思维导图、知识结构图”）+分析题型套路+刷题”的模式等，使课堂教学从“教师中心”“知识中心”转变为“核心素养导向”，着力构建以提升能力、发展素养为锚点的数学复习课堂教学新范式.

一、梳理·运用：构建联系，提升能力

提升能力、内化素养，既是复习（本文所指的复习是学段末的综合复习）的途径，也是复习的目的.复习时，教师既要系统梳理知识，使学生“温故知新”，也要引导学生学会综合运用知识解决问题，做到“融会贯通”.也就是说，复习教学既要引导学生构建数学知识之间的联系，更要让学生透彻理解数学的本质.

（一）梳理的目的是建立知识之间的关联

当下复习课教学中流行的梳理，只停留在基础知识的罗列层级，常见的形式是知识列表、填空或思维导图等，虽也能呈现出一定的结构特征，但这种结构比较松散，追求的只是知识的覆盖.这种梳理方式只适用于章新课结束的复习，即在章新课结束时，教师引导学生通过梳理使所学知识结构化，明晰该章的学习重点和难点.而中考前总复习中的梳理，应该是梳理知识之间的关联以及它们是如何关联的.实际上，关联两个或多个不同知识的纽带，往往是它们最为核心的部分，因此通过梳理，既可以实现透彻理解数学本质的目的，也能使知识具有整体性和良好的结构.

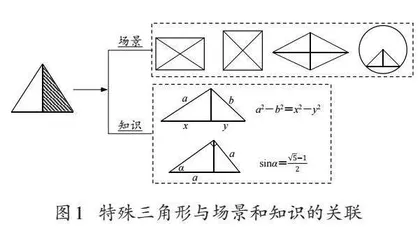
情形一：在复习A知识（知识群）时，建立知识A与知识B或者场景C之间的联系.例如，特殊三角形与场景的关联有：（1）矩形的两条对角线把矩形分割成4个直角三角形和4个等腰三角形；（2）正方形的两条对角线把正方形分割成4个等腰直角三角形；（3）菱形的两条对角线把菱形分割成4个等腰三角形和4个直角三角形；（4）垂径定理就是等腰三角形与圆（场景）结合的结果；等等.特殊三角形与知识的关联有：（1）与一般三角形的关联（如“投影”）；（2）与特殊三角形的关联（如“黄金比”）；等等.特殊三角形与场景和知识的关联如图1所示.

通过场景关联，学生能熟悉知识A在场景B中的位置关系和数量关系（特殊性质），增加学习体验，积累学习经验，为未来解题提供熟悉的环境和有用的经验.通过知识关联，学生能更为深刻地理解对象的性质.如直角三角形与一般三角形的关联，其结果“a2－b2＝x2－y2”反映的是：通过投影的方法可以把一个二维结构“a2－b2”转化为一维结构“x2－y2”.因此，可以通过实数运算解决问题.

情形二：在复习A知识（知识群）时，可以建立与A相关的知识网络.透过知识网络，容易发现单元的重点和难点，从而凝练出统摄单元的一般观念.例如，梳理“方程”单元的知识结构（如图2所示）可知，统摄该单元的一般观念是消元和降幂思想.这个一般观念传递的是一种认知信念：不论是多元问题还是高次问题，都可以化归为“一元”或者“一次”的问题来解决.它也意味着一种行动指南：多元问题需要消元，高次问题需要降幂.同时，它又体现为一种知识系统：方程是按照一定的序（“元”和“次”）构建起来的一个有序结构.因此，它还蕴含着一种思维视野：从一元到多元、从一次到高次、从特殊到一般.由此，我们就可对一元二次方程的不同解法形成理性的价值判断：配方法的价值在于导出求根公式；求根公式为求解一元二次方程提供一般方法；而因式分解法则是一种解决问题的思想方法［1］.

情形三：在复习A知识（知识群）时，关键在于建立知识A与场景B之间的联系.确立关联知识A和场景B的纽带是关键，也就是说，知识A和场景B之所以关联是需要有“牵线者”的.一般而言，这个“牵线者”一定是揭示知识A和场景B的最为核心的部分，譬如等腰三角形的“三线合一”和圆的“直径对直角”，有时候二者关联后“生成”的新的基本图形也至关重要.例如，课题“等腰三角形遇见圆”，关键在于等腰三角形是如何“遇见”圆的.也就是说，这个“牵线者”是谁、是如何“牵线”的等问题，是关联等腰三角形（知识）和圆（场景）的关键.如图3所示，△ABC是等腰三角形（AB＝AC），由左侧虚线框中的图形可知：①中的辅助线AD就是关联等腰三角形和圆的纽带，它既是等腰三角形的“合一”三线，也是圆的“直径对直角”的直角边；②中由线段DE能生成新的等腰三角形EDC；③中角平分线AD和等腰三角形在场景内关联，形成充要条件“BD＝DC[⇔]∠BAD＝∠CAD”，事实上，还有更为深刻的结论“AB·AC＝AE·AD；BD2＝DE·DA”；等等.

情形四：对试题进行关联、统整和结构化研究.

题1：在△ABC中，AD⊥BC于点D，求证：AB2－AC2＝BD2－DC2.

题2：四边形ABDC的对角线AD⊥BC于点E，求证：AB2－AC2＝DB2－DC2.

题3：点P是矩形ABCD内一点，求证：PA2＋PC2＝PB2＋PD2.

题4：点D是等腰直角三角形ABC的斜边BC上一点，求证：BD2＋DC2＝2DA2.

题5：点D是等腰三角形ABC的底边BC上一点，求证：AB2－AD2＝BD·DC.

对这5道题作分析，可以整理为如图4所示的结构图，下面具体分析.把题1作为一个基本结论，则题2只要两次利用题1结论（AB2－AC2＝BE2－EC2；BD2－DC2＝BE2－EC2）即可求证.

题3只需要过点P作两条垂直于边的线段EG和FH，四边形EFGH满足题2的条件，因此EH2＋FG2＝EF2＋HG2.显然，EH＝PA，EF＝PB，FG＝PC，GH＝PD，所以题3得证.

题4有三种证明方法：一是将等腰直角三角形ABC补全为正方形ABEC，则根据题3结论，有BD2＋DC2＝DA2＋DE2，显然，DE＝DA；二是受题3启发，过点D作DE⊥AB于点E，DF⊥AC于点F，即图4-5的方法，则BD2＋DC2＝2（DE2＋DF2）＝2DA2；三是将4-6作为基本图形，由题5的结论推出，因为AB2－AD2＝BD·DC＝[12]［（BD＋DC）2－（BD2＋DC2）］＝[12]BC2－[12]（BD2＋DC2）＝AB2－[12]（BD2＋DC2），整理即得.

（二）运用的关键是在新场景中解决问题

复习的目的是提升学生综合解决问题的能力，表征为学习迁移. 学习迁移是已经获得的知识和经验对解决其他问题所产生的影响，本质就是认知结构在新条件下的重新构建，旨在使学习者形成对知识的深刻理解.因此，复习教学需要关注知识和经验在不同应用场景中的迁移.也就是说，复习知识A不能仅仅在A场景中应用（这样做固然可以提升对知识A的熟练程度，但对提升学生解决问题的能力作用不大），而必须在场景B、场景C等不同的场景中应用.学生如能在新的场景中用知识和经验解决问题，则说明其能力已经得到了提升.

例1［2］：在△ABC中（图略），AC＝BC，以AB为直径的⊙O分别交BC，AC于点D，E．求证：[BD]＝[DE]．

显然，连接等腰三角形ABC和⊙O的纽带是线段AD，通过“三线合一”知AD平分∠BAC，因此本题的证明思路就非常清晰了．

例2：如图5所示，已知△ABC∽△ADE，BD⊥BC.求证：[EB2-ED2CA2-CB2=BD2AB2]．

显然，在三角形中，关联结构CA2－CB2和EB2－ED2的纽带是三角形的高线.因此，分别作△ABC和△BDE的高线CG和EH，则CA2－CB2＝AG2－BG2，EB2－ED2＝BH2－DH2．

所以[EB2-ED2CA2-CB2=BH2-DH2AG2-BG2]＝

[BD∙（BH-DH）AB∙（AG-BG）]，

因此问题转化为证明：[BH-DHAG-BG]＝[BDAB]．

根据等比定理，只需要证：[BHAG]＝[BDAB]．由△ABC∽△ADE，得[ADAB=AEAC]．

可以证明△ADB∽△AEC，所以∠ABD＝∠ACE＝∠BCG，[BDAB=ECAC]．

所以∠BCE＝∠ACG，所以[BDAB=ECAC=ECsin∠BCEACsin∠ACG=HBAG]．

例3：（2024年1月杭州市拱墅区期末卷）如图6所示，四边形ABCD内接于⊙O，对角线AC平分∠BAD，连接BD交AC于点E．求证：AC2＝BC2＋AB·AD．

证明：由图3-③的结论，知AB·AD＝AE·AC，BC2＝CE·CA．

因此AC2－AB·AD＝AC2－AE·AC＝CE·AC＝BC2．

所以AC2＝BC2＋AB·AD．

例4：（2024年1月杭州市西湖区期末卷）如图7所示，在△ABC中，AB＝AC，点P为线段BC上任意一点（P与B，C不重合），连接AP.若AB＝m，AP＝n，请用含m，n的代数式表示BP·PC，并说明理由．

解：由图4-5的结论，知AB2－AP2＝BP·PC，即BP·PC＝m2－n2．

不难发现，有了知识间的联系分析，学生就能熟门熟路地解决问题.这样既能提高解题的准确率，也能缓解心理焦虑.

二、单元·整合：形成结构，发展素养

基于单元设计的复习教学，主要是指从模块入手，设计超越模块的任务，形成单元整体教学，帮助学生完善知识结构体系，实现核心素养的真正落地.因此，一般观念是单元整体教学的“魂”.单元整体教学的基本结构如图8所示.

例如“函数”单元复习教学设计，先要梳理出指导“函数”复习的一般观念，即需要梳理“函数”教学的内容逻辑和教学逻辑，具体如下.

其一，函数性质的研究.函数学习的核心是研究函数的性质，初等函数的性质一般包括单调性、对称性、最大（小）值和周期性等，但是对称性等性质都是由单调性的变化而引起的，如函数先增后减会形成最大值，周期性则是在不同的区间内重复同样的单调性，因此，研究函数的单调性是第一要务.研究函数单调性的数学工具是导数，但初中阶段未安排学习，因此需要创造直观工具.

其二，研究工具的创造.数学中有一种常用的方法就是把研究对象的未知空间通过映射，投影到已知空间中，然后在已知空间中研究清楚了，再进行逆映射，这样就能弄清楚这个未知空间对象的性质.函数是变量y的变化规律由变量x唯一决定的数学模型，即x和y总是成对出现，因此空间A中的元素可以用有序的数对（x，y）表示，而该有序数对的直观是平面直角坐标系的一个点，这样就可以把空间A中的有序数对（x，y）投影到空间B（平面直角坐标系）中，得到函数的图象，接下来就可以借助函数的图象研究函数的性质.