从解构到建构：基于理解的物理概念教学

摘    要：概念是物理教学的基础，它与许多相关知识、方法、技能、观念等联系在一起，进而组成学科大概念。从整体上理解概念，要先对概念进行解构，再在理解学生的基础上，按照知识发生发展的规律以及学生的认知规律进行概念建构。具体教学中，教师可依据时间表、线路图、概念核心对相关概念进行解构，然后依据学生学习概念的物理现实和思维断档处寻求学习支持条件，最后通过问题情境、抽象概念、数学表达、实验探究四步引导学生建构概念，帮助学生在概念学习中提升物理学科核心素养，落实立德树人根本任务。

关键词：概念理解；概念解构；概念建构；物理教学

理解物理概念是立教之本，讲不清基本概念，其他任何研究都无从进行。但当下，由于教师对物理概念理解不到位、对物理规律理解不深刻，导致教学活动不得要领、教学效率低下的情况仍普遍存在。为达成有效甚至高效教学，教师不仅需要理解物理概念，还需要理解教学规律和学生认知，从而科学、合理地对物理概念进行解构与建构。

一、从解构到建构的概念教学框架

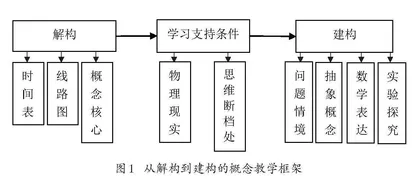
物理概念不是孤立存在的，而是与许多相关知识、方法、技能、观念等联系在一起，进而组成学科大概念。因此，从整体上理解概念，需要对概念进行解构，即对与之相应的学科大概念进行梳理，对知识本质进行提炼，聚焦核心素养，找出概念的核心所在。物理教学中，对概念的解构是为了建构概念，而建构概念离不开学生的参与，因此，教师需要理解学生，并通过分析学生学习概念的物理现实和思维断档处，寻求学习支持条件。只有理解了概念、理解了学生，教师才能按照知识发生发展的规律以及学生的认知规律引导学生进行概念建构。笔者经过长期实践，提炼出从解构到建构的概念教学框架，具体如图1所示。

对图1需要作三点说明：（1）解构是从物理学科的视角理解概念，通过解析大概念的学习时间表、知识发生发展的线路图，寻找概念的核心所在，从而明晰概念“是什么”；（2）学习支持条件是从学生的视角理解概念，通过对学生学习概念的物理现实和思维断档处进行分析，从而明确概念“如何学”，并为建构提供支持；（3）建构是从教学的视角理解概念，将概念解构后，结合学习支持条件，按照“问题情境—抽象概念—数学表达—实验探究”路径组织教学，从而确定“怎么教”。

二、从解构到建构的概念教学实践

速度是描述物体运动的重要物理量，是运动学中的核心内容，在“如何准确描述物体运动”中有着奠基作用。速度是其他物理量的基础，如动量、能量、加速度等都与物体的速度有关。学习速度，学生能加深对“物理量的变化”的认识［1］。下面，笔者以“速度”概念为例，具体阐述如何对物理概念进行解构与建构。

（一）“速度”概念的解构路径

从物理学科的视角出发，教师可解析构成“速度”概念学习的时间表，以及知识发生发展的线路图，寻找“速度”概念的核心所在，引导学生达成对“速度”概念本质的理解。

1.时间表

物理概念的学习只能是以时间先后顺序展开，概念学习的时间顺序构成了概念学习的时间表。时间表既能揭示概念发生发展的逻辑顺序，也能揭示学生学习概念的认知顺序。人教版普通高中教科书《物理》（以下简称“人教版《物理》”）必修第一、二册“速度”学习时间表如表1所示。

从表1可以看出：速度是运动学的基础，与许多物理量有关；“速度”概念的学习是一个比较长的过程，其教学安排不能一步到位。

2.线路图

线路图能揭示知识之间的联系。要把握知识发生发展的脉搏，就需要理清知识发生发展的线路图。例如，在描述物体运动时，我们需要明确以下几点：（1）研究对象是什么（质点）；（2）用什么工具来研究（参考系）；（3）如何描述运动的快慢（速度），而为了进一步精确描述物体运动的快慢，需要引入平均速度和瞬时速度的概念；（4）如何描述速度变化快慢（加速度），以及有哪些物理模型和数学描述的方法。这一逻辑线索构成了“速度”概念发生发展的线路图，具体如图2所示。

从图2可以看出，“速度”概念处于核心地位，可以毫不夸张地说，理解了速度，就理解了机械运动。

3.概念核心

概念核心反映了概念的本质属性。“速度”概念的核心是描述物理量的变化，是用位移与时间的比值来刻画运动的快慢。

为了描述物体运动的快慢，物理学用位移与发生这段位移所用时间的比（即速度）来表示。为了进一步精确描述物体运动的快慢，又引入平均速度和瞬时速度概念。平均速度表示某段时间内，物体平均运动的快慢程度；瞬时速度表示在非常非常小的时间跨度内的平均速度，即物体在运动时间趋于0时的平均速度。

速度是矢量，既有大小，又有方向。速度的大小叫作速率，用[ΔxΔt]表示，速度的方向与位移的方向一致。建立速度—时间图像以及位移—时间图像后，我们就可以用数学工具精确描述速度了。

（二）“速度”概念的学习支持条件

教师的教是为了学生的学，这表明从概念解构到概念建构，教师还需要分析学习支持条件。如何分析概念的学习支持条件呢？笔者认为，可结合学生的物理现实，估计其思维可能出现的断档，引导学生更好地实现建构。

1.物理现实

学生头脑中已有的物理认知结构又称为物理现实，它体现了物理知识之间的内部关联。物理现实包括物理知识、物理经验、物理方法、物理观念、物理规律和物理核心素养等，是学生学习物理概念的基础。在教学中，我们可以分析具体物理现实的上位概念、下位概念、平行概念，以及其中蕴含的思想方法和核心素养。例如，对于“速度”概念，我们可以列出如下物理现实清单。

（1）上位概念：机械运动，比值计算。

（2）下位概念：平均速度、瞬时速度，速度—时间图像，初中阶段学习过的“速度”概念。

（3）平行概念：位移，时间，加速度。

（4）思想方法：数形结合思想，微元法与极限思想。

（5）核心素养：运动观念，科学思维。

这些物理现实清单是学习速度的基础，以此组织教学，能帮助学生全方位、多角度地理解“速度”概念，形成“运动观念”。

2.思维断档处

在物理大概念网中，有些认知结构与学生已知的认知结构关联性较弱，即概念网络中节点不连续就会出现认知断档，继而出现思维断档。思维断档处往往是学生容易出错的地方，同时也是教学必须突破的关键所在。抓住概念网中不连续的节点，就抓住了教学难点。反之，教学难点的确定就会出现偏差。学生在初中阶段就对物体运动的快慢有一定的认识，但在比值定义、概念的建构方面还较为薄弱，主要有如下两个思维断档处。

其一，从初中的标量进阶到高中的矢量来认识“速度”概念，是学生思维上的第一个断档处。这是因为，学生在初中阶段学习的“速度”概念是路程与时间的比值，而高中阶段学习的“速度”概念是位移与时间间隔的比值。

其二，从平均速度过渡到瞬时速度，学生首次接触到极限思想，这是第二个思维断档处。学习瞬时速度时，由于涉及极限思想，其解释需要用到数学中的微积分知识，而此时学生尚未接触过微积分，因而存在理解上的困难。比如，常常有学生认为某一时刻物体的时间间隔和位移都是0。导致出现这种错误认识的原因是，学生在认知上把物体固定在一个点，其根本是缺乏极限思想。

因此在教学时，教师应从学生的已有知识出发，引导学生自主学习、科学探究，从而建构速度、平均速度、瞬时速度等概念。

（三）“速度”概念的建构路径

物理概念的习得过程，往往要经历“观察—比较—概括—抽象—表征—迁移应用”的科学思维过程［2］。因此，物理概念的建构，也应从实际背景出发，抽象出物理概念，再用数学工具进行表达，最后用实验验证。按照这一逻辑，笔者提炼出概念建构的路径，具体如图3所示。

1.问题情境（真实情境）

物理概念是对物理现象和物理事实的科学抽象，它能够用来描述物理过程和状态的本质，科学准确的物理概念是探索物理规律和解释物理现象的有力工具［3］。因此，物理概念的建立往往是从真实问题（基于学生的物理现实的真实问题）开始的。

在“速度”概念的教学中，笔者设计了如下情境与问题。

真实情境：张老师驾车从杭州第十四中学青山湖学校到杭州第十四中学凤起校区，开启了北斗高清导航。到终点后，导航上显示39千米、48分钟（图略）。

问题1：39千米的含义是什么？（路程，不是位移）

问题2：根据39千米和48分钟，可以计算什么？（速度）

问题3：起点与终点之间连接的直线有何意义？（直线距离，对应位移）

问题4：如果行驶了30分钟，你能否预测汽车的位置？

这些问题是基于学生的物理现实而设计的。通过这些问题，教师可引导学生在分析物体位置变化快慢的描述中，形成强烈的认知冲突，颠覆初中时形成的认知，从而明确应该用位移与时间的比值作为速度，发展物理观念核心素养。

2.抽象概念

物理概念是从物理学视角形成的对物理相关知识、观念等的基本认识。物理概念源于物理实际，抽象于感性认识，应用于生活实践。在物理概念的学习中，我们可以通过观察、类比、演绎推理等方法，从具体物理现象中抽象出概念。

为了从真实情境中抽象出“速度”概念，笔者继续提出如下问题。

问题5：张老师在这段行程中，要在高速公路上行驶一段时间。高速公路上有区间测速，它测量的是什么速度？（平均速率）

问题6：在行驶过程中，张老师手机界面显示的是什么速度？（瞬时速度，这个瞬时速度是由卫星计算车辆在极短时间内的位移与时间间隔的比值得出的）

问题7：张老师在里程为10千米的区间测速段行驶，区间车速大于120 km/h为超速。张老师用了6分钟通过该测速区间，那么他的区间测速超标吗？该区间某时刻汽车的瞬时速度可能超过120 km/h吗？（区间测速测的是平均速率，不超标；某时刻汽车的瞬时速度有可能超过120 km/h）

对这些问题进行思考，学生可建构平均速度与瞬时速度的概念，发展科学思维核心素养。

3.数学表达

物理学是一门实验科学，也是一门遵循逻辑推理的科学，物理学的发展必须借助强有力的数学工具。数学是物理的表达形式，数学能以简洁的语言刻画物理世界的基本结构，精确表达自然规律。因此，形成物理概念后，用数学表示是必不可少的，这也是培养科学思维的必由之路。

在“速度”概念的建构中，数学表达体现在三个方面：一是速度的定义，即位移与时间间隔之比，表示为[v=ΔxΔt]；二是用速度—时间图像直接呈现速度随时间变化的规律；三是位移—时间图像，割线的斜率表示平均速度，某点切线的斜率表示该点的瞬时速度。

以瞬时速度的建构为例，可设计如下问题进行教学。

问题8：如图4所示，在匀变速运动中，AB段内物体运动的平均速度如何表示？（过A点的割线AB的斜率）

<I：＼2023教学月刊社＼2024年＼2024教学参考＼2024-5＼教学参考2024-5内芯＼Image＼切线.pdf>

图4

问题9：在物理学科中，当运动时间间隔非常小时，物体运动的平均速度就可以认为是瞬时速度。你能借助图4的几何表示作出解释吗？（缩短与A点的时间间隔的割线AC，其斜率反映的是在线段AC段内物体运动的平均速度，进一步缩小时间间隔，当时间间隔非常非常小时，过点A的割线就会逼近切线，而切线的斜率准确表示了t0时刻的运动快慢，即瞬时速度）

问题10：请从数学的角度，说说你对瞬时速度的认识。（从数学角度看，导数的几何意义是某点切线的斜率，从这个意义上讲，瞬时速度就是位移对时间的导数，即[v=x（t）]或[v=limt→t0x（t）-x（t0）t-t0]。借助数学表达[v=limt→t0x（t）-x（t0）t-t0]，学生能很好地理解瞬时速度的本质，即在极短的时间内描述物体位置变化的快慢）