基于模型构建实现认知结构化的高中物理复习教学

摘    要：模型构建是对物理问题、情境的各要素、多信息进行分析、比较、判断，可帮助学生在新旧知识间建立联系、形成结构。基于模型构建实施复习教学时，教师需要根据对知识结构化的分析，研究学情并聚焦学生的认知结构化，提炼实施路径。在具体的教学中，教师可通过提炼主问题、进阶思维、整合图示等方式，在模型构建中呈现知识结构，在微项目推进中深化思维结构，在逻辑关联中升华观念结构，引领学生达成认知进阶，实现认知结构化。

关键词：模型构建；进阶复习；认知结构化

*本文是浙江省教育科学规划课题“结构化教学：指向核心素养的高中物理课堂实践研究”（课题编号：2024SC221）的阶段性研究成果。

2023年6月浙江高考物理选考压轴题三个设问（原题略）梯度明显。对我校参加该次高考的学生进行调研后，笔者发现在该题的解答中，学生对带电粒子在磁场中运动的情境比较熟悉，已形成求解问题的基本思路“定圆心，画轨迹，找几何关系”，但对三个问题的解答情况各异：第一问是简单几何关系的寻找和求解，有95.26%的人回答正确；第二问有37.11%的人回答正确，其中绝大多数采用几何关系求解，只有3人采用了动量定理来分析；第三问只有13人（占比为6.28%）考虑到磁场变化后带电体受到变力作用，试图从洛伦兹力的分量方面来考虑，并采用动量定理求解，但只有2人拿到了满分。实际上，学生对物体受到与速度成线性关系的变力作用下的运动并不陌生，比如空气阻力、洛伦兹力、电磁感应中的安培力等，但由于没有对此类问题的受力特点和求解策略作系统的归纳总结，没有形成系统的认知结构，从而不能正确地迁移应用知识。《普通高中物理课程标准（2017年版2020年修订）》强调“重视以大概念为核心，使课程内容结构化……促进核心素养的落实”，因此在日常的复习教学中，教师可从模型构建的角度，逐步引领学生达成认知进阶，进而实现认知结构化。

一、从知识结构化到认知结构化

结构化意味着联系、关联。从认知加工过程来看，知识结构化是将累积的知识进行关联并形成具有良好层次结构的知识体系，而认知结构化是从具体知识中提取出认知思路（思维结构化）和基本观念（观念结构化），将更多具体知识关联起来，形成良好的认知结构［1］。

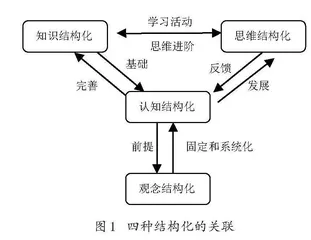
知识结构化是认知结构化的基础。学习是学生主动地在头脑内部构造认知的过程，学习的结果不只是针对某种刺激作出的特定反应，而是在头脑内部重建认知图式，图式的形成和变化是认知发展的实质［2］。学习活动的创设，可以促使思维进阶发展，因此，思维结构化是认知结构化的反馈。认知结构化又是观念结构化的前提，观念的形成会促使认知结构固定和系统化。从知识结构化到认知结构化的进阶，伴随着思维结构化和观念结构化的发展，这又促使知识结构更加完善系统［3］。四者的关系如图1所示。

二、基于模型构建实现认知结构化的复习教学路径

模型构建即对物理问题、情境的各要素、多信息进行分析、比较、判断，它是一种复杂的、高级的认知过程。通过模型构建，学生可以在新旧知识间建立联系、形成结构，理解知识所蕴含的基本思想方法。由此，学生就能运用知识和方法灵活且有条理地解决真实情境中的问题，对知识的意义有正确的判断并形成更深、更广的结构化知识。模型构建的基本路径如图2所示。

在复习教学中，教师可呈现系列情境化试题，让学生在主体活动中，对物理问题、情境的各要素、多信息进行分析、比较、判断，通过联想、调动、激发以往的知识经验，构建出自己的知识结构。同时，教师可引导学生进行模型构建，通过分析、比较从系列问题中确定主问题，然后以主问题为引领去同化知识结构。具体而言，在依据主问题设计推进若干个微项目、解决子问题的过程中，教师需要引导学生做到如下几点：（1）通过模型构建实现知识关联；（2）通过科学推理，对学习内容进行深度加工，厘清逻辑层次，理解本质属性，全面把握知识的内在联系；（3）通过科学论证，寻找证据，证明观点，提升观念；（4）通过质疑创新，实现变式迁移，从而使学生获得更高层次的知识经验，形成更深刻的知识结构，促使思维结构化的形成。在复习课尾段，师生可共同绘制知识框图、思维导图等，利用图示整合手段，在逻辑关联中优化观念结构，使学生的认知结构进一步深化发展，进而能够迁移应用。基于模型构建实现认知结构化的复习教学路径如图3所示。

三、基于模型构建实现认知结构化的复习教学策略

（一）提炼主问题，在模型构建中呈现知识结构

主问题在教学中能“牵一发而动全身”，支撑起整个复习教学活动，它是课堂活动的导火索、助推器和黏合剂。一个高度概括、基于真实情境、贯穿一节课始终的主问题，能不断引领学生进入深度学习，使其基于主问题构建知识结构，分析问题、解决问题，从而提升学科素养和关键能力。因此，设计和实施复习教学的首要任务就是提炼主问题。

【主问题提炼】在力f = kv作用下的运动

［情境］视频展示热气球运动。

师：热气球上升受到哪些力的作用？

生1：重力和浮力。

生2：气球还会受到空气阻力。

师（追问）：同学们从什么方面感觉到有空气阻力？空气阻力可能与哪些因素有关？

生3：骑车时由于人与空气有相对运动，可以感受到空气阻力；而且与走路时相比，骑车时感受到的空气阻力更大，因此空气阻力应与运动速度有关。

生4：战斗机快速停下来前要打开减速伞，主要是为了增大与空气的接触面积，因此空气阻力与接触面积有关。

设计意图：通过视频让学生感知真实情境，引导学生主动根据生活经验和已有认知思考问题，树立正确的运动观和相互作用观，为认知结构化奠定基础。同时，通过师生、生生探讨，明确主问题。

【情境化试题呈现】2013年浙江高考物理卷第19题

总质量为460 kg的热气球，从地面刚开始竖直上升时加速度为0.5 m/s2。当热气球上升到180 m时，以5 m/s的速度向上匀速运动。若离开地面后热气球所受的浮力不变，上升过程中热气球总质量不变，重力加速度为10 m/s2，下列说法正确的是（        ）

A.所受的浮力大小为4 830 N

B.加速上升过程中所受的空气阻力不变

C.从地面开始上升10 s后的速度大小为5 m/s

D.以5 m/s匀速上升时所受的空气阻力大小为230 N

设计意图：让学生在分析并利用牛顿运动定律求出浮力大小的过程中，根据加速度、上升高度、速度三个数据发现气球并没有做匀变速直线运动，由此形成认知冲突，进而重新构建条件模型“热气球运动过程中会受到空气阻力，阻力大小与速度相关”，再结合气球受力分析构建过程模型“加速度逐渐减小的加速运动，随后做匀速运动”，问题便迎刃而解了。

【真实问题抽象】

在地面上以初速度v0竖直向上抛出一小球，经过一段时间小球落回抛出点，其速率为v1，假设小球在空中运动时所受空气阻力与小球运动的速率成正比，小球在运动时速率随时间如何变化？能否画出v-t图像？

设计意图：引导学生进行动力学分析，展示学生分析成果，推动学生在交流探讨中树立正确的运动观和相互作用观。

师（追问1）：小球从抛出到落地过程中阻力做了多少功？

设计意图：引导学生从能量的角度思考问题，树立正确的能量观。

师（追问2）：小球从抛出到落地过程中运动的时间t为多少？

设计意图：使学生发现无法用匀变速运动规律求时间，引发认知冲突，再引导学生通过认知关联重新构建模型，寻求思路。关联1：冲量是力在时间上的积累，运用动量定理可以求解时间。关联2：微元法（化变为不变）可以处理变加速运动。进一步推理可发现速度对时间的累加为位移，由此在思维冲突中形成问题分析的基本策略，即动量定理+微元法：“上升阶段：[-mgt1-kv-t1=-mgt1-kh=0-mv0]，下降阶段：[mgt2-kv-t2=mgt2-kh=mv1-0]。”

师（追问3）：假设小球在空中运动时所受空气阻力与小球运动速率的平方成正比，那么运动的时间t怎么求？

设计意图：让学生通过分析发现速率的平方对时间累加没有意义，发现高中阶段暂时没法处理这一问题，从而对此类力的特性有更进一步的理解。

师（追问4）：将小球换成一质量为m、电阻为r的导体棒，让其沿一倾角为θ、长度为L的光滑金属轨道以速度v0 滑动，金属轨道上端连一电阻R。导体棒上滑到顶端后回到出发点时的速率为v1，求运动的时间t为多少？

设计意图：呈现学生熟悉的电磁阻尼模型，引导学生通过将安培力[F=B2L2vR+r]与空气阻力f = kv比较，将安培力冲量[I=B2L2v-R+rt=B2L2R+rx]与空气阻力冲量[I=kv-t=kh]比较，形成结构化的知识关联，明确此类问题的受力特征和求解策略，初步达成知识的结构化。

师（追问5）：高中阶段学习过的力中，还有哪些与速度大小成正比？它们是否也有同样的特性？

设计意图：引导学生在空气阻力和安培力的启发下，归纳出带电粒子在磁场中受到的洛伦兹力，分析这些力的共性和个性（大小都与速度成正比，空气阻力和安培力方向与速度相反，而洛伦兹力方向与速度垂直），然后在模型构建中再次思考主问题：在力f = kv作用下的运动。从运动和受力特性出发，使学生自然地提出疑问：处理洛伦兹力时是否也具有同样的求解思路？

（二）进阶思维，在微项目推进中深化思维结构

对主问题进行深度剖析，围绕主问题设置微项目、子问题，借助情境化、启发性的关联素材，让不同水平层级的学生都能找到与自己水平、能力比较匹配的微项目，从而主动参与、积极思考并交流讨论。“阶”是学生认知过程中的“立足点”，正是一个个连续的“阶”将知识、复习的起点和终点有序连接起来，实现认知过程的“进”。进阶复习，就是引导学生根据进阶点，参与结构化的知识复习，建立复习内容的内在逻辑结构与层次，从而逐渐达到深度学习的状态，提升思维的结构化。

【微项目一：有阻尼的曲线运动分析】

例1：在考虑空气阻力的情况下，一小石子从O点抛出沿轨迹运动，其中P是最高点，Q是落地点。若空气阻力大小与瞬时速度大小成正比，则小石子竖直方向分运动的加速度大小（        ）

A. O点最大   B. P点最大

C. Q点最大   D. 整个运动过程保持不变

师（追问1）：上升和下降的时间相同吗？

师（追问2）：若石子抛出时速度为v0，与竖直方向的夹角为θ，经过时间t运动到最高点，求上升的最大高度。

师（追问3）：若运动到最高点，速度变为v，则此过程中石子的水平位移为多少？克服阻力做功多少？

设计意图：从有阻尼的直线运动到有阻尼的曲线运动，从一维运动到二维运动，是学生思维的有序进阶，符合学生的认知发展。在学生已有认知的基础上，通过知识迁移应用，更容易引导学生利用运动的合成与分解处理问题，将运动从二维降为一维，在变式中构建物理模型，进一步培养科学思维能力、深化思维结构。同时，可使学生在交流讨论中理解受力本质，树立正确的相互作用观，巩固认知结构。

【微项目二：迁移进阶——洛伦兹力作用下带电体的运动】

例2：质量为m，带电量为q的物块放在倾角为[α]的斜面上，与斜面间的动摩擦因数为μ。设整个空间放在匀强磁场中，磁感应强度为B，方向垂直纸面向里，物块从静止开始运动，经过时间t脱离斜面。