培育综合素养的初中数学跨学科项目式学习探究*

摘    要：跨学科项目式学习强化不同学科内容的整合，突出学科思想方法和探究方式的学习，强调知行合一、学思结合，倡导做中学、用中学、创中学，可有效培育学生的综合素养.在数学教学中，教师需要聚焦核心素养以发展综合品质，聚焦真实问题以整体联动设计，引导学生在辩论激活思维、自主萌发创新，个体创意设计、集体共同研究，分层自选作业、具化外显成果的过程中，实现进阶式学习，提升综合素养.教师还需注重价值导向以打破学科壁垒，提供支架助学以引导学生持续探究，重视学科生长并以单学科的深研助力跨学科问题解决.

关键词：跨学科项目式学习；综合素养；初中数学

《义务教育课程方案（2022年版）》指出，“原则上，各门课程用不少于10%的课时设计跨学科主题学习”.《义务教育数学课程标准（2022年版）》也指出，在初中阶段综合与实践领域，可“采用项目式学习的方式，以问题解决为导向，整合数学与其他学科的知识和思想方法……提高发现与提出问题、分析与解决问题的能力，发展应用意识、创新意识和实践能力”.

跨学科项目式学习要求以某学科为中心并确定主题，然后运用不同学科或已确定的领域中的观点和思维方式，对该主题展开基础性和实践性的加工和设计.它强化不同学科内容的整合，突出学科思想方法和探究方式的学习，强调知行合一、学思结合，倡导做中学、用中学、创中学.具体到数学学科中，它要求以数学核心素养为中心目标，兼顾创新意识、实践能力、社会担当等综合品质，引导学生对真实情境中的问题进行全面的、理性的思考，进而学会用数学的眼光发现问题、用数学的思维思考问题、用数学的语言表达观点.下面，笔者以“车轮与圆、莱洛三角形”跨学科项目式学习为例具体阐述.

一、跨学科项目式学习的设计与实施

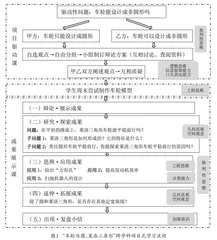
在实践中，笔者基于“数学与工程设计”这一跨学科视角，开展“车轮与圆、莱洛三角形”跨学科项目式学习活动，通过“1+X+1”课时的实践模式，培养学生的创新意识、实践能力、批判性思维、工程思维等综合品质.那么，如何通过项目式学习引导学生探究实际问题呢？笔者尝试先确定项目学习核心，然后通过“创项→入项→研项→出项”四个阶段进行项目设计，实施进阶式学习，以提升学生的综合素养.

（一）定核：聚焦核心素养，发展综合品质

笔者以“车轮能设计成非圆形吗”为驱动性问题，引导学生主动尝试从日常生活、自然现象或科学情境中发现和提出有意义的数学问题，初步学会通过具体的实例，运用归纳和类比发现数学关系与规律，提出数学命题与猜想，并加以验证，勇于探索一些开放性的、非常规的实际问题，从而培养问题意识、发现意识和创造意识［1］.这一过程既可发展学生的空间观念、几何直观、运算、逻辑思维、信息提取、口头表达等多方面能力，也可发展学生的创新意识、实践能力、批判性思维、工程思维等综合品质.

（二）创项：聚焦真实问题，整体联动设计

跨学科项目式学习的实践原型包含组合、递进和冲突三种［2］.“车轮与圆、莱洛三角形”跨学科项目式学习属于递进型，聚焦车轮的形状这一真实问题，引导学生经历“讨论设计→科学制作模型→数学验证模型→工程学应用模型→数学拓展模型→形成出项作品”的学习过程，培养其批判性思维、逻辑思维、信息提取能力、口头表达能力、工程思维、几何直观、空间观念和创新意识.跨学科项目式学习流程如图1所示.

（三）入项：辩论激活思维，自主萌发创新

项目式学习的入项活动需要能够引起学生的兴趣，激发学生的创新欲望，使其想探究、能探究、乐探究，进而吸引全体学生逐渐深入学习.驱动性问题的设计需要把握本质问题，关联学习目标，基于真实情境，联系现实世界，确定展示成果，融入学科实践［3］.

在“车轮与圆、莱洛三角形”跨学科项目式学习中，笔者创设数学思辨环节，以“车轮的形状”为题吸引学生入项，提供两种观点：甲方观点是车轮只能设计成圆形，乙方观点为车轮可以设计成非圆形.活动中，学生独立思考，自主选择观点，持相同观点的学生自行结为一组，并充分、自主地推选组长，防止教师、组长或个别学生的观点替代全体组员的选择.教师则要充分尊重学生的想法，引导每个小组通过讨论交流、网上搜寻资料、图书馆查阅期刊等多种方式，制订讨论方案.在第1课时的驱动课上，笔者引导学生制订方案、辨析方案，进行展评学习.部分学生的观点及阐述如表1所示.

在相互质疑与思辨中，学生的思路被彻底打开，从而较好地培养了批判性思维、逻辑思维、信息提取能力、口头表达能力.

（四）研项：个体创意设计，集体共同研究

1.辩论·展示成果

学生利用周末时间进行探索并尝试制作，然后在课堂上展示成果.甲方小组以PPT和海报形式，展示车轮设计成圆形的优势：一是历史的选择，二是平稳，三是相对节省材料.以下是学生代表对“平稳”的数学解释.

当圆在平坦的路面上滚动时，圆心到地面的距离始终等于圆的半径，其运动轨迹是一条平行于地面的直线.因此，圆形车轮在运动中保持平稳状态.

乙方代表认为车轮可以不是圆形，要根据地面特性确定车轮的形状.以下是乙方的展示.

乙1：如果地面形状是特定的，比如是一条悬链线，根据一定的数量关系，车轮可以设计成正三角形、正方形、正五边形、正六边形等，这样能使得车轮的中心始终与地面的距离保持不变，保证车轮稳定前进.

乙2：如果地面形状是平坦的，是一条直线形，那么车轮形状除了是圆形外，还可以设计成莱洛三角形形状.

设计说明：“车轮能设计成非圆形吗”是一个开放性的、突破常规思维的问题，能引导学生对生活中习以为常的事物进行“求异思考”，提升学生的创新意识与实践意识.

2.研究·探索成果

展示成果时，莱洛三角形形状的车轮可以在平坦的地面上平稳地前行.笔者反问：“虽然模型能够平稳前行，但眼见一定为实吗？”然后提出以下问题，引导学生探究.

问题：在平坦的路面上，莱洛三角形车轮能平稳前行吗？

子问题1：莱洛三角形是如何形成的？它的特征是什么？

子问题2：类比圆形车轮平稳前行，你能探索莱洛三角形车轮平稳前行的原因吗？

【问题探究】

［活动1］探究模型    感知性质

生1：分别以等边△ABC三个顶点为圆心，三条边为半径画圆，三个圆相交部分由三段圆弧围成的封闭图形就是莱洛三角形.莱洛三角形是一个轴对称图形，弧AB长与线段AB长的比值等于[13πAB]∶[AB=π]∶3.

［活动2］模型操作    画板验证

生2：将一块木板放在若干个莱洛三角形模具上滚动，发现木板能平稳前进.通过几何画板验证，发现莱洛三角形在滚动过程中，最高点的运动轨迹是一条平行于地面的直线，但其“中心”的运动轨迹是一条曲线.

［活动3］数学论证    解释说明

生3：图2是莱洛三角形ABC在滚动中的某瞬时状态.记莱洛三角形中心为O，与地面l1的交点为Q，易知☉A与l1相切于点Q，连接AQ，则AQ⊥l1，过点O作OP⊥l1于点P，连接OA，OC.根据莱洛三角形的性质可知AQ=半径=AB=定值，OP=OC·sin∠OCP=[AC3]·sin∠OCP=[AB3]·sin∠OCP=变量（AB为定值，∠OCP为变量）.所以在滚动过程中，莱洛三角形的最高点到地面的距离始终不变，其运动轨迹是一条平行于l1的直线.因此，将木板放在莱洛三角形轮子上，木板也能平稳前进.但莱洛三角形的中心距离地面的高度与sin∠OCP的值相关，随sin∠OCP的值的变化而变化.

设计说明：基于入项辩论和研项的实物展示、动手实践，学生展示了小组的思辨成果，但这些成果缺乏逻辑论证.因此，该环节引导学生运用数学知识对问题“在平坦的路面上，莱洛三角形车轮能平稳前行吗”进行推理论证.在教学中，教师要通过多元支架工具，助力学生的探究与推理证明.在跨学科项目式学习中，成果验证环节是培养学生理性精神和批判性精神的好时机.同时，在数学项目式学习中，不仅要有研究成果的展示，更应引导学生运用数学知识和思想进行分析、评价、阐述和理性思考，培养空间观念、几何直观和推理能力.

3.思辨·应用成果

莱洛三角形是机构运动学创始人莱洛发现的.他发明了300多种机械模型，著有机械工程名著《理论运动学》.莱洛三角形的发现也促进了工程学的进步，例如以下应用.

应用1：钻出“方形孔”（利用莱洛三角形钻出近似方形的孔）

应用2：提高发动机效率（转子发动机中利用莱洛三角形提高发动机的效率）

应用3：扫地机器人的设计

设计部设计了A、B两款扫地机器人，A款是横截面为圆形的扫地机器人，B款是横截面为莱洛三角形的扫地机器人，它们的宽度都是30 cm.

思考1：A款横截面周长是         ，横截面面积是         .

B款横截面周长是         ，横截面面积是         .

思考2：如果你是工厂决策者，你会选择哪款机器人进行量产？为什么？

设计说明：数学是基础学科，可以推进工程设计的进步.这一环节旨在引导学生感受莱洛三角形在工程学的应用，了解应用图形的性质可以解决实际问题，体会数学的有用性，并使其在跨学科的应用中，激发学习与研究的兴趣，今后勇于探索一些开放性的、非常规的实际问题.

4.延伸·拓展成果

问题：除了圆和莱洛三角形，是否存在其他的定宽曲线？

子问题1：在正三角形、正方形、正五边形、正六边形、正七边形、正八边形、正九边形中，是否存在定宽曲线？

子问题2：若存在，请画出定宽曲线.设定宽曲线的宽为d，尝试求周长及面积.你得出了什么结论？

设计说明：数学的创新意识还体现在能够通过具体的实例，运用归纳和类比等方法发现数学关系与规律，提出数学命题与猜想，并加以验证.这一环节是从数学的维度引导学生创新，基于正n边形自主猜想并构造出其余定宽曲线，然后证明，探究n的取值范围.

（五）出项：分层自选作业，具化外显成果

项目式学习的成果分为内隐性和外显性两大类.内隐性成果是学生的核心素养发展和综合品质提升，它需要通过外显的成果来呈现.教师可以通过设计类、展示类、创作类、活动类、策略总结类等类别的表现形式，直观地了解学生的学习进展和收获.如该项目出项时，笔者通过以下四类学生自选的作业，具化外显成果，了解学生的学习进展和素养发展情况：一是撰写数学小论文，学生可以聚焦莱洛三角形的应用与创新点撰写论文；二是绘制数学思维导图，解密“定宽曲线”家族及规律，探索宽度相等的定宽曲线的周长、面积之间的规律等；三是制作车轮模型，展示莱洛三角形车轮的小车如何跑起来；四是发放《莱洛三角形专项练习卷》，待学生上交后，批改其答题情况.在整个跨学科项目式学习中，笔者通过多种评价方法，评估学生的知识获取以及项目进展、成果优劣等.

二、跨学科项目式学习的实施建议

（一）价值导向：打破学科壁垒，培养学生综合品质

在国际比较中，中国学生往往被认为基础扎实，但在创造性、问题解决方面存在不足，这些甚至是“短板”.因此，在当下中国的教育情境中，项目式学习的重要使命之一就是要补齐中国教育的这块“短板”［4］.设计与实施项目式学习时，需要引导学生在真实情境中提升解决实际问题的能力，培养批判性思维、创新意识和工程思维.跨学科项目式学习可突破单一学科壁垒，细化学习目标，兼顾“纵向知识深挖”和“横向知识融通”，促使学生从“掌握学科知识”走向“构建结构化、网络化的认知地图”，有效发挥各学科综合化育人功能，培养学生的综合品质，以及不墨守成规、敢于在继承中创新的精神.