基于表现性评价的数学文化项目式学习设计

摘    要：数学文化项目式学习是在有数学文化味道的项目任务中开展深层次认知活动的教学.教师要结合课程评价的研究，构建基于表现性评价的数学文化项目式学习操作流程，以此促进学生进行自我主导的学习.在项目活动启动阶段，教师要确定主题与表现性目标；在项目任务规划阶段，教师要呈现表现性任务，进行过程性评价；在项目活动开展阶段，教师要引领项目推进，进行过程性评价；在项目作品展示阶段，教师要引导学生展示成果，并评价交流.在设计时，教师要多重关联以确定项目主题，从行为入手以逆向设计表现性目标，提前架构以统领表现性评价实施.

关键词：表现性评价；数学文化；项目式学习

从数学课程的构建到数学学科学习方式的创新再到数学学科学习评价体系的建立，数学教学的各个方面都必须指向数学的深度学习.通过设计深层次认知任务，数学文化项目式学习能够激活学生深层认知思维［1］.而表现性评价关注真实情境中的任务落实，在这个过程中学生进行构建和创造，是撬动深度学习的引擎［2］.二者都是指向学生数学学习深度理解的重要方式.因此，研究基于表现性评价的数学文化项目式学习具有重要意义.

一、基于表现性评价的数学文化项目式学习概述

（一）数学文化项目式学习

张维忠在《数学教育中的数学文化》一书中强调数学文化不仅是人类文化的一部分，还包括数学自身所特有的文化系统［3］.《义务教育数学课程标准（2022年版）》（以下简称“《课程标准》”）指出，课程内容的选择要关注数学文化，继承和弘扬中华优秀传统文化.由此可见数学文化的重要性，但数学文化与数学教育的融合在实际教学中存在程度浅、形式单一的问题.因此，数学文化落地于数学教育需要找到合适的载体，而数学文化项目式学习是数学文化融入数学课堂教学的重要形式.

数学文化项目式学习指教师基于数学文化素材设计具有开放性、操作性的项目任务，指导学生经历发现问题、提出问题、分析问题，融合多学科知识解决问题的过程［4］.在这个过程中，学生是学习的主体，需要变知识接受式学习为问题解决式学习，进而在积极思考与探索中增强创新精神与合作精神.

（二）表现性评价

《课程标准》提出要“创新评价方式方法，注重动手操作、作品展示、口头报告等多种方式综合运用，关注典型行为表现，推进表现性评价”.这给以学生为中心，基于生活情境，指向深度学习的教学与评价指明了方向.表现性评价评的是居于课程核心的目标，而通过学生在真实情境中完成任务时所表现出的创新能力、问题解决能力等，可以检测这些目标的完成度.因更适合检测复杂的思维能力，且更有可能促进这些能力的获得，表现性评价受到当前评价改革的关注.

（三）表现性评价对数学文化项目式学习活动开展的意义

数学文化项目式学习活动是在有数学文化味道的项目任务中开展的深层次认知活动，强调在真实情境中动态发生.传统的纸笔评价方式测定的领域极为狭窄，很难检测基于真实情境解决问题的能力以及完成任务的过程表现［5］，无法反映出学生在整个项目学习过程中的学习状态与水平.表现性评价以其多元化、动态化的特征，成为项目式学习中常用的评价方式［6］.不同于客观测验，它通过学生完成作品、表演等展示出的口头表达能力、书面表达能力、思维能力，对学生的学习过程与成果进行测验，指引学生利用评分规则进行自我引导与反思并改善表现［7］.因此，表现性评价在数学文化项目式学习活动中能发挥重要作用.

二、基于表现性评价的数学文化项目式学习操作流程

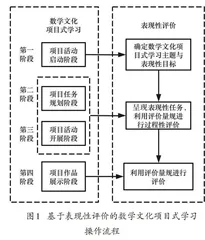
结合课程评价的研究，周文叶构建了表现性评价的概念框架［8］，张辉蓉等人提出STEAM理念下数学文化项目学习模式操作流程［9］.笔者据此构建了基于表现性评价的数学文化项目式学习操作流程（如图1所示）.

表现性评价应贯穿数学文化项目式学习全程，以促进学生进行自我主导的学习.

在项目活动启动阶段，教师需要确定数学文化项目式学习的主题和表现性目标.主题的设计应从文化关联、数学关联、跨学科关联三方面分析［10］.表现性目标的设计应遵循“逆向设计”思路，即在设计前考虑“评价”.一般而言，目标来源于三方面：核心素养目标、高阶思维目标、关键能力目标［11］.确定表现性目标要根据《课程标准》、项目特点、学生发展现状等进行综合考量.

在项目任务规划阶段，教师需要基于上述主题和表现性目标创设真实情境，呈现表现性任务，引发学生的深层次认知活动.在数学文化项目式学习活动中，“任务”贯穿整个学习流程且与表现性目标匹配.

在项目活动开展阶段，教师需要基于表现性任务指导组织活动并管理学生的表现，学生在解决表现性任务中形成作品成果.在此过程中，监控与反馈尤为重要，评价量规是有效开展数学文化项目式学习的评价工具.在每个进阶任务的完成过程中，教师利用评价量规给予学生指引反馈，可以更好地推动项目式学习的进程.

在项目作品展示阶段，学生对学习成果进行汇报和交流.此阶段，师生要围绕学习成果使用评价量规进行评价，对整个数学文化项目式学习活动进行反思.

三、基于表现性评价的数学文化项目式学习案例

（一）项目活动启动：确定主题与表现性目标

从项目开展的时间序列来看，确定项目式学习主题与表现性目标是数学文化项目式学习活动设计的起点.主题设计规定了项目式学习的领域，目标往往是在分析主题的基础上确立的，规定了主题活动的方向.

1.项目主题确定

在数学文化项目式学习主题的确定过程中，教师需要从文化关联、数学关联、跨学科关联三方面进行分析.

其一，从文化关联分析，土圭是中国古代一种测量日影长短的工具，《尚书·尧典》中运用“土圭之法”判别四季，明确耕种时间.《周髀算经》中讲解了周朝如何运用“土圭之法”确定疆域范围，测定“天下之中”.这些都体现了古人的智慧.土圭中蕴含着丰富的数学元素与其他学科知识，在如今的生活中仍具有一定的实用价值，这表明数学是一股重要的文化力量.因此，土圭是一个具有丰富文化价值的素材，由此可开发出一个数学文化项目式学习的主题.

其二，从数学关联分析，在《课程标准》中，“土圭之法”被列入综合与实践活动.以土圭为主题的项目式学习包含“平行线的性质”“解直角三角形”“投影”等丰富的数学知识，能够培养学生几何直观、模型观念、应用意识等核心素养.因此，以土圭为主题可以与数学学习产生紧密的联系.

其三，从跨学科关联分析，利用土圭测量纬度与初中科学学科中的“经纬度”“光的直线传播”有很强的相关性，且学生具有相关知识储备.因此，在数学课程“投影”的学习中以土圭为主题进行项目式学习是可行的.

基于以上三重关联的分析，笔者确立“走进土圭之法，制作节气纬度仪”这一项目主题.

2.表现性目标的确定

设计表现性目标应从学生行为入手，以核心素养为导向，结合关键能力和高阶思维，同时充分彰显文化性.

核心素养目标：会用数学的眼光观察世界，感悟土圭中蕴含的数学知识与文化价值，体会数学与生活的紧密联系，增强民族自信心与自豪感；会用数学的思维思考世界，理解解直角三角形、平行线的性质等数学知识与科学知识的联系，发展几何直观、模型观念等核心素养，探索用土圭测量纬度的方式，并合乎逻辑地设计节气纬度仪的制作方案；会用数学的语言表达世界，用数学和跨学科知识制作节气纬度仪，利用土圭影长表示测量地的纬度，体会数学在现实世界中的价值.

关键能力目标：在理解用土圭测量纬度原理的过程中培养分析解决问题的能力，发展主动思考、质疑反思的能力；在项目活动中培养沟通能力、团队协作能力、规划能力；在制作节气纬度仪的过程中培养设计能力与实践能力，养成热爱动手、勇于创新的良好品质.

高阶思维目标：在考虑实际生活中使用土圭测量纬度会遇到的问题中，培养批判性思维；在设计土圭纬度仪制作方案及制作过程中，培养创造性思维.

（二）项目任务规划：呈现表现性任务，进行过程性评价

在项目式学习活动中，任务是贯穿整个学习流程的线索，既要与表现性目标相匹配，又要考虑评价的合理展开.这样，在完成进阶任务时，学生才既能达成项目式学习的目标，又能清楚评价要点，并在深度评价中促进学习.此阶段以表现性目标为测评导向，以表现性任务为测评范围，要求制订具体的表现标准，并设计评价量规进行过程性评价.

1.创设情境，呈现项目

［情境］在中国古代，运用“土圭之法”不仅测定了四季，还测定了周朝的疆域以及中心.在那个地理知识如此贫乏的年代，人们是如何确定周朝中心的呢？这就要从日影与纬度之间的关系说起.今天，让我们以“走进‘土圭之法’，制作节气纬度仪”为主题开展项目式学习.

［教师活动］播放利用土圭测定四季以及测量距离的视频，让学生了解一年内土圭在太阳光的照射下可以形成长度变化的影子.播放完视频后向学生提问：影子长度的变化和什么有关？什么时候影子长度最短？

预设回答：影子长度和太阳直射点的位置、太阳高度、土圭放置的位置有关.夏至日正午放置在北回归线上的土圭影子长度最短，为0.

设计意图：通过视频介绍及提问，让学生初步了解土圭蕴含的知识以及文化价值，增强民族自信心与自豪感，使学生知晓土圭影子的长度与太阳直射点的位置、太阳高度和放置位置有关，明确研究主题，并为后续学习用土圭测量纬度原理打下基础.

2.任务一：探索利用土圭测量纬度的原理

问题1：根据生活经验和科学知识，正午时日影方位与什么因素有关？

设计意图：让学生思考某地正午日影方位与该地的纬度和太阳直射点的位置有关，为后续制作节气纬度仪作准备.

讨论某地正午日影方位，可以将问题抽象成图2.假设此时太阳直射点为A，位于A北面的B处正午日影方位为正北，位于A南面的C处正午日影方位为正南.

问题2：假设时间为夏至日正午，如何根据日影计算土圭放置点的纬度？

设计意图：引导学生利用“解直角三角形”“平行线的性质”“投影”等数学知识和“经纬度”“光沿直线传播”等科学知识，根据夏至日正午影子的长度与方位计算纬度，明晰土圭测量纬度的原理，调动学生思考的积极性.

计算夏至日正午时土圭放置点的纬度，需要将实际问题抽象化、数学化.如图3所示，计算[A]处的纬度，此时太阳直射北回归线，正午时北回归线（[B]处）日影长度为0.因为太阳距离地球很远，可以假设照射在[A]处和[B]处的光线是平行的.不妨设北回归线的纬度为α，[A]处的日射角为β，[A]处的影长为[x]，土圭高为[h]，有[tanβ=xh]，可以利用计算器算出β的值.因为内错角相等，所以地心角[∠AOB=β]，那么[A]处的纬度就是[α+β].这就是说，夏至日正午在北回归线以北处，测量地的纬度就是日射角加上北回归线的纬度.同理，夏至日正午在北回归线以南至赤道之间的测量地的纬度就是北回归线的纬度减去日射角，而赤道以南测量地的纬度就是日射角减去北回归线的纬度.

3.任务二：厘清用土圭测量纬度需要考虑的实际问题

问题3：根据上述原理，能否制作一个纬度仪？在制作过程中需要考虑到什么实际问题？

预设回答：上述原理仅介绍夏至日正午的日影与纬度的关系，限制了土圭的使用时间，缺少实用价值；在测量时，太阳光是必不可少的，而在阴天无法使用，这局限了土圭的使用范围；为增加精度，必须使用更长的土圭，携带上存在不便.

设计意图：任务二将理想情况引向现实生活，引导学生考虑实际情况，培养学生会用数学的眼光观察世界，会用数学的思维思考世界，发展其批判性思维和理性精神.

学生发现了使用土圭测量纬度时存在的问题，其中一些问题易于解决.如中国古人早已知道不同节气太阳直射点的纬度，甚至一年内不同时间太阳直射点的纬度，那么土圭的使用时间就不局限于夏至日；又如可以使用轻便可折叠的材料制作立杆，解决携带不便的问题.但土圭必须在有太阳光的时候使用这一缺陷无法消除.教师可引导学生在课后了解用现代仪器测量纬度的方式，感受技术的飞跃发展.