“思想共生、素养共长、文化共育”数学教学探究

摘    要：为解决当前数学教学中“重知识、轻素养、缺文化”的现象，教师有必要创设“思想共生、素养共长、文化共育”课堂.教师可分析教材相关内容所蕴含的数学思想、数学素养、数学文化，根据中国学生发展核心素养与数学学科核心素养的培育要求，有机融入本土文化，对教学进行设计.具体实践中，教师可从“创设情境，疑点反思”“尝试解疑，问题反思”“问题解决，应用反思”“课堂练习，方法反思”“课堂总结，提升反思”“布置作业，梳理反思”六个环节实施教学，一步步引导学生实现“思想共生、素养共长、文化共育”.

关键词：思想共生；素养共长；文化共育；初中数学教学

《义务教育数学课程标准（2022年版）》（以下简称“《课程标准》”）明确了核心素养的内涵及主要表现，提出要让学生“获得适应未来生活和进一步发展所必需的数学基础知识、基本技能、基本思想、基本活动经验”，要求“关注数学学科发展前沿与数学文化，继承和弘扬中华优秀传统文化”.然而，当前数学课堂教学中“重知识、轻素养、缺文化”的现象仍然普遍存在，这是因为一线教师并未足够重视对学生进行“思想的渗透、素养的培育、文化的浸润”.基于此，笔者以参加山东省“黄河文化育人资源的整合与运用”现场会为契机，设计并展示了“认识二元一次方程组”一课，旨在落实《课程标准》提出的新理念，实现“思想共生、素养共长、文化共育”，下面详细介绍.

一、“思想共生、素养共长、文化共育”下的内容及教学解析

（一）内容解析

“认识二元一次方程组”是北师大版义务教育教科书《数学》八年级上册第五章的内容，是该章起始课，旨在引导学生感受二元一次方程（组）学习的必要性，及其在解决问题中的优越性等.二元一次方程组是一类最简单的线性方程组，它是刻画现实世界数量关系的一个有效数学模型，也是学习数学乃至物理、化学等其他学科知识的重要基础.“认识二元一次方程组”一课既是一元一次方程的延续，又是进一步学习其他方程的前提，与研究一元一次方程的“基本套路（定义、解法、应用）”相同.该课蕴含丰富的数学思想、数学素养、数学文化.

数学思想：方程是刻画现实世界数量关系的有效模型、类比思想、建模思想.

数学素养：模型观念、运算能力、应用意识.

数学文化：该章“章前图”为学生呈现了古老的数学问题——鸡兔同笼；该章第1、2个情境分别以图文并茂的形式为学生呈现了《希腊文选》中记录的“欧几里得问题”及现实生活中的“购票问题”.

此外，该章引言为学生提供了内容学习的路径和方法，该章第2个情境还意在引出“二元一次方程（组）解”的概念，教师应对其有足够的重视.

立足上述分析，为体现单元整体设计和学科育人理念，笔者结合本地实际情况，创设“‘保护湿地生态  传承黄河文化’主题研学旅行”大情境，在保证实现该章第1、2个情境目的的基础上，着重引导学生于欣赏家乡美的同时，领略黄河文化的魅力，感受环境保护的必要性，并确定这节课的教学重点：了解二元一次方程（组）的概念及其解的意义.

（二）教学目标及解析

《课程标准》对这节课的要求是：能根据现实情境理解（二元一次）方程的意义，能针对具体问题列出（二元一次）方程；理解（二元一次）方程解的意义.由此，笔者设计这节课的教学目标并作解析.

1.教学目标

目标1：在具有文化意味的情境问题的解决中，再次感受（二元一次）方程是刻画现实世界数量关系的有效模型.

目标2：在具有文化意味的情境问题的解决中，概括二元一次方程（组）的概念；体会二元一次方程（组）解的意义.

目标3：在具有文化意味的研学过程和课堂学习中，培养保护环境和自强爱国的个人情怀，培育模型观念、运算能力、应用意识等核心素养.

2.目标解析

目标1达成的标志是：学生能在具体情境中发现两组等量关系，并在灵活设置未知数的基础上，准确列出方程.

目标2达成的标志是：学生能通过相应的探究活动说出二元一次方程（组）的概念；学生能说出二元一次方程（组）解的概念，并能判断出一组数是不是某个二元一次方程组的解.

目标3达成的标志是：学生能感受到“数学来源于生活，又服务于生活”，体会到二元一次方程（组）学习的必要性，及其在解决问题中的优越性；学生能在具体情境和问题解决中种下“保护环境”和“自强爱国”的种子，逐渐成长为“有理想、有本领、有担当”的“三有”时代新人.此目标属于情感、态度与价值观方面的目标，需要在长期过程中慢慢形成.

（三）教学问题解析

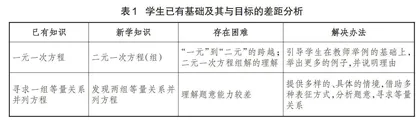
通过一元一次方程相关内容的学习，学生基本具备了在具体情境中寻求一组等量关系的能力，能够用一元一次方程解决现实生活中的实际问题，具备了学习新方程的能力和条件，但学生对“元”和“次”的认识，仅限于“一元”“一次”的感性认识，且难以利用方程表示相对复杂的等量关系.学生已有基础及其与目标的差距分析如表1所示.

通过上述分析，笔者确定这节课的教学难点：在具体情境中，发现（两组）等量关系，列出二元一次方程（组）.

二、“思想共生、素养共长、文化共育”数学教学设计说明

（一）思想共生

《课程标准》要求培养学生的数学基础知识、基本技能、基本思想和基本活动经验，而由于思想具有再生性，教学中对基本思想的渗透至关重要.

教师可先引导学生在回顾一元一次方程知识的基础上，通过类比思想，帮助学生自主建构二元一次方程（组）的基础知识（定义及其解的概念），然后在小结中为其他方程的学习进行“预设”，以充分体现类比思想的重要作用.教师应将建模思想贯穿教学始终，化解学生后续在“应用”学习中的压力，以实现类比思想和建模思想等不同数学思想的共生.

（二）素养共长

在中国学生发展核心素养方面：先引导学生欣赏诸如“山东黄河三角洲国家级自然保护区”的宣传片，感受环境保护的必要性，培养“责任担当”素养；再引导学生通过类比的方法，自行归纳二元一次方程（组）的定义及其解的概念，积极践行“学会学习”素养的培育；最后，设计多个反思环节，引导学生及时进行梳理总结，将新知纳入原有知识体系，争做“勤于反思”的好学生.

在数学学科核心素养方面：先引导学生用数学的眼光观察现实世界，在相关情境中提出数学问题；再引导学生用数学的思维思考现实世界，并提供类比这一思维支架，使其展开自主思考和探究；最后引导学生用数学的语言表达现实世界，用自己的语言自行归纳并获得二元一次方程（组）的定义及其解的概念.

教师要通过相关问题的解决和情境的分析，培育学生模型观念、应用意识等核心素养，为落实《课程标准》的总体目标和要求进行积极的探索和实践，实现中国学生发展核心素养和数学学科核心素养的共长，或学生数学学科各核心素养的共长.

（三）文化共育

中华文明源远流长，孕育了中华民族的优秀精神品格，培育了中国人民的崇高价值追求，在课堂教学中具有很好的育人价值.2021年2月，《中华优秀传统文化进中小学课程教材指南》正式颁布，标志着传统文化进课堂势在必行.

为更好地发挥数学学科的育人价值，教师要充分挖掘地域文化，如可通过“‘保护湿地生态  传承黄河文化’主题研学旅行”这一大情境，引导学生在知识掌握的同时，感受黄河文化中所蕴含的“家国天下、自强不息、崇德尚义、乐知天命、兼收并蓄”等内涵精髓.教师应充分发挥数学学科本身所具有的理性精神，在问题探究和解决中，培养学生严谨的数学思维和坚毅的数学品格.此外，教师还要融入部分数学文化类题目（欧几里得问题、鸡兔同笼问题等），使学生在耳濡目染中提升文化认同和文化自信，实现数学文化和黄河文化的共育.

三、“思想共生、素养共长、文化共育”数学教学设计案例

笔者以“思想共生、素养共长、文化共育”为视角，尝试对“认识二元一次方程组”进行教学设计.

（一）创设情境，疑点反思

笔者播放“山东黄河三角洲国家级自然保护区”的宣传片，创设“‘保护湿地生态  传承黄河文化’主题研学旅行”大情境，并将之细化为若干小情境，引导学生感受家乡美，学会用数学的眼光观察现实世界，并从中发现或提出数学问题.

［情境1］已知某研学小组师生共6人，买门票花费240元（成人门票60元，学生半价），根据这些情况，你能提出哪些数学问题？

［预设］教师和学生分别有多少人？用一元一次方程解决（设一个未知数），但有部分学生可能会设两个未知数.

［情境2］同学们乘坐景区内游船，体验“黄蓝交汇”的旷世奇观.1艘东方白鹳号游船可乘坐16人，1艘丹顶鹤号游船可乘坐22人.丹顶鹤号游船数的一半比东方白鹳号游船数的2倍少1，两种游船共载164人，每艘游船没有空位.根据这些情况，你能提出什么数学问题？

［预设］各有多少艘游船？尝试用一元一次方程解决，但是对部分学生来说存在一定困难；进而设两个未知数，抽象等量关系，列出方程.

［师生活动］通过教师引导和学生自主探究，学生在情境1和情境2中抽象出等量关系，然后列出方程.情境1可用“设一个未知数或两个未知数”的方法轻松得到方程；情境2在用“设一个未知数”解决时可能会存在一定的困难，所以教师可引导学生“设两个未知数”，通过等量关系列出方程.

设计说明：以有关联的两组情境，引导学生由易到难，在逐步应用类比思想解决问题的过程中，去体会建模思想，为实现“思想共生”奠定基础.通过“‘保护湿地生态  传承黄河文化’主题研学旅行”这一大情境，引导学生在“购票”和“乘坐游船”等实际问题中，发现或提出数学问题，让学生用数学的眼光观察现实世界，培育学生的数学学科核心素养，同时引导学生在感受“黄河之水天上来，奔流到海不复回”的壮观和欣赏“山东黄河三角洲国家级自然保护区”美景的过程中，感受家乡的美丽富饶、祖国的繁荣昌盛，培养“爱祖国爱家乡”的家国情怀，实现中国学生发展核心素养的培育，由此为实现“素养共长”奠定基础.该环节还渗透黄河文化，为后续实现“文化共育”奠定坚实的基础.

（二）尝试解疑，问题反思

［任务1］复习一元一次方程，了解其定义、解法、应用.

［预设及师生活动］教师搭建脚手架，引导学生回忆“元”和“次”的概念.在情境1的基础上，学生回忆一元一次方程学习的“基本套路”，并在“问”和“追问”中重建已有知识体系，明晰“元”和“次”的概念.随后，教师出示这节课的教学目标.

设计说明：回忆一元一次方程中“元”和“次”的概念，引导学生利用类比思想，为后续顺利建构二元一次方程（组）的概念作铺垫，体现“思想共生”.学生在重建知识体系的过程中，可加强会用数学的思维思考现实世界的能力，并能为后续会用数学的语言表达二元一次方程（组）及其解的概念奠定基础，体现“素养共长”.此外，出示教学目标，渗透这节课及整章的研究思路和方法，能体现知识的系统性和一致性.

（三）问题解决，应用反思

【任务2】二元一次方程的定义.

观察思考：以上几个方程具有哪些共同特征？

［预设及师生活动］在类比一元一次方程定义的基础上，学生可以轻松地用自己的语言给出二元一次方程的定义；教师以“追问”引导学生进行完善，进而获得准确的定义.

设计说明：引导学生在类比的基础上，自行归纳获得二元一次方程的定义，体现“思想共生”.

［任务3］二元一次方程组的定义.

问题1：在情境1中得到的两个方程中，x所代表的对象相同吗？y呢？