混合式教学下高等数学课程思政建设的优化路径

摘  要：课程思政理念融入大学数学教育，对培养合格的社会主义接班人起到重要作用。基于大学边界理论的视角，在CSCL为基础的协助学习环境中优化高等数学课程与思政课程之间的边界。在具体的课堂教学情境中，将知识学习、价值凸显与能力培养进行有机结合。在大学数学类课堂教学中强调辨析社会系统中的数学、复杂性问题解决、工程伦理以及数学价值观的塑造。

关键词：混合式学习；CSCL情境；高等数学；价值澄清法；规范伦理

中图分类号：G641        文献标志码：A          文章编号：2096-000X（2024）04-0165-04

Abstract： The integration of ideological and political concepts into college mathematics education plays an important role in cultivating qualified socialist successors. Based on the perspective of university boundary theory， the boundary between higher mathematics courses and ideological and political courses is optimized in the assisted learning environment based on CSCL. In the specific classroom teaching situation， knowledge learning， value highlighting and ability training are organically combined. In the classroom teaching of College Mathematics， it is emphasized to differentiate and analyze mathematics in the social system， complex problem solving， engineering ethics and the shaping of mathematical values.

Keywords： blended learning; CSCL situation; higher mathematics; values clarification method; regulating ethics

2018年9月全国教育大会和2019年3月学校思想政治理论课教师座谈会上，习近平总书记着力强调“课程思政”的重要性和迫切性。国家教育部在精品在线开放课程和金课建设的评审过程中，对课程思政也明确提出要求：统筹标准、课程、教材、教学、评价与考核等各环节，加强课程思政教师队伍建设，构建“思政课程+课程思政”的育人大格局。2020年6月教育部又进一步印发《高等学校课程思政建设指导纲要》，强调把思想政治教育贯穿人才培养体系，力争实现思政课程与课程思政的同向同行。

一  大学数学课程思政与思政课程建设的同向同行机制

（一）  大学边界理论

边界优化理论是实现二者同向同行、优化立德树人共同体运行机制的基本原理，主要包括科学设置边界、维持稳定边界、促进边界渗透、合理跨越边界、优化运行机制和科学管理边界等环节[1]。课程思政是以课程为载体，通过挖掘课程知识本身的思政元素，以隐性的方式实现对学生实现价值的引领。思政课程是透过特定教育内容的学习对学生展开马克思主义教育的课程形式。二者的有机结合与同向同行，旨在着力形成课程群对学生立德树人教育的学科合力。作为性质与定位都不同的课程，正确认识与把握它们的边界有助于更好地发挥它们的协同作用。在具体的教育场景中，如何把握好二者的边界实现课程内容的渗透和跨界是一项挑战性任务。通过挖掘大学数学课程的思政元素和其所承载的教育功能，在价值澄清中能逐步实现课程思政与思政课程的边界优化。

（二）  CSCL学习情境

如何把理工科核心课程的课程思政建设做好做优是亟待解决的问题。信息技术与学习科学相互作用，体现出错综复杂的关系。在资讯科技结合与支持学习的方式中，混合式教学将面对面学习与网络活动结合在一起，为技术与教学的深度融合创生出良好的外部环境[2-3]。混合学习模式下学习成果评量架构，以科学素养、核心能力为主轴，以正式课程、非正式课程为依托，相互验证能力学习成果。能力学习成果的下位概念有课程学习成果和单元学习成果。针对不同形式的作业分别制定出不同的评量标准，这些标准引导着学生深度学习，也协助教师进行客观的评估活动。

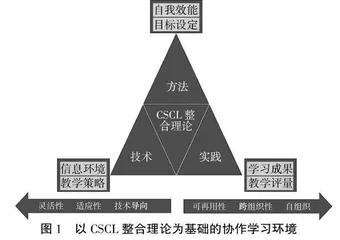
有三个早期的研究项目是CSCL作为一个研究领域形成的先驱。这三个项目分别是：加拉德特大学的ENFI，多伦多大学的CSILE以及加州大学圣地亚戈的第五维项目。它们都探索了如何用科技来帮助学生学习读写。这三个研究项目的共同目标，都是通过信息技术赋予教学更多的意义。它们是一个理想的计算机支持下的协作学习（Computer-Supported Collaborative Learning，CSCL）系统，需要具备高度抽象的特性。其运用符合学习者思考模式的方式设计与开发系统，以降低教师和学生使用上的技术门槛。其提供出教师线上课程的管理、线上课程问卷的编辑及同伴间线上资源共享空间（图1）。CSCL的研究方法主要有观察描述、实验法与循环设计三类。在数学科学里，不断激发学生在小组学习中体认到其科学文化价值、应用价值和审美价值的做法日益得到重视。融合计算机支持与协作学习来有效地促进学习正是CSCL学习情境所面对的挑战。混合式教学模式下大学数学课程的思政建设，旨在发挥计算机辅助协作学习的优势，不断优化数学课程与思政课程二者之间的边界[4-5]。

二  大学数学课程思政的逻辑起点

（一）  价值澄清教学法

价值澄清教学法最早由瑞斯（L.E. Raths， 1966）和西蒙（S.B.Simon，1972）提出，旨在协助学生了解并确定出自己或他人的价值。与传统的传授特定的观念不同，价值澄清教学法更强调价值的形成过程，重视个人选择价值的本领。瑞斯等认为只有澄清出个人或事物的价值，主体才会朝向特定目的做出合理的思考判断。价值澄清教学法的教学过程，可分成了解、关联、评价与反省四个时期。在学校教育中施行价值澄清教学法，要结合学生的个人背景、性格和能力等因素，而不是按照固定的流程开展。

在大学数学课堂教学中实践课程思政教育，不能只片面强调学生能识别和辨析社会系统中的数学、解决复杂问题时能熟练运用数学，更重要的是要在课堂教学中开展数学价值塑造。课堂教学文化冲突的根源在于，师与生在价值观念、信息资源与符号表征等方面都有相当大的差异。教育主体按自身的文化属性去表达，课堂上师生在文化冲突中逐步实现视域的融合。在能力培养与知识传递的同时，学生构筑起对数学学习的信心，进而把数学当作为一种文化要素进行鉴赏。数学作为一种定义良好的话语并不意味着只存在单一的数学话语。不同的社会、文化和历史存在不同的数学话语实践[6]。数学的真善美是数学表现力的主要侧面。数学知识都是以真理性为依归，善是衡量数学功用价值的关键尺度，美是其艺术价值的体现。以真、善、美为重要表现力，可建构出数学课程思政教育的有效路径。

（二）  混合式教学下的高等数学学习

传统的高等数学教材逆历史发展顺序进行编排，从自实数系统出发以？着-？啄语言的逻辑表述为开端。大部分高校教师认为，只有抽象性数学语言才能揭示概念间的逻辑关系。他们只重视知识的传递，忽略了对学生进行价值引导。数学思政课程建设是价值导引和价值创造的过程。正如习近平总书记强调的那样：“办好思想政治理论课关键在教师，关键在发挥教师的积极性、主动性、创造性……要给学生心灵埋下真善美的种子”。依托真、善、美三个主要维度培养学生对数学学习的美好情感和态度，积极形成良好的数学教学生态是建设大学数学思政课程的有效路径。具体来看，需要从以下四个方面做出努力。

1  明确高等数学课程思政的标准与评价方式

高等数学作为大学数学公共基础课，既是理工科大学生的专业教育课，又属于通识理论课。理工科大学数学课程中的思政教育不是表面的全面化，也不是概论式的肤浅式教育。只有对散置在不同领域中的点做深度学习，才能促进学生本身将知识点连接成线或面。大学生对数学知识的专业需求，需要更深层次的价值关联型文化脉络性知识。需要对散置在不同学科领域中的知识群进行重组与优化。以正式课程和非正式课程为依托，通过科学素养、文化素养和核心能力验证学习成果。评价层次主要有背景评价、输入评价、过程评价与成果评价四个维度。不同的评量标准适用于不同的学习阶段，从而逐步引导学生进行深度学习。

2  案例设计为本的高等数学课堂教学实践

针对极限、连续、导数、投影、幂级数和微分方程等核心知识点群，从文化与应用价值层面进行教学设计。以“逆向设计，正向实施”的课堂教学设计协助学生理解核心知识的具体应用与伦理规范。透过重构课堂教学设计和适时的教学介入，来考察学生的课堂学习实践。面对高等数学课程的基础性和通识性，从课堂内与外侧重辩证唯物主义进行案例开发。积极做好大学生的思想引领、价值引领与伦理规范，推进立德树人融入大学数学教育。像极限概念就是本科生学习微积分的基础概念，历史上刘徽与阿基米德对求圆的面积都曾做出重要的探索和成就。但是，二人的处理方法和思路并不相同。当刘徽遇到阿基米德，思维的火花碰撞激发出东西方数学思维的不同。在文化的脉络中，可以看出刘徽多次运用极限的思想处理问题。该学科案例的科学文化价值可以增强学生数学课程的学习信心与文化自信。

3  价值教学凸显的高等数学课程思政教育

从理性层面看，数学理性是通达善的工具和关键途径；从价值层面看，数学和善的关系转化为模式和价值的关系；从社会层面看，数学知识指向人与人、人与社会的关系；从伦理层面看，数学规范和他者伦理是其本源性动力与内在意义[7-8]。在数学价值教育中，使学生逐步体认到数学兼具“工具”和“文化”两种品格。明确数学应用的精确性与广泛性的同时，不断培育学生的数学文化素养。

像“无穷小与无穷大”的思政课程设计中，首先，可以通过可视化的Koch雪花与Sierpinski船帆的直觉冲击，产生学习者的认知冲突。其次，如何正确地理解无穷小量成为师生面对的共同课题。无穷小量与很小的数什么关系，牛顿在物理问题的解决过程中如何处理无穷小，无穷小与函数极限的关系是什么，这些问题在共同体的探究中交织着出现，一一得到澄清和解决。最后，在价值澄清的教学过程中，学生逐步达成对无穷小量的概念性理解。在科学史上，开普勒也多次运用无穷小论证法来求面积与体积。可以通过“求圆的面积、求球的体积以及求葡萄酒桶的体积”三个教学例题的展示，说明开普勒运用无穷小量处理问题时的原子论精神和实质。我们要强调历史情境中的高等数学学习，透过学科德育使学生成为积极、关怀和反省的学习者。

在数学通识教育中发挥课程思政的功能，让学生透过对数学的整体性了解，增强文化自信并激发自身学习力。让学生感受数学多元价值的同时，发展数学欣赏与理性反思的能力。透过大学数学文化素养的培育，有效通达实践课程思政教育的目标。确立课堂环境、师生角色、价值实践、社会数学规范与学业成就五个维度，促使大学数学思政课程成为一个自组织系统。理性、价值、社会和伦理四个维度相互关联和依存，成为一个自校正、自指导和自组织的复杂系统（图2）。

4  建构思政课程与高等数学课程思政的“课程共同体”