过程控制工程课程混合式教学中学生学习风格模型的构建及应用实践

摘  要：大学生线上线下混合式教学中存在问题产生原因之一是缺乏对网络环境下学生行为数据的分析，从而无法判断学生的学习风格。因而基于数据挖掘技术，利用网络学习平台收集过程控制工程课程学习行为数据，建立基于灰狼算法优化支持向量机构建多维度的学习风格模型，处理和预测其可能的学习风格。有助于教师及时掌握学生动态，调整线上线下混合式教学方案，实现因材施教的个性化教学模式。

关键词：学习风格；灰狼算法；模型预测；学习行为；个性化教学

中图分类号：G640        文献标志码：A          文章编号：2096-000X（2024）05-0049-05

Abstract： One of the reasons for the problems in the online and offline hybrid teaching of college students is the lack of analysis of students' behavior data in the network environment， so it is impossible to judge students' learning style. Based on the data mining technology， this paper collects the learning behavior data of Process Control Engineering course by using the network learning platform， establishes a multi-dimensional learning style model based on the Grey Wolf algorithm optimization support vector mechanism， and processes and predicts its possible learning styles. This research is helpful for teachers to grasp the students' trends in time， adjust the mixed teaching scheme of online and offline， and realize the individualized teaching mode of individualized teaching.

Keywords： learning style; Grey Wolf algorithm; model prediction; learning behavior; individualized teaching

近年突如其来的新冠感染疫情，导致大学生只能转为网络在线学习。虽然高校实现停课不停学，但是在全新的网络授课模式下，教师与学生在空间上是分离的，教师缺乏有效的手段去掌握学生学习过程和学习动态。这就导致部分学生学习效果不佳、成绩下降。出现了诸如学生时间管理不合理，效率低；在巨量的网络资源面前，学生不知从何学起；学习过程中持续动力不足，易放弃，学习兴趣不浓等问题。分析其原因，其中很重要的一条就是缺乏对学生学习行为数据的深入分析。所以在网络教学中若要实现根据学生学习行为特点授课，就需要思考采用什么方法通过学生们的学习行为数据推断学生们的具体学习风格。如今，在后疫情时代，网络授课并没有停止，而是更广泛地应用于线上线下混合式教学。因而对网络教学中学生学习风格的研究也有着重要意义。

早在2005年，马来西亚的国际伊斯兰大学就开展了对学习管理系统的研究[1]。2006年，国内研究者彭文辉等[2]给出了一个基于网络学习行为分析的学习平台结构，但没有用数据验证其有效性。2012年，魏顺平[3]根据网络日志，探索在线学习行为的影响因素。但并没有对学生的学习风格进行划分。

目前，对于学习风格的研究，大多采用的方法有两个：协作，用问卷调查获得的数据建立模型判断学习风格，但问卷带有主观性，不能反映出学生的真实风格；自动识别，通过对学习行为数据的自动采集，利用一定的计算规则，大多采用机器学习算法计算其学习风格，比如贝叶斯网络、神经网络等，但在数据的获取方面存在一定的困难[4]。

支持向量机（Support Vector Machines，SVM）的出现，在处理小样本以及非线性数据问题上，提供了良好的建模性能，进而使预测结果也更加准确。但其参数设置会对预测结果有较大影响，因而考虑优化SVM网络参数。灰狼算法（Grey Wolf Optimization，GWO）具有良好的自组织学习性，而且参数简单、全局搜索能力强、收敛速度快、易于实现[5]。综上所述，可以使用GWO对SVM进行优化，建立学习风格预测模型。

综上所述，基于GWO-SVM算法，利用线上学习综合平台采集学习者的网络学习行为数据，从多个维度构建大学生的在线学习风格模型，利用此预测模型对大学生的学习风格进行划分，实现因材施教，进而达到针对性教育教学方式。对于学生自身，能帮助其发现潜在的学习风格，对于教师，能帮助其了解教学动态，以便动态调整教学方案，实现因材施教的个性化教学，也可为大规模、个性化和高质量的下一代智能学习平台提供技术支撑。

一  学习风格

1954年，学习风格（Learning Style）这个概念是由美国学者哈伯特·塞伦扭首次提出的，而学习风格一度被称为“现代教学的真正基础”。但国内外研究者们并没有给学习风格一个确切的定义。Kinsella认为“学习风格是指个体长期坚持的一种偏爱方式，该方式是学习者在处理和分析获取的知识的进程中所表现出来的惯有的方式”[2]。

最近，国内研究者们引用较多的是谭顶良教授给学习风格下的定义，谭教授[6]认为“学习风格是个体学习者所表现出的持续性的学习方式，囊括了学习者的在学习过程中的策略和倾向，展现出了学习者鲜明的个性”。将上述研究者们的观点进行综述，发现他们普遍都认为学习风格是学习者相对稳定的学习方式，该学习方式能够通过一定的学习行为进行展现。

（一）  学习风格的分类

目前，比较有代表性的学习风格划分模型有如下几种[7]。

1  Kolb模型

Kolb模型是将学习风格置于学习者的学习过程中，同时依据学习风格的知觉及加工动力特性将学习风格划分为聚合型、同化型、发散型、顺应型四种类型[8]。

2  Lotas模型

研究者Lotas依据学习者心理的类型，将学习风格划分为情感Ⅰ、情感Ⅱ、认知Ⅰ、认知Ⅱ四种类型[2]。

3  Felder-Silveman模型（简称FSLSM）

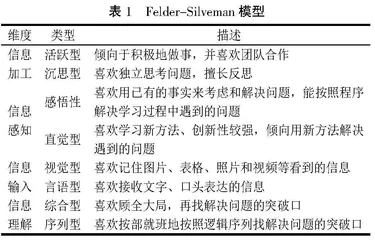
FSLSM是由国外研究者Felder和Soloman在1997年研发的，也是目前为止使用为广泛的学习风格模型，该模型的主要研究内容有自适应的用户建模、分析学习风格、推荐学习策略等，见表1[9]。

FSLSM拥有较强的信度与效度，而被相当多的研究人员所接受，其稳定实用的教育教学效果也被众多研究人员所证实，特别适用于线上教学，因此，本文选择FSLSM。

（二）  学习风格类型与网络学习行为的匹配

1  信息加工维度

活跃型，较多地利用网络教学资源协助教学，倾向于学习者之间的交流。倾向在论坛中讨论、回答问题，发帖数很大，论坛访问时间很长，经常参加课堂互动。

沉思型，倾向独自解决问题，学习者在做出下意识行为之前更倾向独立认真思考。在论坛中阅贴数很大，很少回帖；擅于独立认真思考每个问题，认为没有错误后再提交正确答案，因此，提交答案的时间很长。

2  信息感知维度

感悟型，喜欢事实和具体的学习材料，比较细心。在交作业前认真检查，提交时间更长。倾向于用更多的文字来表达，通过在讨论区发帖、回帖等行为来解决问题。

直觉型，思维更加灵活创新一些。学习者更注重抽象事物，线上访问量大、时间充足，但是完成课堂预定内容数较少。

3  信息输入维度

视觉型，学习者擅长浏览网络图片、表格、视频等网络学习资源的时间充足、频率较多。

言语型，学习者擅长阅读以文本为主的学习资源，任务点完成率高。发帖、看帖多。

4  信息理解维度

综合型，倾向于全局思考，访问教学大纲、知识点总结的次数多、时间长。学习天数多。

序列型，倾向于按照序列进行学习，点击上一页、下一页导航按钮的次数多。

二  GWO-SVM模型

（一）  SVM原理

由国外研究者Vapnik等提出了支持向量机（SVM）的概念，SVM的出现，在处理小样本以及非线性数据问题上，提供了良好的建模性能，进而使预测结果也更加准确[10]。

SVM可以将小样本以及非线性数据问题归纳为一个寻优问题。

假设训练样本集为

式中：n表示样本数，xi是第i个样本，yi∈{-1，1}。

SVM的寻优问题可转化为下述约束优化问题

式中：ω表示求解的最优超平面的法向量；b表示偏移量，ωx+b=0即为所寻找的最优超平面。

假设训练样本线性不可分，为求出最优超平面，核函数k（xi，xj）必须满足Mercer条件，即

k（xi，xj）=Φ（xi）·Φ（xj） 。 （2）

依据前文所述，选择合适的核函数k（xi，xj），可实现非线性训练样本的线性分类。继续引入松弛变量ξi后，分类面表达式可描述为

式中：ω表示分类面的权系数向量；b表示分类的域值。因此，可将寻优问题转化为

式中：c表示惩罚因子。

通过引入拉格朗日乘法算子之后，将核函数内积引入表达式（3）可以得到如下表达式

综上所述，可以得到最优分类面表达式

（二）  灰狼优化算法

1  灰狼优化算法概述

2014年，学者Mirjalili提出了灰狼优化算法，模拟狼群家族的社会制度和狩猎策略，利用迭代的方式不断寻优的群优化算法。灰狼优化算法，具有结构简单、收敛速度快等优点。

狼以群居为主，每个狼群中平均有7～12只狼，具有较为严格的等级制度[11]。按社会地位高低依次定义α、β、δ、ω狼，α为头狼，β是α的顾问，δ听从α和β的指示，ω负责跟踪围捕猎物。

2  灰狼优化算法数学模型

D为狼群与猎物的距离，其数学模型用公式（7）表示，狼群会根据猎物位置和D更新其位置，如式（8）所示

式中：X表示狼的位置向量；Xp表示猎物的位置向量；t表示当前迭代步；A、C表示可调整系数向量，使狼群迅速到达猎物周围的不同位置，根据式（9）和（10）计算

式中：在迭代过程中，a从2到0线性减小；r1和r2表示[0，1]之间的随机向量。

首先，确定头狼α，顾问β和δ到猎物的距离，由公式（11）所示，再根据公式（12），ω根据这3头位置最优的狼来更新自己位置。通过以上算法，即可得到最优解

（三）  GWO-SVM模型构建

在SVM模型中，参数有着非常重要的作用，人为给定参数值会导致预测结果不理想，所以，优化参数是非常有必要的。利用灰狼算法优化SVM中的惩罚因子c和核参数σ这两个参数，可以有效地提高SVM模型预测的准确率。