智慧教学模式赋能概率论与数理统计教学改革

摘  要：在“互联网+”背景下，一些学者将MOOC融合SPOC进行翻转课堂和混合教学以提升教学质量。为充分发挥MOOC+SPOC的优势，培养新时代大学生应具备的数学能力，结合概率论与数理统计课程培养方案，提出基于MOOC+SPOC+雨课堂直播的融合式智慧教学模式。以“中心极限定理”知识单元为例介绍融合式智慧教学模式下具体教学设计和实施过程。结果表明，雨课堂直播教学与MOOC+SPOC融合的智慧教学模式提高学生学习兴趣，体现以学生为中心的教学思想。

关键词：智慧教学；MOOC；SPOC；雨课堂；概率论与数理统计

中图分类号：G642        文献标志码：A          文章编号：2096-000X（2024）15-0038-04

Abstract： Under the framework of "Internet plus"， some scholars integrate MOOC with SPOC to conduct flipped classroom and blended teaching to improve teaching quality. In order to fully leverage the advantages of MOOC+SPOC and cultivate the mathematical abilities possessed by college students in the new era. According to the curriculum scheme of Probability Theory and Mathematical Statistics， a blended intelligent teaching model based on MOOC+SPOC+rain classroom live streaming is proposed. Taking the "Central Limit Theorem" knowledge unit as an example， the specific teaching design and implementation process under the blended intelligent teaching model are introduced. The results indicate that the intelligent teaching mode combining rain classroom live streaming teaching with MOOC+SPOC has increased students' interest in learning， reflecting a student-centered approach.

Keywords： smart teaching model; MOOC; SPOC; rain classroom; Probability Theory and Mathematical Statistics

概率论与数理统计是独具特色的一个数学分支，是理、工科学校一门必修公共基础课程。该课程将单纯的确定性思维模式推进到确定-随机性思维模式，这个特定的模式和课程内容使其在自然科学、管理科学和社会、经济等领域应用十分广泛[1-2]。通过对该课程的学习，既为后继专业课程的学习奠定了基础，亦为数学应用开拓了空间。同时对培养学生的逻辑思维能力、分析解决问题能力、数学建模能力尤为重要[3]。MOOC（Massive Open Online Courses），即大型开放式网络课程[4]，这种大规模开放式网络课程体现了高端的知识交换，使得每个学习者可以在任何地方、用任何设备进行学习[5]。SPOC（Small Private Online Course），即小规模限制性在线课程，达到要求的申请者才能被纳入SPOC课程平台。为充分发挥SPOC的优势，培养“互联网+”时代大学生所具备的能力，王晓春[6]构建了基于SPOC的大学课程对分教学形态，并给出了对分教学模式。

随着信息技术的高速发展和广泛使用，一些学者将MOOC和SPOC融合，提出了新的教学模式，方茹等[7]以MOOC资源为教学内容，以SPOC平台为教学环境，以翻转课堂为教学方法，针对概率论与数理统计实施了混合式翻转课堂的教学模式。张兰兰[8]根据高职院校学生特点与高等数学课程的教学经验，结合传统教学，辅助SPSS（Statistical Product and Service Solutions）等统计软件，进行了MOOC+SPOC混合式教学实践。孙中红等[9]在分析MOOC+SPOC混合式翻转课堂教学的优势及教学过程中可能出现的问题之后，提出了基于MOOC+SPOC混合式翻转课堂线上教学组织与管理模式，并介绍了新冠感染疫情下线上授课具体实施过程。孟桂芝等[10]将MOOC和SPOC结合，建立了工程数学混合式的教学模式，引导学生自主学习，激发学生的学习热情，提高教学质量，同时探讨了该教学模式的优劣。陈源[11]从教学准备、教学活动设计、教学评价设计三个维度，以政治学原理课程为例，实施了MOOC+SPOC混合式教学模式。

上述MOOC+SPOC混合式教学模式[7-11]一定程度上提高了教学质量，但教学过程未能充分调动学生学习积极性，而且整个教学过程主要针对课堂或者线下的学生，并未考虑到课外或者线上的学生，一定程度上未能真正的以学生为中心。在“互联网+”时代，如何将各种在线资源和信息技术同概率论与数理统计教学融合起来，兼顾课内外的每一名学生，培养其解决实际问题的能力，真正做到以学生为中心。鉴于此，我们将依托雨课堂智慧教学工具[12]并结合丰富的MOOC资源和SPOC平台，对概率论与数理统计课程实施MOOC＋SPOC＋雨课堂的融合式智慧教学模式。

一  基于MOOC＋SPOC＋雨课堂的融合式智慧教学模式

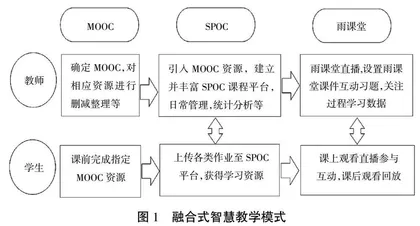
从2020年春季学期开始，在了解和逐步使用学堂在线MOOC后，结合辽宁工程技术大学（简称“我校”）学生特点，开展异步SPOC教学更为适合我校学生状况。在课堂教学环节，选择雨课堂智慧教学工具进行推题、融合式直播教学、讨论、翻转课堂等SPOC具体举措，效果不错。同时，雨课堂可以将直播视频、练习题目等资源在SPOC平台上进行沉淀，形成新的MOOC资源，极大地促进了MOOC资源的丰富。MOOC、SPOC、雨课堂环环相扣，相辅相成，如图1所示。这种基于MOOC＋SPOC＋雨课堂的融合式智慧教学创新模式体现了以学生为中心，以教师为主导的未来高校学生学习的主流趋势。

（一）  MOOC＋SPOC＋雨课堂直播

概率论与数理统计课程选择的MOOC资源为学堂在线精品课程资源。课程资源内容详细易懂，适合我校学生进行学习。教师在每周末发布下一周学生必须要预先观看的视频内容，学生也可自由在对应网站进行浏览和有计划地学习，积极开展课前MOOC资源学习。其余学习过程均可纳入到自建SPOC平台，教师每周会在同学们学习相应MOOC资源后，通过雨课堂抛出3～4个与本课内容相关的问题，让同学们思考和解决。课堂上，采用雨课堂全程直播授课，方便教室内外同学实现线上线下融合式教学。课程直播后自动沉淀到雨课堂中，学生可以随时观看课堂回放。课后，继续通过线上答疑解惑追踪不太理解的问题，从而实现SPOC闭环学习过程。

（二）  融合式智慧教学设计

雨课堂教学设计包括每周授课计划、课前小测、课前导入、课堂讲解、课堂活动、分组讨论、课后作业和课后测试等部分。在周末，教师会把下一周的授课计划提前发给学生，让学生了解课程将要学习的主要内容。授课计划中可推送MOOC资源。课前小测一般包括2～3个选择题或填空题，是为了检测学生是否掌握上一堂课学习的内容和掌握程度而设计的。根据学生的回答情况，教师进一步调整本节课的授课进程和讲解速度。通过案例式教学、疑问式教学、讨论式教学等多种方式，激发学生的兴趣，导入新课。在课堂授课环节中，将课程内容制作成PPT，开启雨课堂直播授课后，学生在手机端可以看到课程PPT，并可以把自己的听课想法或问题通过弹幕或投稿的方式与教师和其他同学进行互动和交流。教师的讲授要有系统性，调理清楚，重点突出，所用语言要清晰、简练、准确及生动。要根据内容的需要恰当地运用黑板或雨课堂白板，雨课堂白板书写后可截图发给学生。在课堂上，根据课程内容的需要，可以利用雨课堂随机分组，进行课堂讨论等各种课堂活动。启发学生的质疑能力，激起学生思维的浪花，燃起学生求知的欲望，鼓励学生团队协作的精神。教师把预先设计的各种题目推送给学生，边讲边练，讲练结合，实现知识水平和能力目标的双达成。学生如果在某个问题上纠结不解时，可以在手机端PPT系统中标注听不懂，教师端看到后可及时解决相关问题。课堂授课结束后，通过设置课后作业、课后测试等方式巩固和检测学生的掌握程度，加深学生对所学内容的理解。

（三）  融合式智慧教学案例

下面是2022学年秋学期教师组织的一次融合式智慧教学案例，教学内容为“中心极限定理”，班级为网络2021级1、2、3、4班和智能2021级1、2班。

教学思想是从本质上理解中心极限定理，这个定理描述的是大量独立同分布的随机变量的和服从或近似服从正态分布。在授课过程中，注重课程思政教学，培养学生的辩证思维，掌握从量变到质变的规律，学习科学家刻苦专研精神，鼓励学生勤奋学习。

课堂上教学进程采用BOPPPS模型[13]，同时通过雨课堂直播授课实现线上线下融合式教学。导言（Bridge-in）环节通过考察炮弹命中点与靶心距离的偏差来展开中心极限定理的背景引入，同时通过参加学习概率班的人数和开设班级数这一案例来导入拟研究的问题——若某个随机变量是由大量相互独立且均匀小的随机变量相加而成的， 如何研究其概率分布。以学生为中心，激发学生想解决这个概率分布的兴趣。目标（Objective）是理解中心极限定理的思想，会用独立同分布中心极限定理做近似计算，积极鼓励学生向科学家那样热爱学习，勤奋学习。前测（Pre-assessment）环节的设计，考察学生对于特定分布如泊松分布的掌握完成情况，以及学生对于将要学习的内容的自我理解程度，方便教师迅速调整接下来的教学内容，实施针对性教学，正确率达到83%，反映出学生较好地掌握了预习知识。以上三个环节都是通过SPOC平台提前发布给学生进行课前预习。

参与式学习（Participatory Learning）体现课堂教学的核心内容，以学生为中心，要让学生全部参与。从大量的相互独立的服从二项分布和泊松分布随机变量和的概率分布图中，引导学生观察其与正态分布的近似。从而抛出本课程核心思想和内容——中心极限定理，强调定理的使用条件和结论的用处，即在独立同分布的条件下，大量独立的随机变量的和近似服从正态分布。让学生思考，如何使用该定理解决引例中提到的问题呢？照顾到课堂上的每一名学生，学生的基础不同，接受能力不同，对于学生的个性化提示和指导也不同。做到有问有答，讨论互动，这是一个有温度的课堂。通过和学生一起观看高尔顿板试验，引领学生进一步理解独立同分布中心极限定理的作用和意义。

对于二项分布，它对应的中心极限定理为棣莫弗-拉普拉斯中心极限定理。学生在学习独立同分布的中心极限定理和棣莫弗-拉普拉斯中心极限定理内容后，教师设置相关实际背景的问题加以练习，巩固学生对于定理的理解和应用。使学生们感受到即使不知道随机变量的精确分布，其和在一定条件下也会服从正态分布。可以这样理解：积少成多，从量变到质变。质变的发生是以量变的积累为基础的。就像荀子在《劝学篇》所说，“不积跬步，无以至千里；不积小流，无以成江海”，意为做事情如果不一点一点积累，就永远无法达成目的。