大学数学学习之认知错误分析

摘  要：全面完整地掌握学习者的学习能力或学习状况，是开展教学研究的重要起点。研究者以质性与量性研究相结合，归纳分析了405名大二上学期理工科背景的学习者对数学概念题的作答结果，在错误类型鉴定的基础之上，运用多元度量与聚类分析之整合模式，对其知识结构图进行个别化分析，搭配访谈资料，从中归纳出线性代数学习的六大核心概念，并进行认知诊断分析。最后，以线性代数学习情意量表为辅助，依据各样本的解题表现，搭配错误类型进行分群。通过聚焦学习教材的核心概念并给予合适的权重，计算加权分数搭配知识结构图、数学学习情意量表，来确认学习者的迷思概念，以作为后续补救教学的根据。

关键词：多元度量；聚类分析；线性代数学习；认知错误诊断；补救教学

中图分类号：G642      文献标志码：A          文章编号：2096-000X（2023）06-0105-04

Abstract： Understanding learners' capability or learning situation exhaustively， is an important starting point of teaching researches. The researchers summarized 405 sophomores' solutions on mathematics concept questions by qualitative and quantitative research methods. At the base of judgments on errors types， we integrated multidimensional scaling and cluster analysis to analyze their knowledge structure. Meanwhile， we generalized six core concepts of linear algebra by arranging interview materials， and examined each knowledge structure graph consequently. Finally， at the aid of linear algebra learning affects scale， we grouped all of the students according to solution answers and errors types. Through suitable ratios of core concepts， knowledge structure graph， linear algebra learning affects scale， and calculating weighed scores， we determined learners' misunderstanding concepts to obtain foundation of remedial teaching in the future.

Keywords： multidimensional scaling; cluster analysis; linear algebra learning; cognition error diagnosis; remedial teaching

线性代数是以向量空间、线性方程组为主要研究对象，以矩阵、行列式为重要基础工具，处理对象间线性关系的学科。作为一种解题工具，这种基本的数学理论在许多课程上被普遍应用。尤其对于主修工程、数学、统计、土木建筑和其他自然科学的学习者而言，它更是必备的知识。作为大学数学重要的基础课程，线性代数建立在向量空间理论基础上，以线性变换为其核心运作机制，是大学数学抽象性、形式化与实用性的典范。然而，正是这门继高等数学之后的后续课程，对不少同学而言，并不是点燃了其对大学数学的学习兴趣，而是由于接触此课程后对后续课程的学习产生了困扰。事实上，在线性代数教学现场，缺乏“人、地、时、事、物”的传统教学，局限与障碍日益凸现。1990年1月线性代数课程研究小组（Linear Algebra Curriculum Study Group），在美国国家科学基金（NSF）的支持下成立，旨在持续激发研究者与实践者对本科生线性代数课程的兴趣，并提高其教学质量[1]。同时，部分研究者从认知诊断分析入手，通过知识结构图分析找出学习者的核心概念，旨在能更正确地描述学习者的实际能力，为教师补救教学及教学研究提供了科学的研究起点[2-3]。

一  研究目的

单一的认知诊断工具，满足不了完整刻画学习者学习状况的需求。为了能有效地了解学习者的迷思概念和知识盲点，提升国内线性代数的教与学，本研究在专家对错误类型鉴定的基础上，辅助以线性代数学习情感量表，搭配访谈资料，通过多元度量与聚类分析的整合模式，对学生进行适当的分群。除了有效分群以外，本研究对不同学生的知识结构图进行了比较，并准确把握个体与各群之间的关系。此施测结果，可以为教师补救教学及线性代数的教与学提供科学依据。研究方法整合了多向度量尺、聚类分析和试题反应理论观点，以结构化的图像和学习情感分类来全面地展现每一集群中学习者的内在知识结构。

二  文献探讨

学习者在学习过程中注意力不集中或者记忆不牢固，会对知识产生误解（mistakes）或混淆。而认知过程中的错误（errors），却揭示了学习者相关知识的不足，是由于对基本事实、概念和技能掌握不够造成的[4]。进一步地，在新创设的学习情境中，它与想象力和创造力紧密相连，因此，在很大程度上影响甚至决定着学习者能否做到不同领域知识间的相互连结。数学教学过程中，不可避免地学习者会出现这样或是那样的认知错误。教育研究者和实践者不能一味地害怕或回避学生错误的出现，而应该营造学生能够呈现自身认知错误的合适的情境和场域，然后从方法论上对其进行补救和纠正。

（一）  数学学习过程中的错误研究

数学教育中学生出现的错误，并不是情境的偶然，也不是单纯地由于学生的不确定和粗心而出现的结果。它产生于数学结构本身，或者是数学课堂上前期教学的产物。通常情况下，如果教师不从教学法上对其进行干预，这些学生的认知错误能持续数年。简单地说，错误分析从两方面获得了人们的重视。一方面在于，它能诊断学习困难，更多地了解学生的能力，提高学习成绩，从而改进教学；另一方面，它是数学教学过程研究的重要起点，是一种相当有前景的教育研究策略[5-6]。

通常情况下，在教学实践和数学课堂分析中，研究者把数学上的错误（mathematical errors）和教学法上的错误（didactic errors）区分开来。数学上的错误是指学习者在某个特定的时刻把不正确的数学陈述认为是正确的，或是从数学的立场为不正确的陈述维护其合理性。教学法上的错误意味着一种情境，在这种情境中，教师的行为与教学法、方法论和常规准则相背离。在情境为基础的数学任务中，这两种错误的类型有时显得更为突出[7]。无论是理解任务本身、把任务转换成数学问题，还是操作数学程序、解码并解释研究结论在现实情境中的意义，都更加需要跨领域知识间的连结。连结是一种极其重要的能力，在数学课堂实践中，教师只关注发展学生概念的内部连结是不够的，更要注重应用的、延拓的外部连结。与连结有关的两个指标性文件，分别是1989年NCTM（National Council of Teachers of Mathematics， 美国数学教师学会）[8]提出的课程标准和荷兰的RME（Realistic Mathematics Education， 真实数学教育）[9]。

（二）  知识结构的心理计量

传统纸笔测验的分数，不能完整说明学习者的真实能力或学习情形，拥有相同分数的不同学习者，其知识结构图可能是不同的。从实证研究文献可知，径路搜寻、多向度量尺和聚类分析是知识结构图心理测量常用到的方法[10]。这三种方法各有功用和自身独到的价值，而不同方法的联合使用则相辅相成，对知识结构的探究有重大的助益[11]。多向度量尺从整体观点，叙述语意概念距离的空间性，在较低维的欧氏空间把客体的相似程度用图形表达出来，从而揭示客体之间的真实结构关系。集群分析方法，根据语意概念之间的距离远近，能化繁为简做一个适当的组别归类，并给予每个组别一个适合的命名。整合多向度量尺和聚类分析方法，可以互补讯息的不足，适合于对编制的试题进行内容效度分析。根据多向度量尺所分析的结果，可以得到适当的维度来解释这些概念。每个维度可加以命名，而这些坐标表示各个概念在各个维度上的位置，也可据此判断在该维度上的重要性。但是，多向度量尺不能把概念做适当的分类，所以我们可根据多向度量尺分析所获得的各概念坐标资料，来进行聚类分析，将概念加以群组化。根据分析所得的集群的特性，必要时可将集群予以命名。就聚类分析而言，一般以群平均法及Ward法较为精准，经常被一般研究者使用。在认知结构的大量分析文献里，诸多研究是采用阶层集群分析方法，因为其结果可以看出概念群组之层级性。在SPSS 提供的常用距离模型中，多维尺度分析还有一些其他的缺点：一方面，它们受各指标的量纲影响;另一方面，它们没有考虑指标之间的相关性。因此，在进行多维尺度分析时，要尽量解决和避开这些缺点，特别是指标之间的相关性问题。

三  研究方法

本研究的具体工作是从理论和实践两个方面，进行线性代数学习认知的诊断与研究。研究学校位于中国西部汉族和蒙族的聚集地，是一所以培养理工科背景学生为主要任务的综合类高校。在考查学生对线性代数主要内容掌握程度的初探性研究基础上，透过405位非数学类专业大二上学期学生参与封闭结构试题的有效作答，进行多元度量与聚类分析，并辅助于线性代数学习情感量表的口头和文本资料，来探讨学习者线性代数学习能力的分类。这些学生在施测过程中均为有效样本，他们在校内均系统完整地学习过线性代数课程，就其所就读的科系类别而言，可区分为土木工程、能源动力、环境科学、工业工程、测量控制和企业管理六大类别。

本研究的测量工具共分为两部分，第一部分为数学概念题，用于分析不同专业背景的学习者对线性代数这门学科的实际掌握能力。以常用统计套装SAS和SPSS作为主要的软体分析工具，经过信度考验，15个独立题项的Cronbach's Alpha值达.85。参考前期初探性研究的资料，题项经由7位试题审查委员编写，并听取3位在职工科数学讲师的意见，最终将试题编制、修正完成。第二部分为线性代数情感量表，区分了对数学的情感和对数学学习的情感，并将数学学习情感界定为以下九个子构念：对数学成功的情感、家庭文化、学校氛围、教师情感、数学的跨学科性、数学的实用性、学习数学的兴趣、数学焦虑和学习动机。在实际应用上，尽量克服由于测量题目过多，而导致在短时间内无法了解一个班级或者学校对数学或数学学习的情感的局限性。

四  结果与讨论

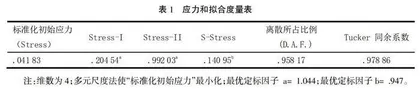
表1是模型拟合优度的基本情况，该表中指标stress 的值为0.041 83，另一指标Dispersion Accounted For（D.A.F.）（类似于经典部分的RSQ）的值为0.958 17，表明模型的拟合效果比较好。研究者将受试者所有可能的错误类型，经由专家鉴定后，依据各样本的解题表现，搭配错误类型以进行分群，作为日后分群补救教学的依据。分群分析的目的在于对文本资料进行有意义的分群，以有效地使用该资料，基本理念在于经过适当分群后，使同一群内的有效样本同质性较高，而不同群集之间异质性较高。分群的阶段性成果包括线性代数学习的核心概念、认知分析及五类知识结构图类型。

线性代数学习的六大核心概念包括以下内容。①矩阵的运算与性质。包括矩阵的加法、乘法、运算规则、矩阵转置、逆矩阵和三种初等变换。学习过矩阵加减法及数乘运算以后，学生对矩阵与矩阵之间乘法的“自然方式”产生期待。国内线性代数教材所介绍的矩阵的乘法规则及应用价值对学生来说，是一个挑战[12]。学习者在学习“矩阵的乘法”的过程中，若对于矩阵乘法的产生、规则及其价值没有清楚地认识，常常会产生以下困惑：矩阵为什么要这样乘？实际的工作生活中，矩阵乘法的用途体现在哪里？样本中的受测者对于较复杂矩阵的乘法，出错的概率较大。②行列式的计算。行列式运算的三种方法、行列式的性质和克莱姆法则。学习者缺乏必备概念知识，将导致不当的召唤程序。受测者因认识不清楚，经常发生误用公式或规则的情形。如四阶及四阶以上行列式的计算，误用二阶和三阶行列式的对角线法则；将矩阵的运算规则误用于行列式之上，数乘以行列式等于数乘以整个行列式的所有元素。从受测样本的答题情况来看，一些从数学本身来看非常简单和明显的事实，在线性代数教学中却并非如此。③线性方程组的求解。包括线性方程组解的结构和判定、基础解系的性质以及解法。样本资料显示，学习者对基础解系的由来和求法倍感陌生。缺乏具体化操作的线性代数教学，使学生无法建立数学概念知识与程序知识之间的关联。同时，在求解线性方程组时，对系数矩阵（增广矩阵）作初等变换化为阶梯形矩阵时，误用了初等列变换。④向量组的基。包括向量空间中线性相关性、矩阵的秩、向量组的基、向量在不同基下的坐标和内积。向量空间是线性代数的主要研究对象和核心运作机制。从施测样本资料来看，线性相关、最大线性无关组等非机械性的概念知识，会给学习者带来更多的认知负荷。在广泛的应用领域中，从欧氏空间类推到Rn空间，需要恰当的教学活动设计来化解一般知识概念的抽象性与形式化。⑤二次型的标准型。利用正交矩阵化实对称矩阵为对角矩阵的方法，求解二次型的标准形式。相比于配方法和初等变换法，这种方法再次用到矩阵特征值和特征向量的概念，这需要学习者对相关概念有足够的熟悉度。⑥方阵的特征值与特征向量。包括方程组的求解、相似对角化的条件和方法。从有效样本资料来看，在完整解决问题的一些重要节点上，能有效使用数学概念并建构长期记忆的程序知识，显得至关重要。因此，在引入几何例子的基础上，搭配学习者专业上的实作经验来介绍特征值与特征向量，是一种改进了的教学策略。鉴于仅仅依靠纸笔测验的分数，不能全面刻画学习者的学习状况，如果聚焦学习教材的核心概念并给予合适的权重，计算出来的加权分数搭配知识结构图、数学学习情意量表，可以确认学习者可能的迷思概念，以作为补救教学的依据和参考。