五阶递进的最短路径问题教学模式探索

摘  要：最短路径问题是计算机科学、地理信息科学、运筹学、管理科学、交通工程、工业工程和复杂系统科学等领域的基础性问题，也是许多相关课程中的教学重点。针对目前教学中存在的被动接受、手工计算、只算不用等问题，按照“精选算法、纵向到底、横向到边”的教学理念，探索“算法原理—数学建模—应用举例—程序实现—算法比赛”五阶递进的最短路径问题教学模式，有助于培养和提升学生的原理掌握深度、优雅学术品位、运筹优化思维、综合应用能力和团队合作精神。

关键词：图论；最短路径；数学建模；Dijkstra算法；应用举例

中图分类号：G642      文献标志码：A          文章编号：2096-000X（2023）32-0032-04

Abstract： The shortest path problem is a fundamental problem and a core knowledge module in many disciplines， such as computer science， geographic information system， operations research， management science， transportation engineering， industrial engineering， and complex system science. It is also the focus of teaching in many related courses. According to the teaching concept of "selecting algorithms， vertical to the end， horizontal to the edge"， this paper explores the five-step teaching mode of "algorithm principle - mathematical modeling - application example - program realization - algorithm competition" for the shortest path. It is helpful to cultivate and enhance students' in-depth grasp of principles， elegant academic taste， operation and optimization thinking， comprehensive application ability， and team spirit.

Keywords： graph theory; shortest path problem; mathematical modeling; Dijkstra algorithm; applications demonstration

基金项目：上海高校市级重点课程建设项目“《运筹学》”（无编号）；上海高校课程思政领航课程建设项目“《运筹学》”（无编号）

第一作者简介：许项东（1985-），男，汉族，安徽霍山人，博士，教授，博士研究生导师。研究方向为交通运输网络建模与优化、交通系统韧性。

最短路径问题的目标是，在网络中给定两节点之间找出一条总权重之和最小的路径[1]。作为图论中最为经典与最常见的问题之一，最短路径问题是计算机科学、地理信息科学、运筹学、管理科学、交通运输工程、工业工程和复杂系统科学等领域的研究理论基础，其核心思想与日常生活中的交通导航、救灾抢险、工程管理等密切相关，成为许多相关课程的教学重点。

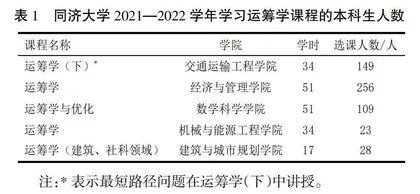
最短路径问题是运筹学课程的基本内容和教学重点。以同济大学为例，如表1所示，开设运筹学课程的学院和专业主要有：交通运输工程学院的交通工程、交通运输专业，经济与管理学院的物流管理、信息管理与信息系统、市场营销等专业，数学科学学院的统计学、数学与应用数学专业，机械与能源工程学院的工业工程专业等。需要指出的是，这里仅统计了运筹学类课程。其他课程中也可能涵盖最短路径问题，如计算机相关专业的数据结构与算法课程。

由于最短路径问题模型目标明确、求解算法启发性强、与其他问题结合度高及应用场景广泛，是一个培养创新思维和实践能力的绝佳教学点。然而，在目前的最短路径问题教学中，“被动接受、手工计算、只算不用”的问题仍普遍存在，学生们的综合能力与应用水平有待提高。在内容上，重课本轻实践，实际问题的数学抽象能力较弱[2-3]；在思维上，重解题轻原理，只会快速解题而举一反三能力欠缺；在方法上，重手算轻程序，不会主动应用计算机与先进工具来辅助求解[4-5]。上述问题使得我们的教学实际效果难以满足新时代对高校人才培养的要求，尤其是与研究型大学培养创新精神与实践能力兼备的人才目标存在较大差距[6]。本教学团队经过多年的教学探索和迭代反馈，初步形成并较为成功地实践了可复制可推广的“算法原理—数学建模—应用举例—程序实现—算法比赛”五阶递进的最短路径问题教学模式，以期给其他有类似问题的本科课程教学以方法上的参考。

一  五阶递进的最短路径问题教学模式

针对现有最短路径教学中存在的问题，我们基于“精选算法、纵向到底、横向到边”的教学理念，提出了“算法原理—数学建模—应用举例—程序实现—算法比赛”五阶递进的最短路径问题教学模式，如图1所示。其中，“算法原理、数学建模、应用举例”主要为课内教学部分，从概念到方法再到实例，由浅入深、层层递进。考虑到最短路径算法谱系较为复杂，通过“精选算法”，为学生讲细讲透一种经典算法原理，夯实基础理论。按照“纵向到底”的理念，深入介绍其数学规划模型与实际应用，帮助学生深化理解算法。“程序实现、算法比赛”则为课外实践部分，基于“横向到边”的思想，从小规模测试网络的算例实验，到大规模真实网络（所在城市的道路交通网络）的算法设计与优化，引导学生化被动为主动，注重提升学生的实践应用能力与创新思维，以及加强与前修课程的综合理解。通过课堂内外相互促进、相互结合的形式，形成五阶递进的最短路径问题教学模式。

在最短路径问题引入方面，考虑到笔者的课程教学对象是交通运输工程学院的本科生（包括交通工程专业、交通运输专业），我们引入了日常生活中常用且也是交通运输工程的前沿应用场景——车辆路径导航（包括未来自动驾驶的路径导航）。

最短路径问题的具体算法有着较为丰富和成熟的谱系，可按照以下三类进行细分[7]：①问题类型（Problem Type），如针对单源最短路径的Dijkstra算法，针对多源最短路径的Floyd算法；②输入网络特征（Input Network Characteristics），如针对无向网络的Minty算法、针对整数弧长的Dial算法；③求解策略（Solution Techniques），如针对网络变化时最短路径更新迭代的Loubal算法、应用模拟计算机技术的Klee算法等。

在教学实践中，我们遵循“精选算法、纵向到底、横向到边”的教学理念。其中，“精选算法”指的是，我们在课堂教学中重点介绍最为经典且常用的Dijkstra算法，对其他算法只简单提及，留给学生课后自学和拓展；“纵向到底”指的是我们不仅讲授Dijkstra算法的执行步骤，更启发学生理解算法基本原理和数学规划建模过程，引导学生品味该算法的创新之处和优雅之美；“横向到边”指的是，我们引导学生利用熟悉的计算机语言来编写Dijkstra算法的代码，结合大规模真实交通网络，挖掘算法结果所蕴含的管理洞见，并通过以小组为单位的算法比赛培养和提升学生的综合应用能力、团队合作精神。

经过多年的教学实践，在算法原理环节提升了学生的优雅学术品位；通过介绍最短路径问题的数学规划建模，引领学生形成看透问题本质的意识；通过贴近专业方向的多个应用举例，帮助学生开拓联想创新思维；通过程序实现，锻炼学生的综合应用能力，再通过算法实现，积累了学生团队合作与创新实战经验。

二  教学设计与实践

（一）  算法原理——优雅学术品位

在算法原理部分，我们依循经典运筹学教材的讲解思路，介绍最短路径问题的数学定义、经典Dijkstra算法（包括适合初学的图上作业法、适合程序实现的表上作业法）等。在介绍算法原理的同时，我们注重引入算法的发展演化历史，引导学生思考不同算法的优缺点和适用条件，培养学生的优雅学术品位。如用枚举法亦可找到最短路径，但并不高效，计算机技术的进步催生了更简便高效的算法，使得最短路径问题的求解更加简洁巧妙。

（二）  数学建模——探求问题本质

在现有的经典运筹学教材中，最短路径问题部分少有介绍其数学规划模型，我们在教学中适度介绍最短路径问题的数学规划模型。之所以在教学中涉及最短路径问题的数学建模，是为了帮助学生进一步了解最短路径问题的本质，深化对最短路径算法的理解。在研究现实世界的很多复杂问题时，通常是先进行数学建模，然后针对模型开发高效的求解算法。

作为数学规划模型，涉及变量、目标函数、约束条件等三要素。在教学中，引导学生思考最短路径问题的变量、目标函数、约束条件分别是什么。决策变量的选取，直接决定模型是否需要计算量和存储量高昂的路径枚举。按照最短路径问题的定义，一般将表征每个边是否被选入最短路径的0-1整数变量作为求解变量，目标函数是全网所有被选中边的总成本最小，约束条件需要确保所有被选中边可以构成从起点到终点之间唯一的一条路径，即从起点有且只有一条边被选中，中间节点（非起点、非终点）的流入和流出守恒，进入终点有且只有一条边被选中。尤其要关注，该模型的0-1整数求解变量可等价松弛为非负连续变量，从而将0-1整数线性规划问题转化为更易求解的线性规划。引导学生体会，在对模型进行求解前，非常有必要“三思而后行”，避免“Garbage in， garbage out”现象，尽可能降低模型的复杂性，在算法的通用性和定制化之间作出合适的取舍。

（三）  应用举例——联想创新思维

根据笔者的科研经历，学习经典问题的目的可能包含：①学习经典问题的创新思想，丰富自己解决问题的工具箱（toolbox）；②现实中遇到的问题往往比经典问题更加复杂（例如，电动车的路径规划、自动驾驶车的路径规划），需要针对这些问题的特征，对经典问题的模型和算法进行二次创造；③将看似没有关系的其他问题“转化”为经典问题，这需要对经典问题有着深刻的理解。

针对我们的教学对象——交通类本科生，我们设计了多个应用举例。

1）路面更新问题：道路路面每年的养护费用和阶段性大修费用随路面使用年限的增加而变化，需要决策在路面设计年限里的更新计划，使得总费用最小。

2）火车售票处选址问题：现准备在七个居民点中设置一个售票处，已知各点之间的距离。问售票处设在哪个居民点，可使最大服务距离最小？若设置两个售票处，应设在哪两个居民点？

3）“全有全无”交通分配问题：已知某城市各交通小区之间的出行需求和路网（包括各条道路上的行程时间）。需要把这些出行需求按照行程时间最少的路径（即全有全无）分配到路网各条道路上。

4）几类限制条件下的最短路径问题：如，找一条不通过某些边的最短路径，可对应于货车限行、外牌通行、规避事故等情形下的路径规划。

需要指出的是，以上这些应用场景和应用举例与学生后续的专业核心课程密切相关。当然，针对不同专业的学生，需要增强应用举例问题场景的针对性，以提高学生的代入感、认同感以及与后续专业课的衔接性，培养学生的完整知识体系。

在课后作业的设计方面，除了Dijkstra算法本身的巩固练习外，我们也设计了最短路径应用问题建模方面的作业。

（四）  程序实现——综合应用能力

我们在教学中引入“程序实现”环节，引导学生从程序设计角度进一步理解最短路径问题的求解原理，同时增强学生学以致用、善用计算机工具的综合能力。据笔者了解，在许多专业的课程安排中，运筹学的课程学习节点往往处在通识基础课与专业核心课的衔接段，加入“程序实现”部分可更好地起到知识能力上的承前启后作用，尤其是与计算机编程、数据结构、算法设计等前序课程的衔接，以帮助学生搭建更为完整的知识体系。