分段快速排序在硕士研究生招生考试中的应用

摘  要：硕士研究生招生入学考试作为进入硕士研究生学习必须进行的考试，是国家重要教育考试之一，同时也是《国家中长期教育改革和发展规划纲要（2010-2020年）》的一项重要工作。随着研究生学历层次的普及，我国的研究生教育事业得到飞速发展。然而，快速发展的同时也给高校硕士生招生工作带来很多问题，例如，面临自命题科目增加，报考人数巨增，资源受限无法适应新形势等。文章针对硕士研究生招生工作中的试卷整理环节，探索分段快速排序在该环节中的实际应用。实践证明，相比传统直接插入排序，文章应用分段快速排序的时间复杂度降低了一个数量级，并且在实际应用中取得较好的效果。

关键词：硕士研究生;招生考试;分段快速排序;试卷整理

中图分类号：G643      文献标志码：A          文章编号：2096-000X（2022）23-0023-04

Abstract： Postgraduate entry examination is a national-level and indispensable examination for the postgraduate student study. Meanwhile， it is also an important task in the on the guidelines of the national program for medium- and long-term educational reform and development for China（2010-2020）. The postgraduate education of China has a fast development with the popularization and widespread of the postgraduate degree. However， the fast development also brought a serious of problems for the college postgraduate enrollment， e.g.， increasing independent proposition subjects， increasing examination applicants and limited resources with respect to the new situation. This paper focuses on the paper arrangement stage in the postgraduate enrollment and the application of sectional quick sort method in this stage. Results show that the time complexity of the sectional quick sort method is one magnitude lower comparing to the traditional straight insertion sort and the proposed method gains good performance in the postgraduate enrollment practice.

Keywords： postgraduate; entry examination; sectional quick sort; paper arrangement

一、高校硕士研究生招生意义

硕士研究生招生入学考试（以下简称“入学考试”）是考生进入我国研究生教育层次的主要渠道，其人才选拔效果影响着研究生教育的生源质量。随着1980年《中华人民共和国学位条例》[1]的颁布，我国的研究生教育事业得以迅猛发展，全国研究生的招生报考规模截至到2017年已经突破两百万人，2018至2020年两年增加了140万人[2]，受今年新冠肺炎疫情影响，预计2021年仍将大幅度增长。入学考试作为进入研究生教育的入口及重要环节，对整个选拔过程至关重要。同时，做好高校硕士研究生招生工作，推进素质教育实施和创新人才培养，促进学生健康发展、培育国家杰出人才，对维护社会公平、普及研究生学历层次有着重要作用。

当前，我国的硕士研究生招生考试历经过去几十年不断地探索与改革，已形成一套较为完善的管理运行机制。众所周知，现行硕士研究生招生考试主要实行初试和复试的综合选拔制度。初试的考核方式为笔试，笔试试题由全国统一命题统考科目与招生单位自主命题的专业考试科目等共同组成。其中，统考科目主要包括思想政治理论、外语等;招生单位自主命题的专业课程一般包括两门业务课程，主要考察考生对报考专业基础知识和综合能力的掌握;复试主要由笔试（可选）和面试等多种考核方式组成。部分高校在考生进入复试后采取多元的考核方式。高校同时作为招生单位和报名考试点（以下简称“报考点”），既要完成作为招生单位的试卷命制、寄送、回收、整理与组织阅卷、统计成绩、复核成绩等一系列工作，又要完成作为报考点的试卷接收、组织考试等一系列考务工作。然而，近年来硕士研究生报考人数的巨幅增长，给硕士研究生招生工作带来了沉重的负担，大部分高校的招考工作人员已经不能满足日益增长的工作量需求。因此，面临报考人数的剧增带来的系列问题，本文认真梳理研究生招生的各个环节，探索如何快速、准确、平稳地完成招生单位的招考工作，具有十分重要的意义。

二、高校硕士研究生招生工作现状

本文对国内部分知名高校进行了调研，与高校硕士研究生招考工作人员进行座谈，交流当前高校硕士研究生招生过程中相关环节的工作模式和经验。经过梳理，本文认为当前我国硕士研究生招生工作主要存在以下问题。

（一）资源受限，招考难以分离

调研发现，高校招考工作人员一般在3到6人之间。招生工作由于其高强度、高压力、零差错特点导致招考工作人员流动性大，新旧工作交替无法有效衔接，导致人力资源严重不足。同时招生考试过程中的设备设施条件无法充分保障，只能靠人工去完成这些环节（例如折纸机，将试卷对折），设备资源不足。

现行研究生招生考试制度下，招生单位除完成本单位招生工作以外，还需作为考点完成报考点的考务工作，招考难以分离[3]。

（二）业务重视不够，无法适应新形势

研究生入学考试作为国家级重要考试之一，涉及若干环节，每个环节都需要反复仔细地完成、检验等才能保证准确性。然而，随着研究生学历层次的普及，报考人数大幅度增加，招生单位对变化的业务情况重视不够，经验主义已然无法适应人数剧增带来的新问题、新形势[4]。

（三）自命题科目多，报考人数增加，试卷整理费时费力

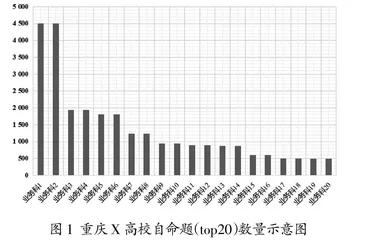
随着近年来硕士研究生报考人数的剧增，给招生单位的试题卷答卷小信封（以下简称“试卷小信封”）整理带来了巨大的影响。以重庆X高校为例，根据其2020年报考数据，该校报考人数约为2.8万余人，通过统计分析，该校自命题数量较多的top20科目如图1所示。可以看到单科自命题数最多已经高达4 500余人。当回收试卷小信封后如何快速地按照（考试科目代码-流水号）完成排序，对后续工作流程起着至关重要的作用。

三、分段快速排序在试卷整理排序中的应用

（一）试卷整理的常规做法

试卷小信封整理排序是研究生招生工作环节中的关键环节之一。所谓试卷小信封整理，即是将回收的试题答卷小信封按照（考试科目代码-流水号）排序后才能进入后续组织阅卷等工作。例如，以报考重庆X高校（简称X校）2020级考生数据为例，X校有140余个自主命题考试科目，有2.8万余人参加考试，这就意味着该校需要将5万余试卷小信封按自命题科目分类，然后将每个自命题科目类的若干考生试卷小信封按照该科目内流水号进行排序。

以某业务科考试科目（业务科1）为例，参加该考试科目的考生人数4 500余人（图1），排序工作首先需要从回收的5万余试卷小信封中查找并取出业务科1的试卷小信封4 500余个（本文不考虑该考试科目缺考的考生小信封需要单独挑选出去的情况，因为缺考考生数量相对于总共试卷小信封数量可以简单忽略掉），然后对业务科1全部4 500余个试卷小信封按照科目流水号进行排序。

常规做法即是使用直接插入排序算法进行排序[5]。例如，对于业务科1的试卷小信封，我们就是要把每个流水号为n的小信封都放到自然数n的位置，n∈{1，2，...，N}，其中N为该科目参加排序的试卷小信封个数，这样就完成了排序。直接插入排序仅适用于少量数据的排序，对于较大数据量排序使用直接插入排序的时间和人力成本消耗太高。因此，需要引入更加合理有效的排序方法，提高招生单位试卷小信封整理排序工作的效率，节省资源，更好地为后续工作环节服务。

（二）分段快速排序在试卷整理中的探索

1. 快速排序

快速排序（Quick Sort）[5]由C. A. R. Hoare在1960年提出。其基本思想：通过一趟排序将要排序的数据序列分成独立的两个部分，其中一个部分的所有数据都比另外一个部分的所有数据小（或者大），然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，直到排序完成。快速排序的流程如下：（1）首先设定一个分界值，通过该分界值将数组分成左右两部分。（2）将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边，完成一趟排序。（3）分别对左边和右边的数据独立排序。（4）重复上述过程，递归调用该流程，直到排序完成。

为了更加直观地理解快速排序的工作原理，假定有6个元素的数组A[]={10，6，3，5，32，1}，设定下标i=0，j=5分别指向数组的首尾元素，初始参考值设为数组第一个元素ref=10;此时，从数组后面j=5往前找，第一个比ref小的数是1，则此时的序列为{1，6，3，5，32，10}，i=0，j=5，ref=10;然后从数组前面i=0往后面找，第一个比ref大的数为32，因此序列为{1，6，3，5，10，32}，i=4，j=5，ref=10;此时从数组后面j=5往前面找，只有j=4以后的数比10小，此时，i=j=4，ref=10成为一条分界线，ref以左的数均小于等于ref以右的数;分别对ref左右两部分数组递归调用上述流程，直到得到{1，3，5，6，10，32}，见表1。

2. 分段快速排序在试卷整理中的应用

本文探索快速排序是否在试卷小信封整理排序工作中得到有效应用。仍以上述数据为例，若直接将业务科1的试卷小信封4 500余个使用快速排序，虽然比直接插入排序时间复杂度降低了一个数量级，但实际上快速排序不具有可操作性。一是因为数组数据量太大，不利于操作;二是现实情况下保密场地面积有限且不利于工作人员并行工作。

基于上述问题，结合实际可操作性等因素，本文提出改进的快速排序分段快速排序，即将长度较大的数组先按照一定规则分割成若干长度较小的数组，然后针对各小数组应用快速排序。分段快速排序的流程如下：（1）获取需要排序的数组长度（N）;（2）根据实际情况制定每堆长度（L），同时获得堆数T;（3）将大数组按照既定规则分到每堆;（4）分别对每堆递归调用快速排序算法得到每堆排序数组;（5）按照堆的顺序合并数组得到最终排序结果。

为了更直观地理解分段快速排序在试卷小信封整理排序中的应用，本文仍以业务科1的试卷小信封为例，根据分段快速排序的流程，首先获得需要排序的试卷小信封长度为4 500余个;其次本文设定将4 500余个信封分割成每段（堆）100个试卷小信封并且获得总堆数为45堆;然后安排工作人员根据每个试卷小信封的流水号放至到对应的45堆中（第1堆对应试卷小信封为第1至100个，第2堆对应的试卷小信封为第101至200个，以此类推，…）;然后对每堆堆内递归调用快速排序算法，得到有序堆;最后，按照第1堆、第2堆、…、第45堆的自然顺序合并，得到最终4 500余个有序试卷小信封，排序完毕。