数学本原性问题提出教学初探

摘 要：数学教学中，本原性问题提出教学作为一种问题提出教学方式，是鉴于问题提出教学困境提出的。“数学本原性问题”是指能激起学生“刨根问底”的探究欲望，并能引领学生探究数学本质内涵的“最根本、朴素的观点、思想与要领”的问题。数学本原性问题提出教学能培养学生的好奇心和刨根问底的精神，发展学生的元认知和数学一般性观念，提升学生的创新意识和理性精神。以“二面角”为例，说明开展数学本原性问题提出教学的基本路径：明确数学本原性问题；引导学生提出数学本原性问题；利用数学本原性问题驱动探究性学习。

关键词：高中数学；问题提出；本原性问题；二面角

一、 从问题提出教学到本原性问题提出教学

所谓“问题提出教学”是指，引导学生在给定的情境中或在解决问题的过程中提出新的问题，进而利用所提问题驱动探究学习进程的一种教学方式。一方面，让学生提出问题是教学目标，即培养学生发现和提出问题的能力——“提出一个问题往往比解决一个问题更为重要，提出新问题需要创造性的想象力，而且标志着科学的真正进步”［1］。另一方面，让学生提出问题也是教学手段：由学生提出的问题开展教学，可以激发学生的学习动力，帮助学生深入理解知识技能，感悟思想方法——“问”是“思”和“学”的起点。

相应地，“本原性问题提出教学”是指，引导学生在给定的情境中或在解决非本原性问题的过程中提出本原性问题，进而利用所提本原性问题驱动探究学习进程的教学方式。本原性问题提出教学作为一种问题提出教学方式，是鉴于问题提出教学困境提出的：问题提出教学不应当让学生提出对知识技能机械记忆的问题或简单模仿应用的习题，也不应当让学生提出不着边际的问题，而应当让学生提出关乎主题的具有探究性的问题，从而促进学生更好地理解知识技能，感悟背后的思想方法。也就是说，问题提出教学要想取得更好的效果，就要引导学生提出本原性问题。这是由本原性问题的内涵决定的：本原性问题是其他问题（可称为派生性问题）的根本与源头。

“本原”是哲学中的一个术语，是指世界的来源和存在的根据，是希腊文arche或拉丁文principium的意译。古希腊哲人认为在生灭变化的万物中存在某种始终不变的东西，名之“arche”。本原是存在或生成或认识由之开始之点，是现象背后的基础，是事物存在和生成的质料，是认识成为可能的根本。［2］中国古人也常运用“本原”一词。《左传·昭公九年》中有：“我在伯父，犹衣服之有冠冕，木水之有本原，民人之有谋主也。”这里的“本原”即“本源”，有“根源、根本、根由”之意。《史记·秦始皇本纪》中有：“从臣思迹，本原事业，祗诵功德。”这里的“本原”有“推究，推本溯源”之意。马天骏教授曾围绕《论语·学而》“君子务本，本立而道生”一句中的“本”，阐发“本原”的一个隐喻网络，即“本原”“本质”“基础”“本源”“始基”“基质”“根本”“根基”“根源”“本根”“本始”“本初”“基本”“始原”“初始”“始源”“源本”“源始”“源初”“源头”“原本”“原始”“原初”等。［3］不少教育研究者和教师借用“本原”一词，应该是基于两点考虑：一是希望引导学生寻找概念、原理或理论等产生的根源，揭示问题的本质；二是希望学生像哲人一样去“推本溯源”，即“刨根问底”。

对于（数学）本原性问题，国内外众多学者早有关注。梳理研究相关文献，发现不少学者是基于学生的认知发展、情感激发等视角来思考本原性问题的。如格兰特·威金斯将基本问题（基本即本原的隐喻）定义为“能激励揭示更多问题，能让学生深入思考与探究，促进思维迈向深入，而不是给出标准答案的问题”［4］。涂荣豹认为，数学本原性问题是站立在教学法基石上，谋略对于师生尤其是学生而言，数学学科主题内最根本、朴素的观点、思想与要领的问题。［5］张荫南认为，数学本原性问题是朴素的、原始的、简单的，能推动数学家创造数学的问题。［6］有些问题是波利亚式的——纯粹数学问题，具有明确的条件与结论，找准解题的策略之后，依靠技巧获得解决。还有一种问题是数学本原问题，关注数学本质，形成数学思想，构建内容体系。我们可以将获得解题规律提升为揭示数学本质，从而学习波利亚，超越波利亚。数学本原问题是数学教学的灵魂，不必包括枝节问题。［7］杨玉东认为，从教学理念上看，数学本原性问题追求的是，从数学学科本身出发，在某个数学主题教学中让学生掌握该主题的数学本质，经历一种类似数学家研究的数学活动过程。这里的“本原性”是教学法意义下的本原性，意味着要考虑对于学生而言，什么是某个数学问题最为根本的、本质的、基本的要素或构成。［8］郑毓信认为，我们不仅应当高度重视“问题引领”，也应当十分重视如何通过相关问题（对此，可统称为“本原性问题”，包括所说的“内容性问题”和“思维性问题”）的再加工，很好地调动学生学习的积极性。［9］李静等认为，本原性数学问题可以从两个层次理解：宏观上，帮助学生比较粗放地认识某个数学主题内容；从微观上，帮助学生精细地研究某个数学核心知识与技能，引导学生理解数学思想与方法。［10］李艳欣认为，本原性问题反映某一学科主题的实质，体现某一数学学习主题最根本的观念、思想和方法。［11］沈威、曹广福认为，数学知识形成的历史背景与数学问题、蕴含的数学思想和应用的科学价值等称为该数学知识的数学本原；数学知识产生的本原情境不一定适合学生，也就需要将数学知识的数学本原与学生的数学现实和生活经验有机结合，重构出能揭示数学本原并适合学生的问题情境；教师引导学生围绕问题情境产生问题，形成概念、原理或理论产生的原始问题，即本原性问题。［12］

虽然国内外众多学者对本原性问题的表述各异，但是对以下四点特征是达成共识的。（1） 本原性问题具有永恒性。主要外化为时空上的生长性和形式上的多样性，在结果上存在多种可能性的问题。例如波利亚“解题表”中的元认知问题：你能否检验这个结果？你能否利用别的方法导出这个结果？你能否把这个结果或方法用于其他的问题？等等。不难发现，这类问题能持续不断地促使学习者反思，并体会使其有可能改变的想法。这类问题表明，教育不仅关注“答案”的学习，还关注如何学习。（2） 本原性问题具有统领性。本原性问题是从教学内容本身所处的知识模块及蕴含的数学思想中提炼出来的，指向一般性观念。一般性观念将零碎知识聚焦整合，使学科不再是一系列支离破碎的概念、规律和方法，它集中展现了学科的结构和本质。例如，在立体几何的判定定理的教学中，“判定定理要研究的问题是什么？”“发现判定定理的思想方法是什么？”等问题，会让学生思考并明确：研究的问题是直线、平面平行或垂直的充分条件，所采用的思想方法是从定义出发探究位置关系所需要的“最少条件”。从这个意义上讲，本原性问题是统摄某一学科或多个学科领域的观念、思想、方法等的集合，是能为话题提供焦点和重要意义的一些具有探究性特质的问题。（3） 本原性问题具有思维性。本原性问题的目的是，通过探究揭示学科的本质，进而促进学生对知识产生和思想方法形成的深入思考。例如，教学“函数y=Asin（ωx+φ）”时，“为什么要学习y=Asin（ωx+φ）？”“如何研究y=Asin（ωx+φ）与y=sin x的关系？”等问题，可以帮助学生通过对具体知识的不断探究以及有序厘清，经历专家思维，最终指向对该问题的深刻理解。（4） 本原性问题具有激励性。本原性问题主要来自教师在备课过程中精心设计的反映该数学主题实质的问题或学生在教学过程中提出的涉及该数学主题实质的关键问题。本原性问题能够最大限度、最大范围地吸引学生参与到问题的探究中，并最终在成功解决时为学生带来巨大的喜悦。例如，教学“等差数列的前n和”时，借助数学史创设情境，使学生提出问题：小高斯是怎么想到那样求和的呢？这个问题不仅指向“探究等差数列前n和的思想方法”的本原，而且极大地吸引着、激发出学生的好奇心，让学生通过基于历史相似性的学习，理解“倒序相加”的本质，即“化不同为相同”“化和为积”和“大道至简”的思想，进而形成进一步探索未知的欲望。

据此，我们将“数学本原性问题”界定为：能激起学生“刨根问底”的探究欲望，并能引领学生探究数学本质内涵的“最根本、朴素的观点、思想与要领”的问题。这里做几点说明：（1） 数学本质的内涵包括“数学知识的内在联系、数学规律的形成过程、数学思想方法的提炼、数学理性精神的体验”等诸多方面。（2） 数学本原性问题可以是数学的问题，也可以是元认知的问题，如波利亚的“你能找一个比它更简单的问题吗？”。（3） 数学本原性问题凸显“刨根问底”的探究精神。例如，“如何得到等比数列前n项和的一般性公式？”这一问题在新授教学中可以作为本原性问题，因为它可以引领学生从最简单的等比数列2n、3n等出发，探究并揭示等比数列前n项和的一般规律和方法产生的过程，同时凸显“刨根问底”的探究精神。但这一问题在复习课中不能作为本原性问题——虽然也能揭示数学的一般规律，但是缺少数学规律的形成过程，不能凸显“刨根问底”的探究精神，更多的可能是记忆。

二、 数学本原性问题提出教学的价值

（一） 培养学生的好奇心和刨根问底的精神

好奇心是探究的原动力。真正的探究者无不是好奇者。受到应试教育的影响，死记结论、重复刷题、硬归题型、套路解题等做法备受推崇，使“成功”的学生产生厌烦情绪，“不成功”的学生产生挫折和痛苦。久而久之，学生成了记忆的容器和做题的机器，失去了学习的兴趣，不再有好奇心。“本原性问题提出教学”主张学生基于情境或问题解决，开展“审视、质疑、比较、分析、判断或决策”等心理活动，进而提出问题或可能成立的结论。其结果并不指向唯一正确的答案，这使学习过程具有悬疑性、探究性。学生在这样的学习活动中会感到很愉快，即产生一种情感上的满足，从而会重新燃起好奇心，萌发提出问题的意愿。“本原性问题提出教学”还主张学生在教师引导下进一步提炼出本原性问题，进而探索关于数学主题的一般性结论和一般性方法。这正是一种追寻数学本质和根源的过程，有助于培养学生刨根问底的精神。

（二） 发展学生的元认知和数学一般性观念

元认知是对学习（认知）过程反思（再认）的过程，包括对学习过程中所有因素的反思（再认）。本原性问题提出是一种反思性学习活动，常常通过“反思—提问—探究—发现—发展—反思—提问……”的循环，借助元认知提问（如波利亚“解题表”中的元认知问题）来提出本原性问题，从而为学生的自主探究做好导向。数学一般性观念是数学大概念的一种表现形式，是对数学内容及其反映的数学思想和方法的进一步提炼和概括，是对数学对象的定义方式以及几何性质指什么、代数性质指什么、函数性质指什么、概率性质指什么等问题的一般性回答，是研究数学对象的方法论，对学生学会用数学的方式观察、思考事物以及发现、提出数学问题等都具有指路明灯的作用。［13］提出本原性问题要基于知识发展和认知过程的合理性，从学习内容所处的知识模块和所含的数学思想中提炼一般性观念——这离不开教师对学生的引导。由此，学生可以通过派生性问题（链）展开具体探究，从而不断完善认知结构，体悟学习内容是什么、为什么、怎么学——这一过程又可以发展一般性观念。

（三） 提升学生的创新意识和理性精神

基础教育追求高质量发展，国家需要拔尖创新人才。丘成桐先生说过：创新的基础在质疑问难。［14］实际上，“大部分的伟大发现（发明）都应归功于问号”。好奇心不仅是探究的原动力，而且是创新的支撑点。而“本原性问题提出教学”不仅具有悬疑性基础上的探究性，而且具有创造性，能够提升学生的创新意识。数学是思维的科学，数学思维更多的是一种理性思维。“本原性问题提出教学”不仅鼓励学生质疑问难（提出问题），激活思维，而且引导学生刨根问底（提出本原性问题），这是严谨求实的理性精神的重要表现。

三、 数学本原性问题提出教学的路径

下面以“二面角”为例，说明开展数学本原性问题提出教学的基本路径。

（一） 明确数学本原性问题

要引导学生提出本原性问题，教师首先要明确本原性问题，这很考验教师对学科的理解。根据数学本原性问题的内涵与特征，教师需要在数学知识的联系与结构、知识背后的思想与精神以及知识形成的过程、思维发展的脉络中寻找教学内容的本质与源头，从而明确数学本原性问题。为此，尤其要重视对教学内容的逻辑（体系）分析和历史（过程）分析。

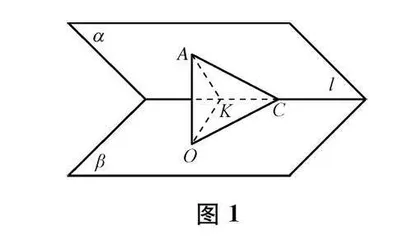
“二面角”是苏教版高中数学必修第二册“13.2.4 平面与平面的位置关系”第2点“两平面垂直”中的铺垫性内容（为引出两平面垂直的定义做铺垫）。从逻辑体系的角度看，二面角是两平面位置关系的一般性表征，两平面垂直是它的特殊情况（二面角的大小为90°），两平面平行可以看作它的极端情况（二面角的大小为0）；二面角是线线角、线面角的升维推广，完善了空间角的概念；将二面角转化为线面角进而转化为线线角来度量大小体现了降维的思想，二面角与其平面角（线线角）之间的对应关系架起了平面几何与立体几何之间的桥梁。从历史的角度看，二面角概念起源于19世纪初数学家高斯对天体运动的研究，是为了以精确度量的方式来研究两个平面的位置关系，之后广泛应用于立体几何的相关领域。

由此，可以确定“二面角”内容的两个本原性问题：（1） 相关的现实情况有怎样的数学特征，可以用怎样的数学概念来表示？（2） 二面角有什么作用，如何精确刻画两个半平面的位置关系？其中，前者指向二面角定义的形成，而后者指向二面角大小的度量。并且，大小比定义更重要，更能反映二面角的本质。这一点与平面角（线线角）是一致的。［15］

（二） 引导学生提出数学本原性问题

如何引导学生提出本原性问题？这很考验教师对学生的理解及教学的技艺。笔者认为，首先需要创设蕴含本原性问题的情境（包括“现实的、科技的、数学的”情境），激发学生的好奇心，让学生用数学的眼光观察、搜寻、辨析、识别情境中的各种信息，剔除干扰信息和次要信息，确定有效信息和重要信息，形成提出问题的线索（如矛盾、联系等），然后依据自己的理解表征这些线索，提出有关问题。在此基础上，可以通过一些提示语，引导学生关注最为根本（一般）和朴素（原始）的线索与内涵，提出本原性问题；也可根据学生提出的多个问题，引导学生评价、取舍、修正、完善、归类、排序、提炼、溯源，从而确定本原性问题。