中学数学教材中圆周率内容的教育价值与教学建议*

摘要：现行初高中数学教材中的圆周率内容主要有刘徽“割圆术”、布丰投针试验、圆周率的估算以及圆面积和周长的计算等，分布在多个知识领域（主题），主要分布在阅读材料和习题中。这些内容蕴含极限和递推思想、统计与概率思想、微分思想、求实精神、创新精神、统一美、简洁美、奇异美等。教学时要注意：梳理数学发展脉络，让整体感知与深度探究相结合；开展数学主题教学，让横向联系与纵向贯通相结合；优化内容表征形式，让显性呈现与隐性渗透相结合。

关键词：中学数学；圆周率；教育价值；数学史；主题教学

圆周率（圆的周长与直径之比）是数学中最重要的一个常数，与数学多个分支中的众多内容有着丰富的联系。人类对圆周率的认识与探索，有着悠久的历史和漫长的过程，积淀了厚重的数学文化。学生在小学高年级的数学学习中初步认识了圆周率后，在中学的数学学习中还会进一步认识圆周率。本文尝试在梳理现行初高中数学教材中圆周率内容的基础上，剖析其教育价值，给出相应的教学建议，供中学数学教学参考。

一、 中学数学教材中的圆周率内容

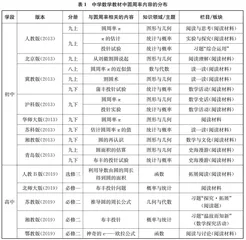
现行初高中数学教材中圆周率内容的分布如下页表1所示。由此可知，圆周率内容主要有刘徽“割圆术”、布丰投针试验、圆周率的估算以及圆面积和周长的计算等，分布在图形与几何、几何与代数、数与代数、函数以及统计与概率等知识领域（主题），具体涉及正多边形和圆、弧长和扇形面积、空间图形的表面积和体积、实数、求导法则及其应用以及用频率估计概率、事件的概率等知识内容；同时，主要分布在阅读材料性质的栏目中，少数分布在习题性质的板块中。

二、 圆周率内容的教育价值

（一） 思想价值

1. 蕴含极限和递推思想

多版教材都以阅读材料的形式介绍圆周率，阐述圆周率估算的发展过程。其中，刘徽创立的“割圆术”是非常重要的方法，蕴含了深刻的数学思想，可归结为两个方面：

一是极限思想。“割圆术”用圆内接正多边形的面积来逼近圆的面积（如图1所示），从而计算圆周率的近似值。其中，蕴含了化归（化圆为方）和极限（不断逼近）的思想。相对而言，极限思想在中学数学内容中体现得比较少。其实，极限是数学的重要思想。在中学教学中渗透极限思想，能充分拓展学生的想象空间，让学生体会有限与无限的意义及转化，在有限中认知无限，从而认识量变到质变的过程，感受数学的严谨性。

……

二是递推思想。刘徽从圆的内接正六边形出发，对每边做二分，以此计算正多边形的面积。如图2所示，设圆的半径r=1，AB、AC分别为圆内接正n边形和正2n边形的边长，且AB=an，AC=a2n，则AP

=12an，PC=1-OP=1-1-14a2n，a2n=AP2+PC2=2-4-a2n，最终求得面积S2n=12nan（n=3×2m，m=1，2，3，…）。

可见，圆内接正多边形的面积是借助边长的递推公式获得的，这体现了递推的思想。

因此，不必计算每个正多边形的面积，这显著地加快了正多边形面积对圆面积的逼近速度。理论上，利用“割圆术”能将π的近似值计算到任意精度。

2. 蕴含统计与概率思想

在圆周率估算的发展过程中，数学家还创造性地采用了统计与概率的方法。其中，“布丰投针试验”是用几何形式表达概率问题的首例，开创了用随机数据处理确定性数学问题的方法。该试验实际上是求投针与平行线相交的概率。如图3所示，在画有间距为a的两条平行线的白纸上随意扔一根长度为l（l<a）的针，记落下后针的中点为M，M与最近的平行线距离为x，针与此线的夹角为φ，则0≤x≤a2，0≤φ<π。要使针与此线相交，需要x≤l2sin φ。作出x与φ关系的图像，如图4所示。利用几何概型概率计算公式，可以求得概率p=2aπ∫π0l2sin φdφ=2lπa。由此可以推出π=2lpa。那么，当两条平行线的间距a和针的长度l确定后，只要利用频率估计概率，就可估算出π的值。在试验过程中，学生能感受到频率的稳定性：随着试验次数增多，频率在概率附近摆动的幅度会减小。

此外，人教版和苏科版初中数学教材还介绍了一种新的求π近似值的方法：如图5所示，随机撒一把米在画有一个正方形及其内切圆的白纸上，统计落在圆内的米粒数m和落在正方形内的米粒数n，计算频率mn从而估算π的值。这种方法也体现了统计与概率的思想。

3. 蕴含微分思想

人教B版高中数学教材中的一个阅读材料，介绍了“利用导数由圆的周长得到圆的面积”的方法。如图6所示，设半径为r时圆的面积为S，半径增加Δr时圆的面积增加ΔS。当Δr足够小时，ΔS近似地等于长2πr、宽Δr的矩形的面积，即ΔS≈2πrΔr，故ΔSΔr≈2πr。令Δr→0，可得S′=2πr。又（πr2）′=2πr，可得S=πr2。这个方法揭示了圆的周长和圆的面积的实质性联系。它实质上是微元法，即取对象的微小变量来处理；蕴含着微分的思想，能有效解决曲线问题（化曲为直）。

（二） 精神价值

1. 蕴含求实精神

圆周率估算的发展过程（如下页图7所示）

凝聚了数学家的求真务实精神。从我国现存最早的数学典籍《周髀算经》记载的“周三径一”到古希腊托勒密的改进；之后刘徽创立“割圆术”，最初算到192边形，得到近似值3.14，认为不够精确，最终算到3072边形，得到近似值3.1416；祖冲之继续运用“割圆术”，更是求得3.1415926<π<3.1415927，并得到两个近似分数，即约率227和密率355113；再后随着数学的发展，π的估算越来越精确。可以说，正是由于数学家的求真务实精神，才有了璀璨的数学文化。

2. 蕴含创新精神

数学是一门富有创造性的学科。数学家通过发现新的数学定理和解决复杂的数学问题，展示人类的创新能力。圆周率估算的发展过程可以分为四个时期。实验法时期，人们凭借生活经验，发现圆的周长总是其直径的3倍多。几何法时期，阿基米德利用内接正多边形与外切正多边形“内外相夹逼近”计算圆周长，从而获得圆周率；刘徽首创“割圆术”，将圆与正多边形结合起来，用直线解决曲线问题，揭开了无限世界的神秘面纱；祖冲之在此基础上计算到小数点后7位。分析法时期，数学家用微积分方法把圆周率表示成无穷级数、无穷乘积、连分数的形式，进而计算圆周率。计算机的出现使圆周率的计算进入新阶段，成为检验计算机精确性和可靠性的手段。追溯这一发展过程，可以发现，每一次突破都经历了思维的创新。

（三） 美学价值

1. 蕴含统一美

自然界原本就是统一的。无论怎么画圆，圆的周长与直径的比不变，统一于π；π是无限不循环小数，数值在不断延伸，却又永远无法被完全表示。欧拉公式eiπ+1=0将数学中看起来不相关的重要常数（自然对数的底、虚数单位、圆周率以及1、0）统一起来，同时将指数函数的定义域扩大到复数域，建立了三角函数和指数函数的联系，被誉为“数学中的天桥”。数学中这种完美的统一激发了人类思维的极限。

2. 蕴含简洁美

圆周率计算方法的不断优化，充分体现了对简洁美的追求，例如递推方法的引入。此外，在不断探索中，人们认识到圆周率是无限不循环小数。然而，在用符号π专门表示之前，其名称和数值都没有统一，表示和计算显得异常烦琐；不同时期所选的符号及表示的含义也不尽相同，很不利于国际交流。1706年，英国数学家威廉·琼斯首先使用符号π表示圆周率。［1］之后，在欧拉的倡导下，π成为国际通用符号。圆周率符号的确立，使圆的周长和面积公式有了更简洁的表达方式。

3. 蕴含奇异美

圆周率计算方法（表示方式）的不断更新，还充分体现了数学的奇异美，激发着人们的探索欲，使人们对圆的性质有了更深的认识。除了各种无穷的表达式，最典型的莫过于统计与概率方法。相传，布丰曾拿出一张预先画有多条等距离平行线的纸，抓起一大把长度是平行线间隔一半的小针，邀请客人把这些小针一根一根地往纸上投，并记录小针与平行线相交的次数。最后，他宣布：“共记录投针2212次，其中与平行线相交704次。2212与704的比值3.142是圆周率π的近似值！”客人无不感到不可思议而大声赞叹。

三、 圆周率内容的教学建议

（一） 梳理数学发展脉络，让整体感知与重点探究相结合

教材中的圆周率内容比较分散，不利于学生理解，尤其是不利于学生感悟其中的思想价值、精神价值和美学价值。因此，教师要系统地梳理圆周率知识的发展脉络（如图8所示），引导学生在整体感知的基础上，有重点地进行深度探究。整体感知，主要是高效地再现或重构历史，让学生经历类似的探究过程，感受知识产生与发展的自然性和必要性。重点探究，主要是充分地挖掘教材中的相关内容，发挥不同版本教材的编写优势，必要时借助课外书籍、信息技术等进行拓展和优化，从而加深学生对重点内容的理解和感悟。

（二） 开展数学主题教学，让横向联系与纵向贯通相结合

教材中的圆周率内容主要分布在阅读材料和习题中，与主干知识联系较弱。这常导致教师在教学中对圆周率内容不够重视或“虽然重视，但是不会使用” ［2］。对此，教师可从主题教学的角度统整教学内容，融合主干知识与拓展内容，从而既注重横向联系，也强调纵向贯通。具体地，可以采取多种整合方式，如：从古到今，追寻圆周率知识的发展过程；从现实、熟悉的问题出发，回溯发展过程中的重要人物与事件；以关键人物或事件为线索，分析相关数学概念以及数学思想的演变。［3］例如，以“圆的面积”为主题展开教学：如下页图9所示，从割补法入手，整体感知化归思想；介绍刘徽的“割圆术”，在递推求面积

以及圆周率的计算中感受数学的严谨，渗透极限

的思想；类比推导圆的面积公式和扇形面积公式；利用导数求圆的周长和面积，感悟微分的思想，运用于球的表面积和体积公式推导［4］。

（三） 优化内容表征形式，让显性呈现与隐性渗透相结合

教材中的圆周率内容主要以文字形式出现（附少量图片），不利于学生理解内容（知识），感悟价值（文化）。文化价值具有内隐的特征，需要渗透在外显的知识内容中。教学中，教师要对知识内容进行优化表征和裁剪重组，以更具有情境性和问题性、更生动和活泼的形式呈现，与学生的认知基础和思维特点相契合，让学生在学习活动中体悟文化价值。例如，冀教版初中数学教材中的“投针试验”内容以数学文化为背景，对原有情境进行改编，可操作性较强。在教学过程中，可以创设问题情境引发学生深度思考：为什么要设置间隔相等的平行线？如何提高π估算的精度？在分析环节，要与其他“π的估计”试验对比，借助几何画板动态呈现频率与概率的关系（如图10所示），从而促进学生深度理解与感悟。

参考文献：

［1］ F.Cajori.A History of Mathematical Notations：Vol.2［M］.La Salle：The Open Court Publishing Company，1951：913．

［2］ 罗圣洁，杨新荣.2019版高中数学必修教材的中国元素比较研究——以人教A版、北师大版、苏教版和湘教版为例［J］.中学数学月刊，2023（1）：4046.

［3］ 李明振，庞坤.数学史融入中学数学教材的原则方式与问题［J］.数学通报，2006（3）：2325.

［4］ 李习凡，朱胜强.类比思想引路，数学软件辅助——“球的表面积和体积公式”的探究教学［J］.教育研究与评论（中学教育教学），2021（8）：9092.