一道平面几何新定义试题的命制思考

摘要：2021年苏州工业园区中考一模第 28题是一道平面几何新定义问题 ，分三个层次设计 ，考查相似三角形、黄金分割点、圆的有关性质、锐角三角函数等知识 ，以及综合运用数学知识、思想方法探索规律、解决问题的能力。本题的命制从初始问题出发 ，在分析解答的基础上 ，通过对 “相似分割线 ”这个新定义的理解 ，运用静态与动态两种图形研究方法 ，对两个关联的三角形中不变的结论和变化的规律进行了深入的研究 ，进而居高临下 ，考虑学情 ，推敲细节，打磨成稿。

关键词 ：数学中考 ;试题命制 ;平面几何 ;新定义 ;相似分割线

一、试题及评析

2021年苏州工业园区中考一模第 28题如下 ：

【理解概念】

分别经过两个不相似的直角三角形的直角顶点的两条直线 ，分别把这两个直角三角形分成两个小三角形 ，当一个直角三角形中的一个小三角形与另一个直角三角形中的一个小三角形相似时 ，另外两个小三角形也相似，则称这样的两条直线叫作这两个直角三

角形的相似分割线 。【巩固新知】

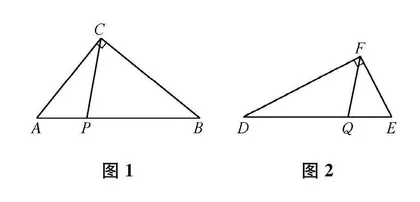
（1）如图 1、图 2，在 △ABC和 △DEF中，∠ACB =∠DFE =90°，∠ACP =∠D， ∠DFQ=∠A。

①求证 ：CP、FQ分别是 △ABC和

△DEF的相似分割线 ;

②若 AC=6，BC=8，DF=8，EF=4，求

AP的长。【拓展提高】

（2）如图 3，AB为 ☉O的直径 ，点 C、D在☉O上，CP、DQ分别是 △ABC和 △ABD的相似分割线 ，且△ACP∽△DAQ。

①若点 P是AB的黄金分割点 ，则点 Q是否也是 AB的黄金分割点 ？说明理由 ;

②若∠ABC=30°，AC=2。当 CP⊥DQ时，试在图 4中画出 △ABD及CP、DQ的大致位置 ，并直接写出 AP的长。

本题是一道平面几何新定义问题 ，分三个层次设计 ：第一层次是 “相似分割线 ”概念的理解 ;第二层次是在概念理解的基础上静态探究结论 ，并实际操作计算 ;第三层次是在静态探究的基础上动态探究规律 ，并利用规律解决问题。引导学生探究隐藏在两个关联的三角形中不变的结论和变化的规律 ，考查学生对相似三角形、黄金分割点、圆的有关性质、锐角三角函数等知识的掌握情况 ，以及综合运用数学知识、思想方法探索规律、解决问题的能力 ，能够让不同水平的学生充分展示自己的探究水平 ，有良好的效度和区分度。

二、命题缘起

“三角形 ”“四边形 ”和“圆”是初中平面几何的核心知识板块 ，自然也是重要考查内容。以往的考查 ，多是在一个图形内部的考查 ，而不是对两个图形之间联系的考查 ;多是静态或动态的考查 ，而不是动态与静态相结合的考查。同时 ，主要是以三角形或四边形为载体产生图形的变化 ，而很少与圆相结合 ，以圆为背景形成图形的变化。

强化 “核心素养导向 ”是数学试题命制的出发点和落脚点。为此 ，需要关注数学本质 ，关注通性通法 ，综合考查 “三会 ”统领下的 “四基”与“四能 ”。新定义试题是以 “新知 ”为载体，突出考查学生综合运用所学知识与思想方法在新情境下分析、解决问题的能力 ，通常没有固定的解法 “套路 ”与 “技巧 ”，可以有效地考查学生的 “真知识 ”“真思维 ”“真能力 ”。此外 ，解答题形式的新定义试题一般由 “文本理解 ”“新知内化 ”“灵活应用 ”这三个由浅入深的部分构成 ，这和 “三会 ”的理念具有高度的一致性。

由此 ，命题组决定 ，命制一道与上述核心知识有关的平面几何新定义试题 ，作为整卷的压轴题。

三、命题过程

（一）初始问题的选取及分析

我们选取的作为命题素材的初始问题如下 ：

在两个不相似的直角三角形中 ，分别存在经过直角顶点的一条直线 ，把直角三角形分成两个小三角形后 ，如果第一个直角三角形分割出来的一个小三角形与第二个直角三角形分割出来的一个小三角形相似 ，那么分割出来的另外两个小三角形也相似。把这样的两条直线称为这两个直角三角形的相似分 割线 。

如下页图 5、图 6，直线 CG、DH分别是两个不相似的 Rt△ABC和 Rt△DEF的相似分割线 ，CG、DH分别与斜边 AB、EF交于点

G、H，如果 △BCG与 △DFH相似 ，并且 AC =3，AB =5，DE =4，DF =8，那么 AG =。

“相似分割线 ”这个新定义简单明了 ，它建立了两个直角三角线被分割成的两组三角形（存在两组内角互余、一组内角互补的关系）之间的相似关系。

解决这个问题之前 ，先要明确 ：当△BCG ∽△DFH时，另外两个三角形 ，即△ACG和

△DEH是怎么对应相似的 ？有没有多种对应方式 ？由 △BCG∽△DFH可得 ∠BCG= ∠F，∠B =∠FDH，由互余关系不难得到 ∠ACG=∠E，∠A=∠EDH，所以 △ACG∽

△DEH。由此可见 ，当给出 △BCG∽△DFH时，另一组对应关系也唯一确定。

由上述过程可得 ，当 △BCG ∽△DFH时，CG、DH分别是两个直角三角形的相似分割线。而若 ∠BCG=∠F，∠B=∠FDH，则

△BCG∽△DFH。故可以得到相似分割线的构造方法 ：过点 C作 CG，使得 ∠BCG= ∠F，过点 D作 DH，使得 ∠FDH =∠B，则直线 CG、DH分别是两个直角三角形的相似分割线。由此可以得到结论 ：任意两个不相似的直角三角形一定分别存在相似分割线。

明确了 “相似分割线 ”背景下三角形相似的对应关系 ，以及 “相似分割线 ”的构造方法 （存在性 ）之后 ，利用两组三角形之间的相似关系 ，不难解决本题 ：

因为 ∠ACB=90°，AC=3，AB=5，所以 BC=4。根据题意可得 △ACG ∽△DEH， AG AC 3 BG

△BCG∽△DFH，所以 DH =DE =4，DH

BC 4

=DF =8。设 AG=3x，则 DH =4x，BG=

2x。由 AG+BG=AB，可得 3x+2x=5，解得x=1，所以 AG=3。

可见 ，本题以 “相似分割线 ”为背景考查这个新定义表层的特征 ，解题时只是简单地用到了三角形相似。

（二）对“新定义 ”的深入研究命题组感觉到 “相似分割线 ”这个新定义有着丰富的内涵 ，便对其进行了深入研究。

1.静态研究

静态研究指在静止状态下研究图形 ，一是对图形相关要素的研究 ;二是通过某些特殊的方法构造出新图形及新要素 ，对构造出的图形及要素进行研究。这是图形研究的基本方法。

先研究 AG 的值。解答初始问题的过程

BG

给人一种微妙的感觉 ：AG 的值很特殊 ，决定

BG

了分割成的两个三角形 （实际上决定了点 G的位置 ，也就决定了分割线 CG的位置 ），而且由最初两个不相似的直角三角形的形状确定。考虑一般情况 ，不妨设 Rt△ABC和 Rt△DEF中，CA=a，CB=b，DE=c，DF= d，由△ACG∽△DEH，△BCG∽△DFH，可AG AC aBG BC b AG

得DH =DE =c ，DH =DF =d ，所以 GB =

ad

bc，为定值。

FH FH

再研究 EH的值。类比猜想 EH的值也

AG

很特殊 ，大胆猜测其和 BG的值相等。证明方

法还是利用 △ACG ∽△DEH，△BCG ∽

△DFH，一是得到 CG AC =a ，CG BC

EH =DE cFH =DF b FH ad CG AG

=d ，所以 EH =bc;二是得到 EH =DH ，

CG BG 所以 FH AG 。

FH =DH ，EH =BG

在此基础上重新构图。点 G和点 H在相应斜边上的位置关系是对应的 （分相应斜边所成的比相等）。比如 ，若 G是线段 AB的黄金分割点 ，则 H是线段 FE的黄金分割点。那么 ，当两个斜边一样长时 ，它们被分成的两组线段对应相等。即当 AB=FE时，AG= FH，BG=EH。由此 ，命题组进行了简化图形的尝试 ：如图 7，设计两个共斜边的不相似 （也就是不全等 ）的直角三角形 ，以及它们的相似分割线。显然 ，在图 7中，由 △ACP ∽

△DAQ，△BCP∽△DBQ，有 AP=BQ。

2.动态研究

动态研究指在运动状态下研究图形 ，从而更好地揭示图形变化中蕴含的不变性 ，并且探究图形变化的一些其他规律。这是图形研究的重要方法。

为了更好地探究图 7中图形的内在联系，可以改变两个直角三角形的形状。由两个直角三角形有公共的斜边 ，不难想到可以将它们放入同一个圆中 ：以 AB的中点 O为圆心、AB为直径作圆 ，则点 C、D在圆 O上。此时 ，不仅有 AP=BQ，而且有 OP=OQ。

在此基础上 ，命题组利用 “几何画板 ”软件进一步探索变化规律 ，发现 ：

（1）点 C、D在线段 AB的同侧时 ，由角相等易得 CP∥DQ。利用圆的对称性 ，可以重新思考相似分割线的构造方法 ：如图 8，作直径 DD'（找点 D关于圆心 O的对称点 D'），连接 CD'交AB于点 P，作直径 CC'（找点 C关于圆心 O的对称点 C'），连接 DC'交AB于点 Q，则CP、DQ分别是两个直角三角形的相似分割线。证明只要利用 “同弧所对的圆周角等于圆心角的一半 ”和“对顶角相等 ”，得到

11

∠BCP=2∠BOD'=2∠DOA =∠DBQ，

11

∠BDQ=2∠BOC'=2∠COA=∠CBP。

由此做进一步探索 ：如图 9，延长 DQ交圆 O于点 E，连接 EB，则由 △ACP ∽

△DAQ，可得 ∠ACP =∠DAQ，∠CAP = ∠ADQ，由同弧所对的圆周角相等 ，可得 ∠DAQ =∠BEQ，∠ADQ =∠EBQ，所以 ∠ACP=∠BEQ，∠CAP=∠EBQ，又由 AP =BQ，可得 △ACP≌△BEQ。

（2）点

C、D在线段 AB的异侧时 ，直线 CP与 DQ相交。由角相等可以发现其中的对称性 ：如下页图 10，设 CP与DQ相交于点 E，由 △ACP ∽△DAQ，可得 ∠CPA = ∠AQD，所以 ∠QPE=∠PQE，从而 PE=QE，即△PQE是等腰三角形 ，故点 E在线段 PQ （或直径 AB）的垂直平分线上 ，即在过点 O且垂直于 PQ（或 AB）的直线上运动。通过 “几何画板 ”软件的操作 ，可得点 E的运动轨迹为射线FO。

此时做进一步探索 ，可得相似分割线新的构造方法 ：如图 11，过点 D作平行于直径 AB的弦 DD'（找点 D关于直径 AB中垂线的对称点 D'），连接 CD'交AB于点 P，过点 C作平行于直径 AB的弦 CC'（找点 C关于直径 AB中垂线的对称点 C'），连接 DC'交 AB于点 Q，则CP、DQ分别是两个直角三角形的相似分割线。利用等弧所对的圆周角相等 ，容易证明这个构造方法等价于之前作角相等的构造方法。

（三）试题成稿

将“相似分割线 ”概念的有关性质 （及判定）研究透了 ，命制试题便可居高临下 ，重在考虑学情 ，推敲细节 ，打磨成稿。