数学提问能力评价框架研究

摘要：在正规考试中加强提问能力的评价，有利于“以评促教”，切实培养学生的提问能力。在借鉴已有的一些研究的基础上，建构了以流畅性、灵活性、新颖性、深刻性、清晰性为评价维度的数学提问能力的评价框架，并就各维度水平的划分、权重的确定以及试卷评阅中的操作实施提出了具体建议。

关键词：提问能力;提出问题;数学问题;评价框架;考试

江苏第二师范学院和南京师范大学联合培养的硕士研究生。《义务教育数学课程标准（2011年版）》和《普通高中数学课程标准（2017年版2020年修订）》都十分强调培养学生从数学的角度提出问题的能力。为了更好地培养学生的数学提问能力，需要科学地评价学生的数学提问能力。

本文通讯作者。关于数学提问能力的评价，国内外学者已经进行了一些有益的探索，但相对于日常教学中的形成性评价，正规的考试，尤其是中、高考等大规模、高利害的考试，特别需要关注评价标准的确定性、标准执行的程序性、评阅工作量的可控性等，命题、阅卷人员都希望有一个相对程序化的实施建议。为此，本文在借鉴已有的一些研究的基础上，尝试建构数学提问能力的评价框架（指标体系），并且对正规考试中数学提问能力的评价给出一些操作性建议。当然，这样的框架对日常教学中的形成性评价也有借鉴价值——日常教学中，还可以评价学生数学提问的过程以及学生在数学提问过程中的情感态度等。

一、评价维度的建构

对提问能力的评价，较早的评价方法源于托伦斯的创造性思维测验（1966）。在早期的研究中，有研究者在该测验的启发下，提出了从流畅性、灵活性、独创性三个维度评价提问能力。Lyn D.English.Childrens Problem Posing within Formal and Informal Contexts[J]. Journal for Research in Mathematics Education，1998 （1）： 83106。夏小刚等人借鉴托伦斯的做法，以问题的数量、问题的种类和问题的新颖性为指标，建立了一个关于数学提问能力的评价标准。夏小刚，汪秉彝，吕传汉.中小学生提出数学问题能力的评价再探[J].数学教育学报，2008（2）：811。Silver和Cai从以下三个维度评价学生的数学提问能力：（1）问题的数量;（2）新颖性;（3）复杂性。E.A.Silver， J.Cai.Assessing students’ mathematical：problems posing[J].Teaching Children Mathematics， 2005（12）：129135。陈丽敏等人则综合上述研究，从流畅性、变通性、新颖性、复杂性四个维度评价学生的数学提问能力，其中的复杂性是指提出的正确的数学问题所包含的语义类型的个数。陈丽敏，景敏，Verschaffel Lieven，等.五年级小学生数学问题提出能力和观念的调查研究[J].数学教育学报，2013（2）：2732。洪丽暖和郭玉峰选用了流畅性、灵活性、深刻性三个评价维度。洪丽暖，郭玉峰.初中生数学问题提出能力的年级差异研究[J].中国数学教育，2019（23）：311。李欣莲和蔡金法在评价基于现实的数学提问能力时选用了灵活性、新颖性、深刻性、适切性四个维度。李欣莲，蔡金法.数学课堂中学生问题提出的评估[J].小学教学（数学版），2020（6）：2226。

上述研究的评价维度中多包括流畅性。流畅性评价的是学生能否流畅地提出数学问题，在一定程度上反映了学生的数学提问能力，因此是评价学生数学提问能力的基本指标。流畅性可以通过学生提出数学问题的数量来反映。当然，这里的数学问题应该是有效的，即可以让人理解的、具有实际意义的问题。

提问能力强的人，不仅能提出更多数量的问题，而且善于从不同的角度提出不同类型的问题。因此，评价学生的数学提问能力，还应关注学生能否从不同的角度提出不同类型的问题，也就是上述研究中提到的灵活性或变通性。我们更倾向于使用“灵活性”。灵活性考查的是学生能否灵活地提出不同种类的问题，通过提出的有效问题的种类来反映。当然，这就涉及对所提问题的分类。一般而言，一个有效的问题涉及有关信息以及有关信息之间关系的表达，因此，可以从信息来源、表达形式两个角度对有效问题进行分类。从信息来源看，主要有两类：信息来源于已知情境的数学问题，可称为非拓展性问题;信息超出了已知情境的数学问题，包括改变已有信息或增加额外信息而提出的问题，也包括拓展已有情境而提出的问题，可称为拓展性问题。表达形式是指数学问题的表达形式，如“……比……多多少本”与“……与……之和”是两种不同的问题表达形式。当然，分类有“粗细”之别。对学生提出的问题进行分类，难免存在一些争议。所幸的是，正规考试中，一般都会在正式阅卷前抽取一定数量的试卷进行试阅，在试阅阶段，阅卷组可以针对学生提出的问题进行集体研讨，确定出合理的分类并给出每一类问题的典型案例，进而制订出细化的阅卷标准，便于正式阅卷时对照。

提问能力强的人，还善于提出新颖的问题。事实上，相对于常规的问题，科技进步更大程度上依赖于新颖问题的提出。这也是很多学者将新颖性或独创性作为评价学生数学提问能力的一个维度的重要原因。我们更倾向于使用“新颖性”。新颖性考查学生能否提出与众不同的问题，通过提出的新颖问题的数量来反映。按照托伦斯创造性思维测验的基本思想：“独创性的分数是由统计频数决定的。如果被试的想法或观点罕见于常模所记录的学生的想法，就可以认为这种想法具有独创性。”A.J.斯塔科.创造能力教与学（第二版）[M].刘晓陵，曾守锤，译.上海：华东师范大学出版社，2003：303。因此，对于一道具体的测试题，可在对一定规模的学生进行测试后，确定学生提出的常规性问题（即常模问题）。但多数测试题缺少类似的测试数据作为基础，此时可以观察本次测试中所有学生提出的问题，将其中占比较小的问题视为新颖性问题。

《义务教育数学课程标准（2011年版）解读》指出：发现问题是经过多方面、多角度的数学思维，从表面上看起来没有关系的一些现象中找到数量或空间方面的某些联系，或找到数量或空间方面的某些矛盾，并把这些联系或矛盾提炼出来;提出问题是在已经发现问题的基础上，把找到的联系或矛盾用数学语言、数学符号集中地以“问题”的形式表述出来。教育部基础教育课程教材专家工作委员会.义务教育数学课程标准（2011年版）解读[M].北京：北京师范大学出版社，2012：124。从看似没有关系的现象中找出数量或空间方面的联系考验学生思维的深刻性，因此，深刻性也应成为评价学生数学提问能力的一个重要指标。在上述研究中，多用“复杂性”。比如，陈丽敏等人以提出的问题中语义类型的多少来刻画问题的复杂性;Silver和Cai则认为，复杂性包括语言复杂性和数学复杂性。李欣莲和蔡金法虽然使用了深刻性这一评价维度，但其深刻性指解决所提问题所需的思维深度，可以常规解答所需的基本步骤为指标，步骤越多，说明难度越大，所代表的深刻性也越强。李欣莲，蔡金法.数学课堂中学生问题提出的评估[J].小学教学（数学版），2020（6）：2226。洪丽暖和郭玉峰所说的深刻性最终也用所提问题的难度来刻画。洪丽暖，郭玉峰.初中生数学问题提出能力的年级差异研究[J].中国数学教育，2019（23）：311。也就是说，上述研究中的“深刻性”还是表现为所提问题的复杂程度。但考查学生的数学提问能力时，学生更多地思考某个背景中有哪些数学问题，而较少思考某个数学问题的复杂程度、难易程度等。另外，我们希望引领学生提出更多的数学问题，也不建议以数学问题的复杂程度、难易程度来干扰学生提出数学问题的过程;语言的复杂性或者语义类型的多少，可能在一定程度上反映了所提问题的复杂程度，进而也在一定程度上反映了所提问题的深刻程度，但两者并不完全等同。因此，上述研究具有一定的借鉴价值，但并不能直接反映所提问题的深刻性。反映所提问题的深刻性，应该以问题与原有背景之间的关联为基础，而不应以问题的外在描述形式为依据。提出问题，自然需要基于原有背景中的信息，因此，所提问题涉及背景中信息量的多少以及这些信息之间的相互交织程度，可以较好地反映所提问题的深刻性。能够基于纷繁复杂的信息和信息关系提出问题，可以反映学生思维的深刻性。因此，我们以问题所含信息的数量以及信息之间的联系程度来刻画问题的深刻性。

另外，发现问题和提出问题两者尚存在一定的区别，前者更多地关注能发现具体情境中的问题，但发现了问题之后，还需要能清晰地表述出来，因此，评价学生的数学提问能力时，同样应关注学生所提问题的清晰程度，即清晰性也是考查学生数学提问能力的一项重要指标。清晰性是指学生提出有效问题时语言表达的清晰程度（无效问题直接判定不给分，无须分析其清晰性）。

至于适切性，是指提出的问题应符合实际，符合常识。李欣莲，蔡金法.数学课堂中学生问题提出的评估[J].小学教学（数学版），2020（6）：2226。实际上，就是要求提出的问题是有效的数学问题。前文在“流畅性”中已经指出了这一点，因此，适切性不能成为一个独立的评价维度。

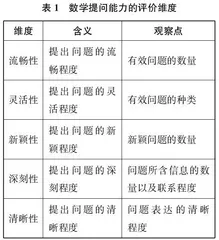
综上，我们选取流畅性、灵活性、新颖性、深刻性、清晰性五个维度（详见表1），来建立数学提问能力的评价框架。

二、各维度水平的划分

为了直观地表示学生的数学提问能力，在确定数学提问能力的评价维度的基础上，自然需要进一步划分各维度的水平，形成计分方法。

关于计分方法，上述研究都采用了简单叠加法。比如，陈丽敏等人的研究中，流畅性维度的计分方法是，学生提出了几个正确的数学问题，则得几分;变通性维度的计分方法是，学生提出了几类数学问题，则得几分;新颖性维度的计分方法是，学生每提出一个新颖的数学问题，则得1分;复杂性维度的计分方法是，学生提出的数学问题中包含两种语义类型则得1分，包含3种及以上语义类型则得2分，其余为0分;最后将四个维度的得分相加，就得到学生该测试题的分值。陈丽敏，景敏，Verschaffel Lieven，等.五年级小学生数学问题提出能力和观念的调查研究[J].数学教育学报，2013（2）：2732。这种方法操作简便，但存在这样两个方面的问题：

一是分值简单叠加不科学。比如，面对一道测试题，提出6个同类问题的甲学生与提出分别属于3类的4个问题的乙学生，从流畅性维度和变通性维度看，得分相同（分别为6+1和4+3），这显然不甚合理。

二是各维度得分区间差异大且不可控。上述得分规则下，流畅性维度、变通性维度、新颖性维度得分区间差异很大，其中新颖性维度得分区间极小;而所提的各问题分别赋分后再相加，导致复杂性维度得分占比过高。

对此，建议统一以各维度的达成度（指该维度实际的达成状况与预设的满分状况的比值）作为该维度的得分依据。以达成度作为评价标准，首先，具有简单、明确等优点刘春惠.泰勒课程评价模式述评[J].北京邮电大学学报（社会科学版），2001（2）：50。;其次，保障了所有维度得分区间的一致（均为[0，100%]），从而为后续通过权重实现不同维度得分的相加奠定了基础。

第一，流畅性维度的达成度d1，是指学生提出的有效数学问题的数量与测试题规定的满分时的数量之比。流畅性维度下，学生的得分S1为该题总分A乘流畅性维度的达成度d1，即S1=Ad1。

例1老师根据某一规则画出了图1所示的图形，请你根据所给的信息，从不同的角度提出6个数学问题。（12分）

……

对此，丙同学根据情境提出如下问题：（1）为什么要有黑点？（2）第3个图形的点数是多少？（3）第3个图形的比第2个图形多多少？（4）第5个到第10个图形一共有多少个黑点？（5）第11个图形的点数比第10个图形的点数多多少？（6）黑白点数之间的函数关系是什么？其中，问题（1）不属于数学问题，对本题而言是无效的;其他5个问题都是有效的。本题满分时要求提出6个有效问题，因此，该学生流畅性维度的达成度为56×100%=83.3%。本题满分为12分，则该学生流畅性维度的得分为10分。