丰富学习方式，内化数学素养

摘要：综合与实践活动是培养学生综合运用数学学科和跨学科的知识和方法解决实际问题能力的重要载体。在学生学完浙教版初中数学九年级下册第1章《解直角三角形》后，基于真实的生活情境，布置有一定挑战性的综合与实践活动任务“生活中物体的高度测量”，引导学生经历探索简易测量方法、了解现代测量工具、改进简易测量方法（工具）以及实地测量获得结果等过程，并对活动过程实施评价。这不仅提高了学生的综合运用能力和实践创新能力，而且丰富了学生的学习方式，内化了学生的数学素养。

关键词：初中数学；综合与实践；高度测量

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）依然将“综合与实践”作为与“数与代数”“图形与几何”“统计与概率”并列的课程内容的四个学习领域之一。新课标指出：“综合与实践以培养学生综合运用所学知识和方法解决实际问题的能力为目标，根据不同学段学生特点，以跨学科主题学习为主，适当采用主题式学习和项目式学习的方式，设计情境真实、较为复杂的问题，引导学生综合运用数学学科和跨学科的知识与方法解决问题。”②“进一步加强综合与实践”活动，“着力培养学生的应用意识、创新意识、实践能力、社会担当等品质”，教学时要“明确教学目标”，“设计教学活动”（包括活动任务的设计布置与完成引导等），“关注教学评价”②。

笔者在多年的日常教学中，积极践行综合与实践的课程理念。本文介绍一个活动案例：“生活中物体的高度测量”。

一、教学设计与实施

（一）明确教学目标

浙教版初中数学教材在九年级上册“4.5 相似三角形的性质及应用”的例6中给出了测量树高的两种方法，要求学生依据所给测量数据计算求解树高，并延伸提问：还有其他测量树高的方法吗？在九年级下册“1.3 解直角三角形”后的“设计题”中介绍了可用来测量观察目标时的仰角和俯角的测倾仪，要求学生说明测量原理并展开测量实践。

据此，我们在学生学完九年级下册第1章《解直角三角形》之后，尝试组织学生开展综合与实践活动“生活中物体的高度测量”，旨在让学生经历观察测量对象、探索测量方法、选择或制作测量工具、构建测量模型、拟定测量方案、实际测量以及完成测量报告、交流测量报告的过程。具体的教学目标如下：

1.了解物体高度测量的不同方法与原理，能利用相似三角形、解直角三角形等数学知识，选用不同的方法测量特定物体的高度，提高数学建模和数学抽象等核心素养，培养应用意识；

2.通过动手设计和制作测量工具，了解测量原理，并在使用中改进测量工具；学会实地测量，记录数据，撰写报告，评估结果，提升直观想象、逻辑推理、数学运算、数据分析等核心素养，增强实践能力，发展问题提出能力，促进反思性思维与批判性思维；

3.通过小组合作学习，将数学知识运用于真实问题的解决中，培养数学交流能力、手脑结合能力；了解古今中外高度测量的方法，渗透数学史，激发学习兴趣，提升数学情感。

（二）布置活动任务

我们设计并布置了如下活动任务：

同学们，秋天来了，校园的银杏叶开始凋落，你是否驻足思考过：这棵银杏树有多高？校园中和学校外还有哪些可望不可即的物体的高度？你能想办法测量它们吗？

请自行组合3—5位同学为一组，完成以下任务：

1.上网搜索测量物体高度的方法；（建议关注金字塔、树高等）

2.了解测量物体高度的相关工具；（建议了解测倾仪、测高器等）

3.确定待测物体，规划测量方法；（建议关注校园中的银杏树和旗杆、学校附近的住宅楼等，自制测量工具）

4.实地测量，记录数据并撰写报告；（建议多次测量并估算测量误差）

5.展示测量结果和分享体会。

（三）引导完成任务

1.探索简易测量方法

学生上网搜索历史上与生活中利用简易工具测量树高或楼高等的一些方法，教师引导学生理清背后的原理，然后基于相应的原理拓展得到更多的方法。

学生搜索得到的方法主要有：

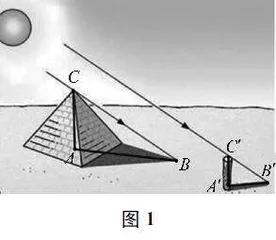
（1）影子法。古希腊数学家泰勒斯利用这一方法测金字塔的高度：如图1所示，因为斜射的太阳光是平行光，再利用竖直和水平的两组对应边，便可得到两个相似的三角形ABC和A′B′C′。其中，AC是金字塔的高度，AB是金字塔的影长加底面边长的一半，A′C′是标杆的高度，A′B′是标杆的影长。

根据相似三角形对应边成比例的性质，只要测得AB、A′C′、A′B′的长度，便可算出AC的长度。泰勒斯为了计算方便，特地以自己为标杆，并选择在自己的影长等于身高时测量金字塔的影长。

（2）标杆法。如图2所示，在地面上立一根标杆EF，沿着直线BF后退到点D，使眼睛C、标杆顶端E、物体顶部A在同一条直线上，量出人到标杆的水平距离CG和人到物体的水平距离CH，结合人的身高CD和标杆的高度EF，利用三角形CHA和CGE相似，就可以求出物体的高度AB。或者，如图3所示，用手举一根标杆EF，使之与地面垂直，并恰好挡住物体（即眼睛C、标杆顶端E、物体顶部A在同一条直线上，且眼睛C、标杆底端F、物体底部B也在同一条直线上），量出人到标杆的水平距离CG和人到物体的水平距离CH，结合标杆的高度EF，利用三角形CBA和CFE相似，也可以求出物体的高度AB。

（3）三角板法。如图4所示，手持含30°角的三角板，使得与30°角相邻的直角边保持水平；调整人的位置，使得眼睛从斜边恰好看到树顶；再量出人到树的水平距离AD，然后利用30°角（∠FAG，即∠CAD）的正切值，即可求得人眼以上的树高CD；加上眼高AB，即可得到树高CE。

教师引导学生理清方法1、方法2的原理：将要测物体的高度放在一个三角形（可以但不必是直角三角形）中，使得其中至少有一条线段可以量出，再寻找一个与之相似的三角形，使得其中与前一个三角形中需要求出和可以量出的两条线段对应的线段都可以量出，由此根据相似三角形对应线段成比例的性质，便可求出要测物体的高度。再理清方法3的原理：将要测物体的高度放在一个直角三角形中（通常作为一条直角边），使得其中有一个锐角和一条边（通常是另一条直角边）可以量出，由此利用相应的三角函数值，便可求出要测物体的高度。

由此，学生在充分认识了相似三角形模型和锐角三角函数模型的现实意义和相互关系的基础上发散思维，拓展得到更多的方法：

（4）镜子法。如图5所示，利用激光笔进行镜面反射，因为入射角等于反射角，得到分别以人高和树高为一条直角边长的两个相似的直角三角形……

（5）刻度尺法。如图6所示，用可以读出刻度量出不固定长度的直尺代替方法2中的标杆……

（6）量角器法。如图7所示，用可以读出刻度量出不固定角度的量角器代替方法3中含30°角的三角板……

在此基础上，教师引导学生从理论层面分析这些方法的优劣。学生普遍认为三角板法和量角器法比较简单。教师引导学生进一步认识到，相似三角形主要是基于角相等（形状相同）的定性的数学模型，而锐角三角函数则是基于角大小的定量的数学模型，同时前者是后者的基础，所以后者使用更方便。

2.了解现代测量工具

探索测量方法及其原理后，教师带领学生了解现代测量高度的工具，为学生进一步认识测量方法及其原理的应用提供支撑，并为自制测量工具（改进简易测量方法）提供借鉴。

首先是相对简单的测倾仪（如图8所示），可以用来测量观察目标的仰角和俯角。测量前，先将支杆插入地面，并使度盘直径PH处于水平位置，此时支杆的中心线、铅垂线和度盘的0刻度线重合。测量时，转动度盘，使度盘的直径PH对准测量目标顶端，这时铅垂线指向的刻度线即为仰角或俯角的度数。可见，这就是一个能更精准（更容易掌控水平和垂直）地测量仰角和俯角的量角器。

其次是更为复杂的测高器（如图9所示），可以直接测量观察目标的高度，使用起来比测倾仪方便。观测筒中的目测孔与准星构成了一条观测线；表盘上有六圈刻度，最里面一圈是仰角或俯角的度数，外面五圈分别是到测量目标的水平距离为8 m、15 m、20 m、30 m、40 m（五条“基线”）的情况下各仰角或俯角对应的测量高度。测量前，先用卷尺量取一条“基线”。测量时，让观测线对准测量目标顶端，这时不仅可以在表盘上读出仰角或俯角的度数，还可以由“基线”直接读出仰角或俯角对应的测量高度；加上测量者的眼高，即可得到物体高度。显然，这一仪器使用的测量方法就是上述量角器法，只不过设计者事先根据测量原理算出了不同水平距离下各个仰角或俯角对应的高度，将其标示在了表盘上。

最后是较为高级的激光（超声波）测高（测距）仪。它用激光（超声波）发送和接收信号测量长度和角度。设计者根据解直角三角形知识，将高度计算公式（算法）植入仪器中。使用时，只要分别瞄准测量目标的低点和高点，由内置算法的计算器自动计算，屏幕就能显示高度。

3.改进简易测量方法（工具）

在初步的测量尝试中，教师引导学生进一步从实践层面分析上述方法的优劣，发现每一种方法都有一些缺陷：影子法对天气要求较高；使用镜子法时，用激光笔定位的操作困难；使用标杆法、三角板法时，很难保证三点一线以及竖直或水平；使用刻度尺法、量角器法时，读取长度、角度的误差较大。

对此，教师引导学生尝试改进这些方法，并重点改进基于锐角三角函数知识的三角板法和量角器法。

首先，改进三角板法。为了保证三点一线，学生先想用激光笔，但发现在室外的远处确定光点比较困难。怎么办呢？学生联系测高器观测筒的构造，想到可以在三角板的斜边上制作两个准星。为了保证与30°角相邻的直角边水平，学生想到放置水平仪。由此，学生设计出改进的测量工具（如下页图10所示），并且在教师的帮助下，利用木条或金属线制作出这一工具。此外，受到测高器等工具能直接读出或快速显示高度的启发，学生进一步利用锐角三角函数知识，得到根据测量数据计算所求高度的公式H=h0l0l+h（其中，测量者的眼高h随时可以测得，改进工具的竖直高度h0和水平宽度l0在工具制作完成后即可测得，在实际测量中，只要测出测量者到待测物体的水平距离l，即可算出待测物体的高度H），并且画出测量操作示意图（如图11所示）。

其次，优化量角器法。为了减少读数误差，学生联系测倾仪的构造，想到利用大量角器（教师用的）和跳高支架制作改良版测量工具——测角仪。他们用一根铁钉穿过大量角器的圆心，并在铁钉上系一根细线，细线的另一端系一个小重物，然后把带有铁钉的大量角器固定在跳高支架上（如图12所示）。同样地，学生进一步利用锐角三角函数知识，得到根据测量数据计算所求高度的公式H=ltan（α-90°）+h（其中，测角仪的高度h在工具制作完成后即可测得，在实际测量中，只要测出测角仪到待测物体的水平距离l和大量角器零刻度线指向待测物体顶端时铅垂线指向的角度α，即可算出待测物体的高度H），并且画出测量操作示意图（如图13所示）。

4.获得实地测量结果

改进测量方法（工具）后，教师带领学生利用自制工具，实地测量校园中的银杏树和旗杆、学校附近的住宅楼的高度。通过多次测量取平均值，学生得到了测量结果，生成了数据报告。一组学生的测量结果与实际高度的误差如表1所示。

可见，自制测量工具不仅使用较为方便，而且误差较小。但随着物体高度的增加，误差也在增加。当然，这和物体顶端不明确有一定的关系。比如，旗杆的最高处是一个小球体，最高点较难确定；住宅楼的最上方也没有固定的瞄准点。

（四）实施教学评价

本次综合与实践活动的评价包括学生自评和教师评价两部分。

学生自评采取定量和定性相结合的评价方式，分细目进行。定量评价的内容如下页表2所示。

定性评价的内容如下：

1.你在项目活动中运用到哪些数学知识和能力？请详细列举。

2.请你用文字进一步描述在这项目活动过程中，你的收获：_____________________________；

你的困惑：_____________________________；