基于度量思想的整体性教学策略研究

［摘 要］通过聚焦某一单元的核心概念进行整体性教学，可以显著提升课堂效率。文章以度量思想为核心，探讨了“小方格度量策略”“分数单位度量策略”“小棒度量策略”的实践应用，结果显示师生负担得以显著减轻，学生的已有经验得到有效利用且思维能力得到了深层次的提升。

［关键词］整体性教学；核心概念；度量思想

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）23-0048-03

一、研究背景

当前，如何减轻学生的课业负担，实现减负不减质，是一个刻不容缓的课题。笔者经过近一年的课堂观察，发现直接影响课堂效率的主要原因有以下三个方面。

（一）课堂不分主次，眉毛胡子一把抓

在教学中，教师如果只根据教材设计教学内容，对学生的学情了解不够深入，就会导致课堂不分主次，眉毛胡子一把抓。课后发现学生基础不够扎实，转而又陷入“题海战术”的盲区，从而极大地增加学生的课业负担。郑毓信教授指出，我们应当跳出每一堂课的具体设计，从更大的范围进行思考，从而达到相关知识的深层次理解。因此，教师要区分清楚什么是主要内容和次要内容，并在教学中突出重点，由主要内容带动教学。

（二）教学就事论事，没有进行精准的提炼

在自主探究活动的反馈交流环节，课堂上师生一问一答，容易形成拉锯战，往往得不到预期的结论。造成这种现象的原因是教师不明确活动目标，对活动的认识只停留在完成任务，之后究竟要得到什么样的结论和提炼出何种思想方法，教师心里不清楚。

（三）知识点之间缺少沟通，学生自主迁移能力不足

数学知识点之间往往相互联系。课堂中，部分教师没有意识到知识点之间可以沟通和联系起来，只是零散地教授，导致学生只知其一不知其二，学习迁移能力薄弱。特级教师俞正强指出，要以发展代替重复。为此，教师应切实加强同类型课程之间的类比，厘清它们之间的异同。

二、整体性教学的理论分析与教材分析

（一）理论分析

整体性教学是一种以“核心概念”为统领的教学方式，它强调不同教学内容之间的关联性。在整体性教学中，教师需要跳出细节，从更广泛的角度去分析和思考问题，并抓住重点，通过核心概念来统领教学，从而揭示事物的本质规律。

结合教学实践进一步思考可知，如果能够找到某一单元或主题内容的核心概念，教师只需引导学生弄清这个核心概念的内涵，其余次要内容可以由学生自己去领悟、发展和延伸。这样，核心概念便起到了提纲挈领的作用。

（二）教材分析

以人教版教材为例，其中渗透了许多度量思想的内容。比如，在教学整数时，用个、十、百、千等计数单位去度量；在教学小数时，用0.1、0.01、0.001等计数单位去度量；在教学分数时，用分数单位去度量；在教学长度、面积、体积时，用单位长度、单位面积、单位体积去度量。可以说，教师若以度量的眼光去审视教材，就能发现其中处处蕴含着度量思想。

三、策略研究

结合以上分析，笔者在中高年段的教学中，尝试运用度量思想来开展实践教学。

（一）小方格度量策略

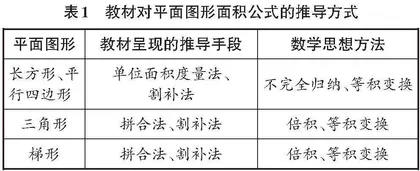
以五年级上册“多边形的面积”教学为例，教材对平面图形面积公式的推导方式见表1。

从以上分析可以看出，教材仅在教学平行四边形和长方形的面积时提及了单位面积度量法，但在教学三角形、梯形的面积时却没有提及。这就人为地割裂了学生的学习过程，导致知识点的断层。事实上，利用度量思想可以使学生自觉想到“转化”，从而沟通各知识间的联系。为此，笔者以“小方格度量的策略”开展了相关知识的实践研究。

1.平行四边形的面积

师（出示图1）：小正方形的边长是1 cm，先数一数图中平行四边形的面积，再验证。

生1（出示图2）：我是一格一格数，先数满格的，再数半格的，不满格都按半格计算，一共是21 cm²。

生2（出示图3）：我把左边的三角形移到右边，这样就拼成了一个长方形。数一数，刚好是21 cm²。

生3（出示图4）：我用了三种转化方法，也能得到平行四边形的面积是21 cm²。

师：为什么都用7×3=21（cm²）来计算平行四边形的面积？

生4：因为都是将平行四边形转化成了长方形，每行有7个小方格，一共有3行，所以都能用7×3=21（cm²）来计算。

【教学反思】推导平行四边形面积公式通常是脱离方格纸进行的，“数方格”的方法一直是次要内容，仅用于验证结果的正确性，这导致学生只能被动接受剪拼转化的方法。然而，将平行四边形放在方格纸上进行探究时，由于需要数方格，学生自然而然地会想到剪拼的方法，使转化变得自然且顺畅，这也为接下来学生学习三角形、梯形及组合图形的面积打下了良好的基础。

2.三角形的面积

师（出示图5）：小正方形的边长是1 cm，先数一数图中三角形的面积，再验证。

生1（出示图6-1）：我用的是复制粘贴法。

生2（出示图6-2）：我用的是割补法。

生3（出示图6-3）：我用的是复制粘贴割补法。

【教学反思】在用“数方格”来验证猜想的过程中，学生自然而然地联想到通过复制、粘贴、割补等方法将三角形转化为长方形或平行四边形，并且能够想出多元的转化方法。总之，有了度量思想这一核心概念之后，学生的自主学习便成为可能，思维也得到了发展，对问题的研究更加深入，学习的积极性也得到了很大的提高。

（二）分数单位度量策略

在教学五年级下册“分数的意义”时，采用分数单位来度量分数，学生能够从全新的视角来理解分数的意义。这种方法不仅帮助学生建立起分数与实际度量单位之间的联系，而且促进了他们对分数概念的深入理解和灵活运用。

生2：进率是4，满4进一。

师：只能数出4个分数吗？

师：如果一直数下去，能数出多少个分数呢？

生（齐）：无数个。

师：观察这些分数，为什么分母都是4？

生4：因为都是平均分成4份。

师：分子为什么不一样？

生6：因为计数单位的个数不一样。

【教学反思】让学生用分数单位数出不同的分数，实际上是用分数单位去度量不同的分数。在这个过程中，学生不仅明白了分数单位的含义，还学会了如何用分数单位去度量。这样，学生从全新的视角理解了分数的意义，同时也沟通了整数和分数的计数方式，即都是计数单位的不断累积。

（三）小棒度量策略

在教学五年级下册“2、3、5的倍数”时，笔者引导学生通过小棒进行度量，帮助他们理解各个计数单位的倍数特征。在掌握了2、3、5的倍数特征后，学生能够自主迁移，通过用小棒度量的方法发现4的倍数的规律和特征。

师：请用小棒分一分，探究为什么2、5的倍数只需看个位就能分辨出来。

生1：因为十位上的数，不管是2个2个地分，还是5个5个地分，都刚好分完，百位、千位亦是如此，所以只要看个位就能判断。

师：那么3、4的倍数的特征又是什么呢？

生2：用小棒3个3个地分，实际就是用3去度量，得出3的倍数的特征就是各位上的数字之和能被3整除。

生3：用小棒4个4个地分，发现百位及以上一定能4个4个刚好分完，所以只要看十位和个位。当十位上是0，2，4，6，8时，也刚好分完，这时只看个位就能判断；当十位上是1，3，5，7，9时，不能刚好分完，这时需要十位和个位一起来判断。

【教学反思】在研究倍数的特征时，由于2、5的倍数特征较为明显，教师通常不会采用分小棒的方式，这导致学生自主探索其他数倍数特征的能力较弱。通过始终使用小棒分一分的方法去度量需要判断的数，不仅能帮助学生学会知识，还能使他们学会自己研究倍数特征的方法。

四、策略反思

（一）整体性教学要提炼核心概念

以往的教学中，通常以转化思想为主导开展“多边形的面积”探究学习，而长方形、正方形的面积则以度量思想为统领。这种前后不一致，导致转化思想难以发挥应有的作用。结合学情和教材分析，笔者认为抓住度量思想就抓住了面积学习的本质，能够有效沟通长方形、正方形、三角形、梯形以及组合图形的面积。因此，应将度量思想提炼为核心概念，以统领整个单元的教学。

（二）核心概念的运用要一以贯之

教师要吃透教材，懂得做“减法”，明确哪些内容需要教，哪些不需要教，从而真正为自己的教学减负，也为学生的学习减负。如前所述，度量思想可以在很多领域中统领学生的学习。更重要的是，学生自己悟到的东西才是真正理解的，不容易忘记。关键是要一以贯之地运用核心概念进行教学，让学生能够自主迁移和发展。

（三）整体性教学让发展思维成为可能

在“多边形的面积”教学中，教师以度量思想为统领，使学生在格子图上自由发挥、深入思考，让其经历了“数格子”的过程和提出多种剪拼方法，激发了学生的思维，拓展了他们的眼界。在“三角形的面积”教学中，由于采用了“格子图”作为探究材料，学生不仅想到了“倍积法”，还想到了“割补法”，并能深入思考这两种方法的异同，从而真正理解了三角形的面积公式，记忆也更深刻。

综上所述，整体性教学是落实减负的一个很好的切入点，不仅能减轻教师的教学负担，还能增强学生的学习迁移能力，特别是帮助学生纠正“只见树木不见森林”的弊端。

［ 参 考 文 献 ］

[1] 郑毓信.数学深度教学的理论与实践[M].南京：江苏凤凰教育出版社，2020.

[2] 许卫兵.小学数学整体建构教学[M].上海：上海教育出版社，2021.

[3] 顾文.小学数学量感培养研究[J].小学数学教师，2023（3）：40-45.

[4] 李怀军.在度量教学中丰富学生的量感[J].小学教学（数学版），2021（5）：8-10.