情境感悟 意义建模

［摘 要］教师要挖掘知识的本质，抓住知识的内涵，探究现实情境蕴含的数学规律，引导学生经历“再发现”的过程，感悟数学思想，培养学生的模型意识，发展学生的高阶思维和核心素养。文章从引入情境、化繁为简、抽象概括、变式应用四个层次对“数学广角——植树问题”展开教学，并阐述如何培养学生的模型意识。

［关键词］植树问题；数学模型；情境

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）35-0057-04

数学模型将抽象的数学理论变成一种具体可感的图形。要培养学生的模型意识，就要在真实情境中发现和提出问题，探索运用基本的数量关系、几何直观、逻辑推理和其他学科的知识方法，综合分析与解决问题，增强应用和创新意识。

“数学广角”的“明线”涵盖了数学知识，“暗线”则将数学模型融入实际场景，涵盖了多种数学思想，如建模、数形结合等，旨在引导学生通过实践活动提高数学能力，让学生理解并运用知识。

一、引入情境

数学模型使数学知识回归真实情境，建构了数学与现实世界的联系。现在很多领域都会用到数学语言，除了数学符号，主要通过建立数学模型来刻画研究对象的性质、关系和规律。生活中有很多现象与“植树问题”类似，例如爬楼梯、锯木头、装路灯、摆花、挂灯笼等，这些现象都蕴含间隔数与物体数量之间的关系，理解“植树问题”的解决方法和策略，实现从“会解一道题”到“会解一类题”。

师（出示2个人夹球跑的图片，图略）：最近学校举行了运动会，大家最喜欢玩“夹球跑”的游戏。看这幅图，你能看到什么信息？

生1：有2个人，1个球。

师：如果3个人夹球跑，需要几个球？4个人夹球跑呢？5个人夹球跑呢？……

师：10个人夹球跑需要多少个球？

生2：9个球。

师：如果有15个球，那这一组一共有多少人？

生3：16人。

师：你发现了什么规律？

生4：1个球夹在2个人中间，球的数量比人数少1。

师：请用自己的话总结这个游戏的相同点。

生5：每两个人之间有一个空格，中间夹着一个球。

师：在数学中，这种空格叫作间隔，今天我们就学习与间隔相关的问题。

【设计意图】由学生最喜爱的游戏“夹球跑”导入，先观察2人夹球跑，得出只需要1个球的结论，再解决3人、4人、5人夹球跑的问题，接着提出“10个人夹球跑需要多少个球？”的问题。为了引出“间隔”的概念，教师没有直接给出解释，而是引导学生观察夹球跑的图片，让学生发现它们之间的共同点，从而引出“间隔”的含义。

二、化繁为简

《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）提出，学生要能在解决问题的过程中体会解决问题的道理，解释计算结果的实际意义，感悟数学与现实世界的关联，初步形成模型意识。在小学阶段，数量关系是学生形成模型意识的重要载体。寻找数量关系的过程中，我们需要引导学生运用化繁为简思想来探寻数量关系。

师：在100米长的小路一侧种树，每隔5米种1棵（两端都种），一共要种几棵树？

（分析题意，讨论间隔、间距、两端都种的含义）

生1：“每隔5米”是间距。

生2：每两棵树之间的空地是间隔。

生3：“两端都种”的意思是这条路的首尾都要种。

师：那么要种多少棵树？

生4：100÷5＝20（棵）。

生5：21棵。

师：请大家画一画，看看哪个答案是正确的。

生6：纸太小了，100米太长了，画不下。

生7：可以只画一小段。

师：把小路的长度改为20厘米，画一画，你有什么发现？

（学生画图后发现，每个间隔的长度是5厘米，20厘米中有4个这样的间隔，一共要种5棵树）

师：把比较大的数据改成比较小的数据来研究规律，这是数学中的化繁为简思想。

【设计意图】化繁为简思想对学生来说是一种新的解题方法，将题目中的大数据改小，容易推导出规律，并将其应用于实际的情况，从而高效求得结果，这是学生在解决问题时常用的方法，也是建模过程中常用的策略。

三、抽象概括

学生在数学思维方面需要经历从具体到抽象、从个别情况到普遍规律的发展过程。数学模型是对一类问题数量关系的抽象概括，掌握一个数学模型能解决一类问题。创设真实的问题情境，让学生尝试解决，呈现多样化的算法，在观察、对比、辨析中总结“植树问题”模型。

出示：学校思源楼旁有一条60米长的小路，为增添景观，学校计划在小路的一侧种树，并且要求两端都要种。请各小组设计一套植树方案，并填入表格。设计时应当考虑到株距、科学性和美观性，以确保植树方案的有效性和可持续性。

（小组合作，全班汇报交流）

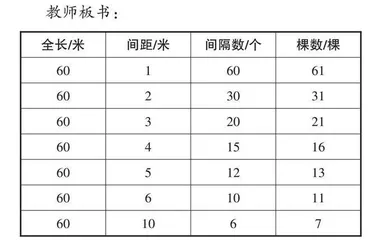
教师板书：

师：在一条直路上种树，两端都种，你发现了什么规律？

生1：路的长度除以间距等于间隔数。

生2：比较表格中间隔数和棵数这两列数据，我发现两端都种时，棵数比间隔数多1。

（教师总结并板书：间隔数=总长÷间距，棵数=间隔数+1）

师：这就是我们要学习的两端都种的植树问题。

师：以上哪个植树方案合适？说说你的理由。

生3：我认为间距3米的方案合适，间距刚好，绿化面积大。

生4：间距10米合适，这样有利于树木的生长。

……

师：根据绿化部门的要求，行道树的种植间距一般是6～8米，这样既有利于树木的生长，也能美化环境。

【设计意图】归纳法可以分为两种：完全归纳法，即仅仅从某个特定的数据开始，通过分析其内部的关系来推断其本质；不完全归纳法，需要从大范围探索内在规律，并从多个角度推断本质。这个环节运用不完全归纳法，通过表格的形式展示方法的多样化，进而发现规律，抽象出两端都种的“植树问题”模型，得出解决问题的策略。

四、变式应用

香港大学比格斯教授首创SOLO分类评价法，根据学生的回答能力、思路、一致性和相对收敛程度、整体结构的特征，把学习过程分成五个层次：前结构、单点结构、多点结构、关联结构、抽象拓展。不断构建真实的问题情境，让学生充分应用模型理解抽象结构，学生的思维水平将从第一层次逐步走向第四、第五层次，慢慢地从具体走向抽象，形成模型意识。

（一）解决同类问题

出示题1：金州路上有100个巨型中国结，每两个中国结之间挂1个灯笼，需要多少个灯笼？

生1：灯笼挂在每两个中国结之间，也就是挂在间隔处，100个中国结之间共有99个间隔，需要99个灯笼。

出示题2：广场上的大钟，几时整就敲几下，到6时整敲6下，每隔3秒敲一下，第一下和第六下之间间隔几秒？

师：我们模拟敲钟，咚……咚……咚……每隔3秒敲一下就是把敲击后的延长音看成间隔，敲到第六下就不用算其后面延长的声音，一共有5个间隔，“第一下和第六下之间间隔了几秒？”求的是5个间隔时间之和，因此一共间隔了3×5=15（秒）。

出示题3：王老师的家每两层楼之间有16级台阶。王老师一共走了64级台阶，王老师家在几楼？

生2（模拟走楼梯的过程，并结合“植树问题”模型）：16级台阶是1个间隔，64级台阶就是4个间隔，可以得出王老师家在5楼。

（二）提出同类问题

师：出一道与“植树问题”同类的题目，考一考你的同学。

生1：在一条长50米的跑道一侧，从头到尾每隔5米插1面彩旗，一共要插多少面彩旗？

生2：一辆公共汽车的行驶路线总长度为30千米，每两站之间的距离均为3千米，这条路线一共设置了多少个站点？

生3：把一根木头锯成8段，锯一次用2分钟，一共需要多少分钟？

师：大家学会了“植树问题”模型，要在各种不同的问题中去感悟、运用这个数学模型，加深理解。

【设计意图】《课程标准》指出，数学作为一门通用的学科，在许多学科中被广泛应用，运用学过的知识和方法解决简单的实际问题，养成理论联系实际的习惯，发展实践能力。教师根据长度、间隔数、棵数三个关键因素，创设了挂灯笼、敲钟、爬楼梯的生活情境，学生学会迁移类推、举一反三，利用“植树问题”模型提出其他问题，实现模型思想的萌发、成熟和发展，最终在比较、分析的过程中内化模型，发展核心素养。

五、教学总结

培养学生的模型意识，需要把握三个要点：一是注重在多样的情境中感知数学模型的抽象过程，从夹球跑、植树、爬楼梯、挂灯笼等问题中，强化学生对模型的感觉与体悟；二是注重在建模过程中丰富建构数学模型的具身过程，让学生经历将生活问题数学化的过程，解释生活中的问题，感悟模型的关联性、抽象性与丰富性；三是注重在实际运用中感受模型的基本式与变式之间的关系，积累应用模型的经验。

《课程标准》强调，数学是一种能够描述和解释现实世界的有效工具，它可以帮助人们建立一系列适用于日常生活和其他学科的模型，从而有效解决问题。本节课紧扣“植树问题”模型，从表象到本质，从特殊到一般，从生活经验到数学模型，层层递进，环环相扣，为发展学生的高阶思维，设计了引入情境、化繁为简、抽象概括、变式应用四个教学层次。

层次一：引入情境。引入“夹球跑”游戏情境，目的是使学生初步体验“植树问题”中的长度、间隔数、棵数等要素，学生体会到生活与数学的紧密联系。

层次二：化繁为简。目的是使学生在解决“植树问题”的过程中真实感受化繁为简思想，步步推理，经历解决问题的过程。

层次三：抽象概括。教学“植树问题”的目的不是简单地重复解题，而是让学生对模型深入感悟，归纳提炼出一般规律，形成对模型的普适性的深刻感悟。

层次四：变式应用。目的是让学生用“植树问题”模型解决生活问题，增强模型应用意识，为形成模型观念打下坚实的基础。

整节课创设多个真实的生活情境，注重识别情境中的信息，根据信息发现问题、提出问题，引导学生经历数学化的过程。学生运用操作、图形、符号等多种方式表征题意，分析数量关系，抽象出“植树问题”模型，用算式进行表达和解释，通过比较不同的情境，体会到“植树问题”模型的普遍性，提升模型意识。

［ 参 考 文 献 ］

［1］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022.

［2］ 刘琳娜，刘加霞.模型意识的内涵、评价维度及表现标准：以“有趣的搭配”单元为例［J］.小学教学（数学版），2024（3）：4-8.

［3］ 章勤琼，陈肖颖.小学数学模型意识的内涵、表现与教学：兼论核心素养的表现性目标［J］.课程·教材·教法，2024（1）：106-113.

［4］ 吴成业.“数学广角”中的数学思想方法挖掘：以《植树问题》教学为例［J］.教育研究与评论（小学教育教学），2017（9）：80-82.

［5］ 郑璘玲.从“个”到“类”    探寻模型建构之路：以《数学广角——植树问题》为例［J］.福建教育，2022（1）：55-56.

（责编    黄    露）