“三角形的内角和”教学中的“变教为学”

［摘 要］“变教为学”已成为新的教学潮流受到热捧，但是很多时候却被误读和曲解，教师只是从形式上削弱了教学行为，单纯增加操作活动量，却不放手让学生自主学习。真正的“变教为学”应该是教师科学设计操作活动，充分发挥学生的主观能动性，激发学生的好奇心和探究欲，引导学生自主发现、总结规律。

［关键词］三角形的内角和；变教为学；角度

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2023）02-0056-03

“三角形的内角和”这一知识点在小学教材和初中教材里均有编排。这一定理的完整表述应当是“平面上任意三角形的内角和都是180°”，“平面上”这个大前提非常必要，且凸显出数学的严谨性，一旦这个前提条件有变，那么结论将会不同，比如球面上的三角形的内角和大于180°。

一、追寻数学历史的脚印

科学史籍上最早关于“三角形的内角和”的记载出现在古希腊欧几里德著述的《原本》第三十二个命题中。这个命题主要包括两个结论，第一个结论是“任意三角形的一个外角等于与其不相邻的两个内角之和”，第二个结论是“三角形三个内角之和可以换算成两个直角”。原文之所以这样晦涩，是因为当时还没有“度”这个计量单位，数学界通行的办法是用直角和平角作为度量标准，来测量一切几何角度，角的两条边张开程度小于直角的角一律称为锐角，角的两条边张开程度大于直角的角一律称为钝角，比平角小的角一律称为劣角，比平角大的角一律称为优角。

17世纪法国数学家布莱兹·帕斯卡12岁时，在用小棒拼摆出各种几何图形的过程中，无意间证明了《原本》中的命题结论之一：三角形三个内角之和可以换算成两个直角。他的父亲知道后非常惊讶，于是将《原本》推荐给他阅读，帕斯卡很快就无师自通。

在我国小学数学教学中，有时会提到这个经典故事，目的就是为了体现数学的历史文化性。但是有些学生会误将帕斯卡当作“三角形的内角和是180°”这个结论的首创者。这一内容一般出现在四年级或五年级教材中，学生的年纪与当时证明出“三角形三个内角之和可以换算成两个直角”的帕斯卡相当，因此教师一般会顺水推舟，借此故事激励学生上进。其实，帕斯卡的过人之处不仅在于能证实这个结论，更在于他对数学的痴迷和热爱，他即使在摆弄小棒，也不忘思考问题，这样的精神值得学生学习。

“变教为学”的前提是要激发学生的兴趣。当学生对一件事漠不关心或者对某个知识态度冷淡时，是不可能“变教为学”的，教师一个劲地教，而学生则是勉勉强强地学。对于三角形内角和定理，通过设置悬念，是可以在一定程度上激起学生的学习兴趣的，但这个定理没什么趣味性，也很难据此设计出好玩的情境，因此，学生对此的态度还是不冷不热。而通过对三角形内角和定理历史故事的追溯，可以极大激发学生的兴趣，尤其是帕斯卡的故事，更是能激起学生的斗志，他们会按捺不住内心的敬佩和冲动，试图去看看这个定理到底有多简单，才能被一个12岁的孩子破解，说不定自己也能做到。再加上对历史进行考究，发现由于当时没有“度”这个单位，最早的三角形内角和定理与当今教材的表述不太一样，学生就会急于想知道那时的内角和定理的真面貌。

二、用任务驱动激发学生的主动性

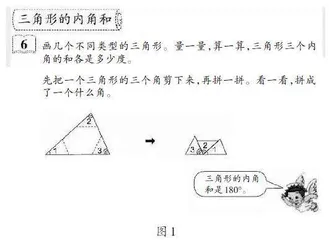
人教版教材中设计了两个学习任务（如图1）。

任务一：画出几个不同的三角形，算出各个三角形的内角和。

任务二：先将一个三角形的三个内角剪下来，再拼到一起，观察拼成了什么角。

这两个任务有一个共同点：直接告知操作流程和步骤。各环节都已经设计好了规定动作，这样牵着学生走，会使学生丧失创造力和独立思考精神。另外，这两个任务都是直接将探究目标和盘托出，结论“三角形的内角和是180°”会一直萦绕在学生脑海，学生不能在运动与变化中发现不变因素，“三角形的内角和是180°”这一结论的科学性和可靠性就会被淡化。实际上，“平面上任意三角形的内角和是180°”中的“任意”二字已经暗含了这一结论的客观性、科学性和普遍性。客观性指结论是真真切切存在的；科学性指结论是基于逻辑推理得出的，蕴含着某种事物的内部规律；普遍性指结论没有例外，强化了这一结论的本质属性。

这一结论从本质上应该一分为二。

结论一：平面上任意三角形的内角和为定值。这样的描述给三角形内角和定性，无论什么样的三角形，其内角和都是一个定量。然后，追问这个定量是多少就顺理成章了，可以顺水推舟得出定量描述。

结论二：这个定值是180°。这属于板上钉钉的定理，这是对客观规律的描述。

对于已经客观存在的规律，得出结论本质上是发现的过程，而不是发明。发现过程的关键思路是观察、对比、归纳。观察之前需要确定对象与动机，也就是思考“观察什么”和“为什么观察”等问题。根据观察到的现象初步得出的结论可以称为猜想，猜想往往是凭借直觉得出的，有时是错误的，后续要对猜想进行反复验证，直到得出科学合理而且经得起质疑和考验的结论，最后就是对结论的拓展与应用。

例如，在构建“对象与动机”一环中，教师设计了一个活动：随意画一个三角形，尽量放大其中一个内角，观察这个三角形的内角是怎么样的；再画一个三角形，尽量缩小其中两个内角，观察这个三角形的内角是怎么样的。

学生经过对比发现，如果三角形中的一个内角非常大，另外两个内角就非常小；一个内角再大也不会等于或大于180°。学生通过操作获得神奇有趣的发现，产生强烈的好奇心和探究欲，这种好奇心和探秘欲望会使学生一步步深入钻研知识。当学生感受到三个内角“此消彼长”的现象时，可能会将其迁移到加法运算中的和不变定律。与此同时，学生也可能猜到，三角形的内角和为定值，是固定不变的，这样就确立了下一步探究的目标。

“变教为学”主要强调学生的主动性，如果教师过多干涉，或者一开始就将结论和盘托出，学生再按照教师提供的操作步骤一步步求证结论，那么学生即使出错了，或者有了自己的想法，也不敢吱声，因为他们不敢反驳教师，这就谈不上“变教为学”了。要想做到“变教为学”，教师就要最大限度地放权，所有的提示和指导都要极尽模糊抽象，比如让学生比较多个三角形内角和的大小，但学生发现比不出大小，因为所有三角形的内角和都一样，既然一样，必为定值，接着就要确定这个定值是多少。这样一步步下来，三角形内角和定理就是学生自己发现的，而不是教师传授的。

三、验证方法多样化

规律性知识的特点是结论是唯一确定的，但是探究的方法和途径却是多种多样的。对三角形内角和定理的验证，在小学阶段，通常采用测算、剪接、拼贴的方法。这些方法直观形象，易操作，适合形象思维较强的小学生。到了初中一般采用两种方法证明。第一种类似《原本》中的方法，即应用同位角相等和内错角相等的结论，将三角形的三个内角转移到一块，组成一个平角（如图2）。

第二种是利用“任意多边形的外角和是360°”的定律来推导。三角形三个外角之和是360°，而每个内角与相应外角组成平角180°，可推算三角形的内角和为180°×3-360°=180°。

2011年4月，一本名为《Math Horizons》的杂志发表了一篇文章，其中给出了“三角形的内角和是180°”的操作性解释。

如图3所示，在一个三角形的左下顶点处放置一根与底边重合的火柴，然后不断旋转、平移这根火柴。

第一次：将火柴沿着内角顶点旋转，与另一边重合。

第二次：将火柴沿着重合的边平移至另一个顶点。

第三次：将火柴沿着顶点旋转至第三条边。

第四次：将火柴沿着这一边平移至第三个顶点处。

第五次：将火柴沿着顶点旋转至底部的边。

第六次：将火柴沿着底部的边平移至出发点。

此时，火柴回到原点。火柴的整个运动过程一共包含三次旋转和三次平移，旋转和平移交替进行。平移时火柴保持方向不变，引起火柴转向的主要是旋转，三次旋转的角度之和恰好就是三角形三个内角的和，最后火柴水平调头转向说明它整体旋转的角度是180°，这也就证明三角形的内角和是180°。

这一方法的优势在于运用动态变化证明了静态的几何规律。同时，用“角”这一概念来度量方向的变化，将平移与旋转的差别揭示出来，即平移运动是位置改变，方向不变，旋转运动则是位置和方向改变。

验证方法虽多样，但不是所有方法都适合小学生使用，比如利用内错角来证明对小学生来说是超纲的，利用外角和来证明也不合时宜，利用直观的裁剪拼凑法来证明也无法令人信服，因为直观操作的例子毕竟是有限的，属于不完全归纳，学生目前的联想能力和推理能力还不足以理解这种证明方法，也无法脑补出三角形三个内角凑到一起形成平角的景象。而利用火柴的旋转和平移来证明，则能轻松理解，因为平移和旋转是小学阶段必备的基本几何技能，学生通过平移和旋转的特性来理解火柴在三个内角处旋转三次，每次旋转的角度恰好就是所跨越的内角度数，一共旋转了三个内角度数之和，火柴最后回到初始位置，但是两端调头，说明三个内角和为180°。

“变教为学”倡导将教师的教学活动转化为学生的主动探究活动，师生的主体地位发生扭转。这种转变要想获得成功，必须有科学的学习任务和学习活动做支撑。“变教为学”中的操作活动，其实就是训练学生综合技能的机会。学习动机和学习方法是学习者保持学习热情的原动力。因此，教师在设计学习任务时，要设身处地为学生着想，让学生自觉学习，而不是被迫执行教师的指令，同时，在验证环节，要为学生创造自主探究的机会，让学生学会自主学习，牢牢掌握学习的主动权。

［ 参 考 文 献 ］

[1] 王亚.开展数学实验，提高教学的适切性：以苏教版小学数学四年级《多边形的内角和》一课教学为例[J].小学教学参考，2021（21）：10-11.

[2] 刘驰.利用教学资源   构建生命课堂：《多边形的内角和》教学设计[J].小学教学设计，2021（17）：51-53.

[3] 吴青.深刻理解内角概念   完善三角形内角和教学[J].课程教材教学研究（小教研究），2021（Z3）：42-46.

（责编 黄 露）