项目式学习：让学生在主动参与中达成概念性理解

［摘 要］项目式学习是以“儿童的”学习动机激发学生主动参与学习活动，以“全面的”投入学习促使学生深度理解，以“深入的”探讨交流直击知识内核，引领学生经历从“遇到问题”到“解决问题”的学习方式。文章以“长方形的面积”教学为例，通过项目式学习让学生悟出长方形面积公式的“度量”本质，使学生的思维经历从一维空间到二维空间的跨越，形成空间观念。

［关键词］项目式学习；长方形的面积；概念性理解

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2023）02-0063-03

【问题凝视】

学生在三年级学习了长方形的面积之后，往往就会混淆周长和面积。例如，要画一个面积为12平方厘米的长方形，总有学生画成周长是12厘米的长方形。又如，学生会把一个长方形的面积写成12厘米。

【成因分析】

1.学生空间观念发展不足，没有实现从一维空间到二维空间的跨越

学生很难精准表达线与面的联系和区别，如受长度测量的影响，在比较长方形面积的大小时，学生第一时间会去测量其长和宽，而对于不规则的图形，学生就无从下手。可见，学生对“面”的认知还停留在一维空间的层面，在他们的认知中，“长×宽”和“长+宽”意思差不多，所以即使他们做再多的练习，也还是把面积算成周长。从一维空间到二维空间的跨越是学生空间观念一次重要的飞跃，如果不能让学生从二维的角度来辨析面积的本质，那么后续的学习也就成为空中楼阁。

2.面积公式理解不足，仅局限于记忆

面积公式的本质是度量，即用数和单位刻画图形面积的大小。而对于问题“为什么会混淆长方形的面积和周长”，学生的回答是“因为它们都用长和宽来计算”。从学生的回答来看，学生对面积公式仅限于生硬记忆。若学生没有真正理解，又何谈掌握？

3.概念性理解不足，没有建立基础量感

对于问题“为什么把长方形的面积写成12厘米”，学生的回答是“‘平方厘米’中都有‘厘米’，两者差不多”。从学生的回答中可以看出，他们没有真正理解面积的本质，因而不清楚面积单位所表示的实际意义，更别说建立平方厘米、平方分米、平方米的量感了。学生对面积的概念的理解深度和广度不够，原因有两点，一是缺少辨析的过程，因此没有理解面积的本质；二是学生对面积单位缺少丰富的体验感知，获得的直接经验较少，因而无法建立清晰而精准的面积单位量感。

可见，学生只有高质量地主动参与数学活动，调动身体各部分充分感知“面积”，通过观察、操作储备清晰的表象，才能形成几何直观。

【探寻出路】

史宁中教授指出，学生空间观念的形成和发展，本质上是学生自己“悟”出来的，即通过独立思考以及和他人的讨论与反思，逐渐养成的一种思维习惯。要想“悟”得深刻，就得“感”得充分，而充分的“感”有赖于学生高质量地主动参与数学活动。

项目式学习以“项目活动”为载体，以“问题串”为引领。项目式学习的学习动机、学习过程、学习评价和探讨交流都旨在学生主动参与，引导学生在项目中发展能力、提升核心素养。

1.“儿童的”学习动机驱动主动参与

乔纳森在《学习环境的理论基础》中明确指出“学和做是不可分的，它们都是由意图启动的”。没有意图的学习，就没有主动意向，那学习就只能是一种抽象化的学习，并非真实的学习。要让学生积极主动参与，学习动机一定是属于“儿童的”。因为学生在真实的活动中有感而发、深有体悟的问题，所以可以激活他们的探究欲望，进而驱动他们积极主动参与学习。如在学生学习长方形的面积后，可以安排一个小项目：班级需要一个课外活动场地，请用12米长的绳子去围一个长方形或者正方形的班级活动场地，场地面积要尽可能大。了解了项目要求后，有的学生拿着绳子的一头跑得很远，以至于绳子不够，最终没有围成长方形或是正方形；有的学生总怕绳子不够，围得很小心，结果绳子剩了一段；有的学生很聪明，先用绳子围成一个圈，然后再将其拉成长方形。这样的一番操作下来，学生产生了疑惑：“到底哪个才是面积最大的呢？”。参与活动后产生的疑惑成为学生真正的学习动机，成功唤起他们的探究欲望，学生进而主动把现实问题抽象成数学问题——周长和面积的关系，最终调动已有的知识经验进行探究，主动参与学习。

2.“全面的”投入学习促使深度理解

蒙台梭利认为：身体是学习过程的重要组成部分，我们的动作能辅助我们思考。当身体、大脑和思维都参与到探究过程中，学生才能进行深层次的思考。在项目活动中，学生对“哪组围成的场地面积最大？”有着急切的探究欲望，这就是情感的投入。如学生在学习“认识面积”后，获得用数方格来比较面积大小的经验及面积单位的知识，在教师的引导下就能想到先将每组围成的图形按比例画在方格纸上，再数一数方格数量，最终比出围成场地面积最大的小组。在优化数方格方法的过程中，学生明白长方形面积其实是“长方形一行的小方格个数×行数”，即“长×宽”。又或者再通过画一画、数一数、算一算，明白原来围成的场地面积是可以用边长为1米的方块来度量的，“长×宽”算出来的是方块的个数，从而理解面积与周长是不一样的。学生在多次“全面的”投入学习中明白了长和宽在面积公式中的实际意义，在沉浸式的学习中深度理解了面积公式的内涵。

3.“深入的”探讨交流直击知识内核

“深入的”探讨交流强调探讨要有深度，这意味着学生的思考、交流不能浅尝辄止。学生在探讨交流中慢慢理解知识背后所蕴含的原理和思想方法后，将原有的知识经验与新知建立联系，可将知识技能转化为能力素养。对“能否用简单的方法来测量长方形的面积”这一问题的探讨，学生的思考有：用什么来测量面积的大小呢？能用长度单位吗？为什么测量长和宽就能求出长方形的面积？学生经历了辨析长度单位和面积单位的不同过程，使面积单位的概念再次强化。学生的探讨不局限于单个问题的深入，而是一个接着一个问题的层层深入，直击面积公式内核：长方形周长公式的长、宽与面积公式中的长、宽代表的意义是一样的吗？学生在辨析中理解长方形周长公式中的长、宽是长度，而面积公式中的长、宽表示的是小方块一行的个数与行数，它们代表的意义不同。这样，在探究、比较、讨论中，学生逐步建立起稳定、清晰的认知，从本质上区分了面积与周长的不同，一维空间与二维空间的差别。在真实而又富有挑战性的问题中，学生不断深入探讨交流，逐步积累并形成经验。

项目虽小但能激发学生主动参与，精准的核心问题能引领学生沉浸式地思考、探讨，使其经历从“怎么围”“哪个面积最大”，到“数方格”，再到“公式计算”，最后到“与周长对比辨析”的过程。这样的教学将数学核心素养的培养落到了实处。

【教学重构片段】

1.实践探究，找寻测量面积的方法

师：大家在操场上用12米长的绳子围了各种不同的长方形和正方形。哪组围的面积最大？

组1：我们可以用数方格的方法比较面积的大小。

师：把每一块场地分割成一个个1平方厘米的小方块吗？

组1：围成的场地很大，用1平方厘米的小方块显然太小了，用手掌大的1平方分米的小方块似乎也太小。应该用1平方米的小方块。

师：还有别的想法吗？

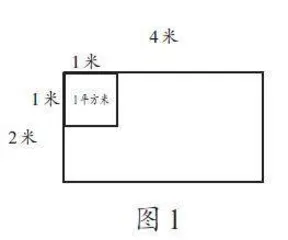
组2：我们组围的长方形长4米、宽2米，都是以米为单位，角上摆出的第一个方块的面积是1平方米。（如图1）

师：可以用1米长的绳子代替1平方米的方块来测量面积吗？为什么？

组3：1米长的绳子只能量出长度是几米，1平方米的方块可以量出几平方米，不能代替。（如图2）

（学生小组合作，划分场地后数方格）

2.探讨想象，提升测量面积的方法

师：数方格的时候，要一个一个数出来吗？

组1：我们组围成的图形长4米、宽2米。我们先数一行的方块数，有4个，再看有2行，一共8个方块，所以是8平方米。（如图3）

师（出示图4）：能知道这个长方形的面积吗？

组2：长4米就表示一行有4个1米，宽2米就是有2行，还是可以算出长方形的面积的。

师：你们的意思是用“每行的个数×行数”就可以知道长方形里面有几个方块，也就是用“长×宽”就可以知道长方形的面积。

3.沟通比较，理解面积公式

师（出示图5）：通过数这几个图形的面积的过程，你发现它们有什么相同之处和不同之处吗？

组1：都是一行有4个方块，有2行，面积都是8平方米。

组2：它们的不同之处是，有的是一个一个数，有的是只数了一行，有的不需要数。

组3：最后一个图形是看着数字想象方块数，就是将4米想象成一行有4个方块，将2米想象成2行。

组4：长是4米，一行就有4个方块，宽是2米，即2行，然后将长和宽相乘就能求出一共有几个方块。最后一个图形的面积是算出来的，不是数出来的。

师：“4×2”也就是“长×宽”，表示的是方块的个数，也就是这个长方形的面积。

师：如果一个长方形长10米、宽6米，能算出它的面积吗？

生1：10×6=60（平方米）。

师：请总结出求长方形面积的公式。

生2：长方形的面积=长×宽。

师：长方形的周长公式为“长方形的周长=（长+宽）×2”，长方形的周长公式和面积公式中的长、宽代表的意思是一样的吗？

组5：长方形周长中的长、宽表示的是长度，长4米表示有4个1米，宽2米表示有2个1米，“长+宽”一共有6个1米，周长就是12个1米。长方形面积中的长表示一行有几个方格，宽表示有几行，“长×宽”表示的是一共有多少个面积为1平方米的方格。

师：看来大家已经领悟面积公式的本质，并且能清楚地区分长方形面积与周长的不同了。

4.应用实践，巩固面积公式

师：我们再看看操场上围出的不同的长方形，现在要知道哪组围的面积最大，只要算出每组围成的图形面积就可以。能算吗？

生1：能。只要测量出每个长方形的长和宽，然后计算它们的乘积就可以了。

师：在围成的图形中，正方形的面积最大，它的面积是怎么求的？

生2：其实也是用一行的个数乘行数，只不过两个数是一样的。

师：我们的操场那么大，它的面积到底有多大呢？能测量吗？

生（齐）：能！

综上所述，项目式学习能激发学生主动参与学习活动，促使学生深度理解，引领学生经历从“遇到问题”到“解决问题”的过程，让数学核心素养的培养真正落地。

［ 参 考 文 献 ］

[1] 史宁中.数学基本思想与教学[M].北京：商务印书馆，2018.

[2] 马丁.教与学的新方法·数学[M].王嵘，译.北京：北京师范大学出版社，2004.

[3] 乔纳森.学习环境的理论基础.[M].郑太年，等，译.上海：华东师范大学出版社，2004：98.

[4] 余文森.核心素养导向的课堂教学[M].上海：上海教育出版社，2017.

【本文系江苏省教育科学“十三五”规划2020年度课题“基于儿童权利的小学生主动学习活动设计研究”阶段性成果。】

（责编 金 铃）