审辩式学习：在深度探究中思乐共生

［摘 要］在“三角形内角和”教学中，以“五学”课堂为学习路径，利用猜想、验证、转化等思想方法，鼓励学生积极、自信、理性地运用解释、分析、推理、评价等认知技能来解决数学问题，着眼于推进审辩式学习，对创新数学教学方法、培养学生审辩式思维具有一定的指导意义。

［关键词］三角形内角和；审辩式学习；“五学”课堂；审辩式思维

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2023）20-0004-05

【教学内容】北师大版教材四年级下册“三角形内角和”

【教学目标】

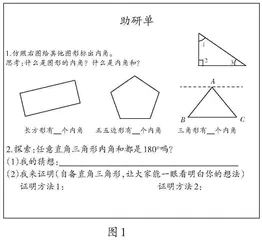
1.通过推算、测算、折拼、撕拼等操作活动，发现三角形内角和等于180°；

2.通过比较不同方法和对多边形内角和的探索，感受“转化”的数学思想，发展动手操作、推理分析能力；

3.在亲历探索发现的过程中，体验数学思考与探究的快乐，形成应用意识、创新意识和审辩式思维。

【教学重点】

1.在操作活动中发现“三角形内角和等于180°”的性质，体会“转化”数学思想的应用；

2.能根据操作活动清晰表达探索与发现的过程，发展推理分析能力和形成审辩式思维。

【学习准备】助研单、课件、三角形纸片（学生自备1套，教师自备2套）

【课前预学】

内角和的概念是本课的学习起点，教师可秉持“少教之教”的教学理念，对学生通过观察即可感悟的知识，只引导其辨析和加强认识。个体只有经历了体验，认识和思考才会深刻，也才能在小组交流或集中讨论时产生思维的碰撞。审辩式学习关注学生的独立思考，但课堂40分钟的时间往往不够进行充分的探索和体验，预学作业则能弥补这一缺失。

【课中共学】

一、创设情境，以问启学

1.感受推理

师（出示长方形）：这是一个长方形。它的角有什么特点？

生1：长方形的4个角都是直角。

师：长方形内角和是多少？

生（齐）：360°。

师：你们是怎么想的？

生2：因为每个角都是直角90°，4个直角就是4个90°，所以长方形内角和就是360°。

师：生2利用“4个角都是直角”这个已知信息，经过思考、计算，得出一个新的结论——长方形内角和是360°。我们把这个过程叫作推算。他在表达中用到“因为……所以……”这样的表达句式，使这个推算过程有理有据，令人信服。

2.引发思考

师：沿着这个长方形的对角线先折一次再剪开，得到2个大小相等的直角三角形。每个直角三角形内角和是多少？为什么？

生3：每个直角三角形的内角和都是180°，因为360°被平均分成了2份，每份就是180°。

师：非常棒！从已知信息出发，通过分析和计算，得出一个新的结论，这个方法就是推算。

师（出示大小、形状不一的直角三角形）：直角三角形有大有小，是不是所有直角三角形内角和都是180°呢？

《义务教育数学课程标准（2022年版）》在核心素养部分指出：通过经历独立的数学思维过程，学生能够合乎逻辑地解释或论证数学的基本方法与结论，分析、解决简单的数学问题和实际问题。在本环节中，学生先后经历两次推理过程，在教师的积极评价中感悟论证方法，体会有理有据及逻辑表达的重要性，并对直角三角形内角和展开从特殊到一般的思考。

二、猜想验证，以探入学

探索1：所有直角三角形内角和都是180°吗？

师：课前大家已经利用自己制作的直角三角形进行了验证，请汇报你的想法。

生1：我用的是推算的方法。（出示直角三角形）这是我的一个直角三角形，如果在它上面还有一个和它一样大小的直角三角形，就组成了一个长方形。长方形内角和是360°，那么它的一半，也就是这个直角三角形的内角和是180°。

师：大家听清楚了吗？有没有问题？

生2：这里只有一个直角三角形，它是怎么变成一个长方形的？

生1：你可以想象把这个直角三角形“翻过去”，就能得到一个长方形了。

师：生1让我们从一个直角三角形中看出长方形，这是培养我们的想象能力呢！除了推算的方法，还有别的方法吗？

生2：我用量角器先量出三角形每个角的度数，然后相加，算式是“90°+28°+50°=168°”。

生3：我是量直角三角板每个角的度数。“90°+30°+60°=180°”，还有“90°+45°+45°=180°”。

师：他们的结果不一样。大家怎么看呢？

生4：如果测量不准确就很容易出现误差。

师：生2，你可以向大家展示一下测量过程吗？

生2：我发现我测量的直角三角形有一条边没有画直。

师：没关系，你得出的不一样的结果，让大家知道探究的每个环节都不能马虎，正所谓“大胆猜想，小心求证”。还有其他的方法吗？

生5：我测量的2个角的度数分别是35°和55°，它们合起来是90°，加上第三个角——直角90°，就得到180°。

师：先测后算也是一种探究方法，关键是要小心测量，避免误差。

生6：我用的是折拼的办法。把这个直角三角形的2个锐角往直角所在的方向折，拼了拼后发现它们与三角形的直角重合，三角形的3个角就变成了2个直角。这样，这个直角三角形的内角和就是“90°×2=180°”。

师：生6先折再拼，把其中2个角合在一起后发现它们与已知的直角重合。这个把未知变成已知的过程就是转化思想的运用。还有别的想法吗？

生7：我用的也是折拼的方法。把这个直角三角形的3个角折起来可以拼成一个平角。平角是180°，所以这3个角的和，即这个直角三角形内角和也是180°。

生8：我也折过，发现拼的时候很容易有空隙，这样就不能确定是不是拼成了平角。

生9：我也觉得会有误差，所以我用了撕的方法，把3个角撕下来，然后拼在一起，就拼成了一个平角。

师：这几位同学的想法有什么共同的地方？

生10：他们都用到了“转化”，把3个角转化成一个平角。

师：是啊，不管是“折”还是“撕”，他们都运用了“转化”，活学活用，值得表扬！同时，有同学关注到“误差”“空隙”会导致“不能确定”，这种严谨的探究精神非常值得我们学习！

师（动画展示）：把直角三角形的3个角撕下来后可以拼成一个平角，我们就说直角三角形内角和是多少？

生（齐）：180°。

本环节中，在课前独立探究的基础上，学生经历了“猜想—验证”的过程，通过交流的方式畅谈探究方法和结果。在交流时，学生都能从现象出发，质疑问难、实事求是。

探索2：所有三角形内角和都是180°吗？

师：通过探索，我们知道了直角三角形内角和是180°。可是，三角形是会变化的。（课件展示将直角三角形直角顶点向上提）直角三角形现在变成了——

生（齐）：锐角三角形。

师：它还可能变成——

生（齐）：钝角三角形。

师：直角三角形、钝角三角形、锐角三角形，哪种的内角和最大，哪种的内角和最小？

生1：直角三角形内角和最大，锐角三角形内角和最小。

生2：我觉得钝角三角形内角和最大，锐角三角形内角和最小。

生3：我觉得三种三角形的内角和一样大。

师：能想办法验证自己的观点吗？请拿出钝角三角形和锐角三角形，用你喜欢的方法进行验证。

生4：我采用的是“撕拼”的方法。无论是钝角三角形，还是锐角三角形，“撕拼”后都能拼成平角，所以它们的内角和都是180°。也就是三种三角形的内角和一样大，都是180°。

师：生4既汇报了验证过程和结果，又汇报了自己的结论，有理有据。

生5：我用的是推算的方法。先把2个同样大小的锐角三角形拼在一起，发现拼成一个平行四边形，而不是长方形；再把这个平行四边形的一个角剪下来移到另一边，这样就变成了一个长方形；最后发现锐角三角形的3个角拼成了一个平角。也就是说，锐角三角形内角和是180°。

师：延续生5的方法，把2个同样大小的钝角三角形拼在一起，也能得到一个平行四边形。把平行四边形变成长方形后，观察角的位置，有什么发现？

生6：和锐角三角形一样，拼成了一个平角，推算出钝角三角形内角和是180°。

师：有没有用其他方法或得到其他结果的？之前大家给出了4种方法，为什么这里只用到撕拼和推算呢？

生7：我觉得这样比较准确，另外两种方法都容易产生误差。

师：大家得到的结论是什么？

生（齐）：任意三角形内角和一样大。

师：有同学一开始猜想的不对，但通过验证找到了正确结论，这就是“失败乃成功之母”。只要大胆猜想、小心求证，就会有成长、有进步，直至获得成功。

在“避免或减少误差”的要求下，学生自主选择验证方法，体现了优化思想。在“将平行四边形转化成长方形”的表达中，因为时间关系，学生只推算了锐角三角形的情况，教师不动声色地引导学生完成钝角三角形的推算，让验证过程不遗漏，交流过程更完善，产生的结论更有说服力。在这个过程中，积极中肯的评价让每个学生都能找到自己的亮点和成长点。

三、对话反思，以辩立学

师：学习到这里，你有什么收获？

生1：我知道“不管是哪种形状的三角形，内角和都是180°”。

生2：钝角三角形、锐角三角形、直角三角形的内角和一样大，都是180°。

师：谁能表述得更简洁一些？

生3：三角形内角和是180°。

生4：三角形内角和等于180°。

师：在“猜想—验证”的探索过程中，你有什么学习感受或心得？

生5：我觉得要尽量减少误差，不然就得不到正确的结论。

生6：我觉得“转化”很重要，任何平行四边形都可以转化成长方形。

师：看来大家虽然有共同的结论，但是对结论的获得有着各自的体会和思考。只要是科学的、带着我们走向正确结论的方法，我们都予以支持。

通过反思，学生能够及时梳理新知，学会用确的语言描述三角形内角和的性质，加深对验证方法的思考，对不同方法能够包容和理解。

四、拓展探究，以用成学

师：沿一块三角形纸板上任意直线剪一刀，剩下纸板的内角和是多少度？先猜想，然后动手操作验证。小组之间可以互相交流，看看你们的想法是不是一样。

生1（出示图2）：我是这样剪的。剪后剩下的纸板是一个三角形，它的内角和是180°。

生2（出示图3）：我剪掉了一个角，剩下的纸板是一个四边形，它的内角和是360°。

师：你是怎么知道的呢？

生2：我把这个四边形折了一下，得到2个三角形。一个三角形内角和是180°，2个三角形的内角和就是360°。

师：活学活用，能利用“转化”把四边形转化成三角形再推算。

师（出示五边形和六边形）：它们的内角和分别是多少？独立思考后再小组交流。

生3（出示图4-1、4-2）：五边形可以转化成3个三角形，内角和是180°×3=540°；六边形可以转化成4个三角形，内角和是180°×4=720°。 

师（出示图5）：从这些内容中你有什么发现？

生4：它们的内角和依次增加180°。