“用错”三部曲

【摘要】数学学习中，必然会有学生出错的情况。对于学生出错，要喜用错因、善用错因、用足错因。对于学生的错，不必急于否定，要用足错误的机遇，等来绽放的花开。本文实录课堂教学中几个片段，展示教师指导学生自主思考、实现思维进阶的过程，化错误为机遇，变“事故”为“故事”。

【关键词】用错  三部曲  画垂线

【中图分类号】G623.5   【文献标识码】A 【文章编号】2095-3089（2024）11-0148-03

数学学习中，学生出错是必然的，没有出错的学习过程不是真实的学习过程，也是不必要的学习活动。那么，学生出错了，教师应该有怎样的反应？安徽特级教师朱森明指出，学生出错“错皆有因”，教师要“闻错则喜”，要“喜用错因、善用错因、用足错因”。对此，笔者在教学“画垂线”一课的片段中，获得了深切感受。

一、喜用错因

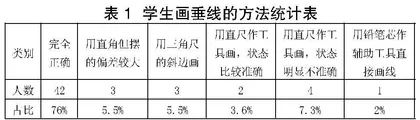
片段一：教学苏教版四年级上册“认识垂线”一课，让学生过直线外一点画已知直线的垂线。巡视中发现，有学生画得不太符合要求。安排这个学生把画的过程重复一遍，该生拿着三角尺，用尺的斜边竖对着已知直线，就画出了垂线，画的过程没有用到三角尺的直角。基于这种情况，再安排全班学生都把三角尺摆好，我逐个检查，发现了更多问题，全班55名学生情况如表1所示。

出错的13名学生中，用标准工具的6人，7人没用标准工具。就第三类用三角尺斜边作图的3名学生，我请学生说说原因，有1人是不知道方法，另外2个学生说这样画方便一些。

思考：针对两个学生说“方便一些”，我深入思考，在以前教学中也有类似例子。例如，学生不愿意验算、假验算；简单的列方程解应用题，学生不愿意用方程法，选择算术法。他们觉得方便快捷最重要，以前老师们都说这是不良习惯，要求学生必须改正，按标准要求去做。这样处置，是不是最好的方式呢？如果学生提出，为什么必须按要求去做呢？

商务心理学中有个概念是“求便心理”，指产品设计要充分考虑顾客“追求方便”的心理需求，设计产品必须让顾客方便使用。生活中，追求方便可以说是人的天性，只要有不同方案可选，一定自动选择最省事的。不能简单地认为这是坏事，事实上自然界多数事物都自动符合求便规则，简洁化也能让世界发展的进程加快。就数学学习来说，学生学习简便运算、活用转化策略等，正是“求便心理”的合理应用，数学总是把常用法则总结为公式和定理，也是基于这个需要。新课标对此指出，要指导学生选择合理简洁的运算策略解决问题，欣赏数学语言的简洁与优美。

既然不能简单否定学生图省事的心理，那么教师就不能简单斥责学生。本着呵护这一最原始的“健康心理”和“优质动机”，教师应该如大禹治水，疏导而不硬堵。再者，反思教师自己，我在第一轮巡视时，也是凭着自己的估测经验估的，在课堂巡视中，估测更加符合课堂需要，我不可能用三角尺一个个去测量的。在批改作业时，老师们也总是这样，只有觉得可能存在问题时，才偶尔用三角尺去测量，对认为比较准确的，或者明显误差很大时，总是凭经验直接评对错。

片段二：看谁画得又快又准。先安排学生赛一赛，直线外一点作已知直线的垂线，看谁更快；再相互评价作得准不准，如果觉得不准，要用道理说服对方；最后议一议，你有什么体会？

思考：这里让学生拥有自主纠偏的权利，为了说服对方，几乎所有学生都意识到，只有用三角尺的直角去验证，才能让对方信服。因此，学生也自省明白：随意画只能是“大概”而并非“一定准确”。有了学生的自我反省，教师可以提示，数学是严谨的，在没有让我们估测时，要准确就必须借助科学的工具。

商务运营学指出，“求便心理”会让人有意选择最快的流程，直达结果，但流程简化，意味着系统简化，那么系统操作的稳定性就会下降，难达到最优化的结果，所以“便捷性”与“稳定性”要综合考虑。本课中这个“要综合考虑”的道理，正是在学生赛一赛之后，自我认识到的。

喜用错因，教师要有充分的耐心，给予学生自我悟错的时间，提供学生自我识错的突破口，不应包办代替，而是静等花开。

二、善用错因

片段三：如果没有三角尺，怎么办？

师：刚才同学们都明白了，准确作图必须借助工具，如三角尺等。那么，如果不使用三角形尺，能不能尽量准确地作出垂线呢？（学生合作探究，教师巡视）

生1：我用量角器，让90°的刻度线经过点，就可以画出来了。

生2：我用书本的直角靠着画的。

生3：我用直尺画，不过我把直尺竖着经过上面的点，再观察相交处连着的两个角，慢慢调整，觉得这两个角一样大了，就应该是互相垂直了，因为这时候这两个角都是直角（如图1）。

生4：我和他（生3）同桌，所以方法一样，不过我是用细的笔芯摆的，看两个角相等了，然后画线的。

生5：我用折的办法，经过上面的点，把纸竖着左右对折，让直线的两边重合，这时候，顺着折痕画就行（如图2）。

生6：我也是用直尺，我是直尺的边压着那个点，让直尺绕着点旋转，观察这点到线上交点的长度，什么时候长度最短了，就应该是垂线了。

师：其实生1也是工具，量角器与三角尺同样是科学的工具，是精确作图，不过三角尺更方便一些；生2是类似书法上的“临摹”，是摹出来的，也比较准确，只要书的直角准，画出来就比较准；生3、生4用了中学几何学的一些道理，方法是完全对的，当然只用眼睛看，不一定能完全准确；生5的折纸法很神奇，这个方法与生3有相似处，不过用折纸代替了直尺、笔芯，本质上还是使相邻的两个角都是直角；生6用了一个重要的数学道理，即过直线外一点，和直线上的点所连线段中，垂直的线段最短。需要说明的是，表面上看，后面几位同学没有用工具，其实是“工具在脑中”，“脑中工具”也很重要。

思考：在前面学生有了一定自我反省的基础上，没有止步，还向着学生喜欢的方向——“估测画”拓展，让前面“问题点”蝶变成新知的“生长点”，让实物“有形尺”变成脑中“无形尺”，新经验由学生自己悟得，抽象能力得以提升。新课标指出，要勇于探索一些开放性的、非常规的实际问题与数学问题，培养创新意识，创新意识有助于形成独立思考、敢于质疑的科学态度与理性精神。

三、用足错因

如果仅仅止步于此，就未能用足错因，于是，课程继续向深度和广度进行拓展。

片段4：上面不同的方法，其合理性是什么？

生1：用量角器画，用书的角来画，我觉得与用三角尺画差不多，它们都是上面有一个直角。

生2：在用直尺旋转，或者用笔芯、折纸，当两个相邻角相等时，每个角都是平角的一半，就是直角。

《义务教育数学课程标准（2022年版）》指出，数学学习要让学生经历数学“再发现”的过程 ，发展质疑问难的批判性思维，形成实事求是的科学态度，初步养成讲道理、有条理的思维品质，逐步形成理性精神。

师：第6个同学说的“长度最短”是符合要求的，课本上对此有说明。想一想，为什么长度最短时，就是已知直线的垂线？请同学们也用直尺旋转摆一摆，看看有什么发现？

生：当连线最短时，相邻的两个角就相等，都是直角。

师：为什么不是最短时，相邻的两个角就不能都是直角？请用小棒、笔芯摆一摆，或者画一画，看看有什么发现？（学生活动）

生：我反过来想的，我摆出来这个图，左侧的甲牙签都已经摆歪了，如果此时还能和横线垂直的话，那么对称地看，在右侧应该就有一个乙牙签，也一定能和横线垂直。不过这时两个牙签和横线组出来一个三角形区域。我们知道直角是90°，那三角形中就出现了两个90°，但这是不可能的。（如图3）。

师：从三角形状态来分析，可以得出道理，当然，三角形中是能有直角的，三角尺是个三角形，其中就有一个直角，不过，不能有两个直角。这个知识以后的课程中能够研究到。既然不能有两个直角，就不可能过直线外一点，画出这条直线的两条不同垂线，就是这个同学说的，摆歪了，就不可能是垂线。可是为什么摆正了，就一定是垂线呢？老师这里有个作图工具——圆规，在五年级学习中会用到，今天提前借用这个工具，请同学上来试试，能不能用圆规作图来发现更多的道理。（选不同学生反复演示）

生：画出不同的圆形，当圆和直线刚刚碰上时，就是摆正了的情况，这时候，碰上的那个点就是垂足。如果画小了碰不上不行，如果画大了，就有两个位置，就是前面两个摆歪了的位置，画出来的都不是垂线。（如图4）

师：这是一个中学知识，称为直线和圆相切状态。有兴趣的同学，可以课外网上搜索看一看。

对于直线外一点和直线上的点所连线段中，垂直的线段最短，书上有说明，限于小学生的知识和经验，不能解释。但通过摆一摆、画一画，学生能得到类似的感悟。新课标指出，要引导学生初步感受认识直尺和圆规在作图中的简单应用。小学的简单的尺规作图应用，正是第四学段中深入学习尺规作图的基础。曹培英就图形与几何教学指出，让学生经历操作感悟画法，再理解几何关系。由小棒摆，到用圆规画，最后感悟出相切状态时符合要求（隐含的知识）。

片段5：目测比赛

用两根磁棒摆放在黑板上，红色棒横着，让学生竖着摆绿色棒，然后其余学生估测准不准，说出估测方法，提出调整方案，全部认可后，选学生用三角尺验证。

再将这个活动，复制成生生互动的同桌赛。

师：同学们已经有了很强的目测能力，不过，如果要追求精准，就必须借助科学的工具。

思考：顺着学生的“错”，曲线解决问题，顺势发展了学生的估测能力，又回指了要点“严谨的作图必须是借助工具”，估测与精准互补，依据情况而定。有趣的是，到课程结束时，反而学生都自觉用三角尺去验证。

对于学生的错，不必急于否定，要用足错误的机遇，等来绽放的花开。