读思达：小学生数学语言表达能力提升三步骤

【摘要】小学生数学语言表达能力的培养是一个程序化、序列化的系统过程。本文以小学数学问题解决的教学为例，遵循“读→思→达”路径探寻小学生数学语言表达能力提升的基本步骤，一方面帮助学生形成问题解决的意识、掌握解决问题的策略，另一方面促进小学生“三会”核心素养的落地。

【关键词】读思达  数学语言表达能力

【基金项目】本文系福建省教育科学“十四五”规划 2021年度课题《核心素养背景下提升小学生数学语言表达能力实践研究》研究成果，课题编号：FJJKZX21-648。

【中图分类号】G623.5   【文献标识码】A 【文章编号】2095-3089（2023）08-0067-03

“读思达”教学法是余文森于2021年提出的，这一教学法的理论依据来自认知加工理论。余文森指出学习本质上就是一种认知的过程，完整的认知过程包括认知输入、认知加工、认知输出三个环节。与此相对应，完整的学习过程也包括阅读、思考、表达三个环节[1]。2022年义务教育数学课程标准把“三会”作为学生核心素养的构成要素，具体为会用数学的眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界[2]。从教学的角度看，“三会”与认知加工理论中的三个环节不谋而合：在观察中读，为信息输入铺路；在思维中思，为信息加工导航；在语言中达，为信息输出赋能。基于这些认识和理解，笔者以小学数学问题解决为例，探寻小学生数学语言表达能力提升的基本步骤。

一、读：厘清脉络，为信息输入铺路

从学生认知的角度来说，读是基础和前提，是学生与文本的对话[1]。数学问题的呈现形式是多种多样的，因此教师可以通过读文、读图、读表等方式来读懂题目中的相关信息，在头脑中重建题干文本，从而发现问题并提出问题。

1.全面感知数学信息

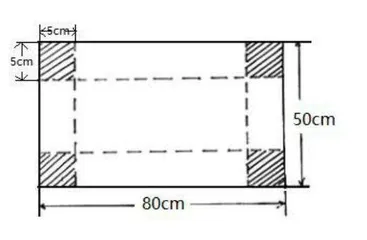
首先，引导学生通过粗读，了解题干中的文字信息、图片信息、表格信息等。读的时候可以默读也可以读出声，但不可以漏读，要把题干的信息读完整读明白；其次，要引导学生通过细读，在题干中找出重点词或重点句，可以采用边读边标记的方式增强对题干信息的理解[3]。请看这道题：从一块长方形铁板上剪去四个边长为5cm的正方形，用剩余部分焊接成一个铁盒。粗读中，学生会发现“这个长方形的长是80cm、宽是50cm，从长方形的四个角上分别剪去一个边长为5cm的正方形”。学生在描述这些数学信息的时候要引导其注意信息的先后顺序，这样便于学生更好地理解题干信息。细读中，学生又会发现“用剩余的部分焊接成一个铁盒”这个重要的数学信息。有了粗读和细读做铺垫，学生的脑海里迸发了“焊接成的这个铁盒是什么形状？它的长是多少？宽是多少？高是多少？它的体积是多少？它的表面积是多少？……”一系列数学问题。

2.细致梳理关键信息

当学生遇到一道题干信息冗长的数学问题时，内心可能是不安的也可能是崩溃的。此时，应引导学生利用画线段图、矩形图、表格图等方式细致梳理关键信息，让数学信息可视化、清晰化。如：厦门地铁收费标准：起步价为2元4公里（含4公里）。超过4公里后，4～12公里（含12公里）：按4公里加收1元计费（不足4公里按4公里计费）；12～18公里（含18公里）：按6公里加收1元计费（不足6公里按6公里计费）；18～28公里（含28公里）：按10公里加收1元计费（不足10公里按10公里计费）；28～43公里（含43公里）：按15公里加收1元计费（不足15公里按15公里计费）；43公里以上：按每20公里加收1元计费（不足20公里按20公里计费）。镇海路站到厦门北站大约29.02公里，需要花费多少钱？这是一道典型的分段计费问题。借助线段图，学生可以清楚地看到厦门地铁收费的具体分段情况，而镇海路站到厦门北站的总公里数29.02公里处于28公里到43公里之间，根据“不足15公里按15公里计费”这一信息把29.02公里看成43公里。这样一来，需要花费的总价格包括了图上的五个阶段，只要先分别算出每个阶段的收费总价，再把它们加起来就完成了。

3.深入挖掘潜藏信息

数学信息的呈现有一些是浮在表面的，也有一些数学信息是潜藏在题干下方的，需要学生通过对比观察、深入分析才能挖掘出来。教师可以这样来引导学生：你知道了什么？你还能想到什么？如：小明用一张梯形纸做折纸游戏，先上下对折使两底重合，可得图1。此时，测出未重叠部分的两个三角形面积和是20cm2。然后再将图1中两个空白小三角形部分向内翻折，得到图2。经测算，图2的面积相当于图1的。那么，这张梯形纸的面积是多少cm2？读题中，学生不难发现图1中左下角和右下角两个三角形的面积和是20cm2，但对于“图2的面积相当于图1的”这个数学信息始终把握不了。此时，教师应该引导学生对比图1和图2，找到两图相差的1份在图2左下角和右下角两个空白三角形的面积和，即20÷2=10（cm2）。当这一潜藏的数学信息被挖掘出来的时候，本道题的解题思路就浮出水面了。

二、思：抓住关键，为信息加工导航

从学生认知的角度来说，思是关键和核心，是学生与自我的对话[1]。当学生读完题，厘清了题目中的所有信息脉络后，信息输入已顺利完成。此时，教师应该引导学生不断与自我对话，借助图形、示意图、线段图、表格等工具探索解决问题的思路，为分析问题提供脚手架。

1.借助表格描述问题

实践表明，虽然有些数学问题信息描述得十分浅显，可学生在实际答题的过程中仍然困难重重。此时，教师可以引导学生借助表格，分别从横向和纵向两个角度切入进行思考，打开思维之窗。如：文体店中，两个毽子卖7元，五根跳绳卖32元。为了奖励在数学小达人活动中表现进步的同学，钟老师准备买10个毽子和20根跳绳，一共要花多少钱？横向观察中，学生本想借助“总价÷数量=单价”这一数量关系先得出毽子和跳绳的单价，但由于学生还没有小数除法的认知基础故无法解决这个问题，于是采用纵向观察，学生的思路一下子明朗了起来。由于10个毽子是2个毽子的5倍，所以10个毽子的总价就是2个毽子总价的5倍，采用10÷2×7就可以得出10个毽子的总价。跳绳总价的解决思路同理可得。当学生分别算出10个毽子和20根跳绳的总价再相加，本题就不攻自破了。

2.借助图形凸显卡点

数学问题的情境是抽象的，学生分析问题时存在一定的困难。因此，教师要引导学生养成画图的习惯，借助图形去分析问题，凸显问题解决的卡点。如：小明测量了一个平行四边形的底、邻边和高的长度，可是他只记得三个数据6cm、5cm和4cm，但忘记了这三个数据分别对应的是哪条边？你能根据这些数学信息算出这个平行四边形的面积有多大吗？读题中，学生不难知道解决这个问题的关键是找出这个平行四边形的底和高分别是多少厘米，但如何才能又快又准地找出这个平行四边形的底和高呢？通过画图把这三个数据进行排列组合，不重复也不遗漏得到六种答案，结合“直角三角形的斜边大于直角边”这一原理推理得出图2、图4、图6才是符合条件的。因此，原来这个平行四边形的面积可能是6×4=24（cm2）或者5×4=20（cm2）。

3.借助线段图分析数量关系

分析数量关系是小学阶段解决问题的关键，线段图能将题中抽象的数量关系以形象、直观的方式表达出来，学生依据线段图分析数量关系能又快又好地帮助学生解决问题。如：一辆轿车和一辆货车同时从甲、乙两城出发，相向而行，两车在距中点15km处相遇。轿车每小时行60km，货车每小时行52km。甲、乙两城相距多少km？通过画线段图，学生很容易发现：轿车比货车多行驶的路程为15+15=30（km），用30km除以两车的速度差就能求出相遇时间，再用速度和乘相遇时间就能求出两城之间的距离。即：（15+15）÷（60-52）=3.75（小时）、（60+52）×3.75=420（km）

三、达：对话交流，为信息输出赋能

从学生认知的角度来说，达是归宿和提升，是学生与他人对话[1]。在表达和倾听的过程中，同伴们分享彼此的认识、经验和见解，更正、补充、丰富彼此的看法。当学生在与文本、与自我进行深入对话，厘清题目中的所有信息脉络以及抓住解题关键后，信息输入和信息加工才算顺利完成。此时，教师应引导学生采用语言、文字、图形等多种表征方式，为信息的输出赋能，让问题的解决过程简洁清晰地呈现在同伴或教师面前，主要有以下两种方式：

1.口头表达，让信息输出立体化

数学语言是数学知识的载体，又是数学思维的工具，当学生能够准确地将自己的思维过程或思维结果用数学语言通过口头表达出来时，头脑里处于混沌状态的思维活动才能逐渐被清晰起来。因此，教师首先要善于把握学生的心理，创设宽容和谐的氛围，激发学生用数学语言表达的欲望[4]。如：提供对话平台，让学生以四人小组为单位上台展示。一人主讲，一人板书，其他两人补充，班级其他同学当听众，倾听之后提出自己不一样的看法。又如：鼓励开展亲子说理互动，让说数学变得和做数学一样有趣有味。再如：依托公众号平台，鼓励学生录制说理视频并发表。其次，学生在进行口头语言表达时要遵循一定的表达技巧：一用支架性语言让学生言之有物[5]，如：（  ）的排列规律是以（  ）为一组依次重复出现，学生循着这个框架就可以清晰流畅准确地表达他所看到的规律。二用关键性语言让学生言之有序，如：“我先由……想到……，列式是……”这样的语言。三用推理性语言让学生言之有据，如：先通过剪、移、拼把平行四边形转化为长方形，通过观察发现平行四边形的底等于长方形的底、平行四边形的高等于长方形的宽，因为长方形的面积=长×宽，所以平行四边形的面积=底×高。

2.书面表达，让信息输出结构化

数学问题解决的思维过程和思维结果除了可以用口头语言表达，还可以用书面语言来表达。学生通过思考，在相应的答题处将自己的所思所想记录到纸面上，同伴或教师通过阅读纸面上呈现出来的答题过程了解该学生的答题思路。实践中，教师常常会发现有些学生由于缺乏规范，常常出现过程不清、表达不力这两种现象。因此，教师应引导学生采用三段论的方式进行表达，让书面表达呈现结构化。如：1米的和7米的一样长吗？说说你的理由。这是一道说理题，学生从分数的意义出发，可以借助文字或借助算式进行描述。首先阐述过程，其次说明理由，最后呈现结论，让内在思维过程跃然纸上。学生的书面表达需要经过系统训练，因此教师要有意识地引领：可以从日常的板书示范、标答示范、要求规范等方面入手；也可以让学生先在脑海中将思路过一遍，然后再用纸笔记录下来；最后还要回顾反思整个过程。

总之，经过两年的实践和摸索，笔者认为遵循“在读中抽象，厘清脉络为信息输入铺路；在思中推理，抓住关键为信息加工导航；在达中建模，对话交流为信息输出赋能。”这样三个步骤，小学生数学语言表达能力得到了显著的提升。

参考文献：

[1]余文森.论“读思达”教学法[J].课程·教材·教法，2021，41（4）：50-57.

[2]教育部.义务教育数学课程标准（2022年版）[S].北京师范大学出版社，2022.

[3]金永梅.小学数学解决问题策略的生成路径[J].教学与管理，2020（29）：52-54.

[4]庄敏.小学生数学语言表达能力的培养[J].数理化解题研究，2020（8）：50-51

[5]李帮魁.小学生数学语言表达的类型及培养[J].教学与管理，2020（14）：54-55