大数据专业“概率论与数理统计”课程的实验教学案例研究

【摘    要】数据科学与大数据技术专业主要学习的用于数学计算和数据分析的软件有R语言、Python、MATLAB、SPSS等。“概率论与数理统计”是一门基础数学课程，理论性较强，相对枯燥，利用Python和MATLAB软件对概率计算、仿真、数值模拟方面的实验案例进行探究，可以帮助学生更好地理解和掌握概率论与数理统计的知识和方法，提高学习兴趣和学习效果，同时，可将理论知识转化为实际应用，增强学生的实践操作能力。学生掌握大数据软件的使用和概率论与数理统计的知识，可以使其快速适应未来职业发展的需求，为未来的工作做好准备。

【关键词】“概率论与数理统计”课程；实验教学；Python；数值模拟

【引用格式】王永娟，姚艳，范英兵.大数据专业“概率论与数理统计”课程的实验教学案例研究[J].黑龙江教育（理论与实践），2025，79（3）：76-78.

【中图分类号】G640；TP391.6             【文献标识码】A             【文章编号】1002-4107（2025）03-0076-03

一、引言

随着科学技术的发展和社会现代化的推进，社会对大数据科学的研究与应用型人才的需求与日俱增。数据科学与大数据技术专业是近年来国家针对“大数据”时代背景新增的专业[1]。概率论与数理统计是统计学和数据挖掘的理论基础，在大数据相关专业中尤为重要。大数据的价值体现在其蕴含的规律上，而对数据进行处理、分析离不开统计学和数据挖掘。利用概率论与数理统计的原理对数据中各个属性进行统计、分析，找出数据蕴含的规律，让其创造价值，是大数据专业学生必须掌握的基本理论知识，更是大部分学生未来工作和生活的必备技能。

在概率论与数理统计实验中，经常需要处理大量的数据以验证或探索统计规律。大数据软件能够处理和分析大规模、复杂的数据集，极大地提高数据处理的效率和准确性，使实验结果更加可靠和精确[2]。同时，大数据专业软件具有丰富的数据可视化功能，能够将数据以图表、图像等形式展示出来，通过可视化，学生和教师可以更直观地理解数据的分布、趋势和关系，从而更深入地掌握相关概念和方法。大数据专业软件还通常包含强大的数据挖掘和机器学习功能，可以帮助学生发现数据中的隐藏模式和关联，探索新的统计规律和知识。而这对于培养学生的创新思维和实践能力具有重要作用，有助于学生在未来的科研和工作中更好地应用概率论与数理统计知识。

数据科学与大数据技术专业主要学习的用于数学计算和数据分析的软件有R语言、Python、MATLAB、SPSS等，而“概率论与数理统计”课程可以应用的软件主要有Python、MATLAB和R语言，应用在概率及随机变量数字特征计算、绘制与验证分布函数及密度函数图像、数值模拟、参数估计、假设检验等内容[3]。文章对相关软件在概率计算、验证分布函数、数值模拟等方面的案例进行探究，帮助学生快速计算的同时，增加动手实践的机会，更好地理解理论内容。

二、Python软件在概率计算中的实验案例

Python软件在概率计算中的应用广泛且灵活。在实验中，可以使用NumPy库来生成随机变量样本，并计算其概率分布。例如，通过NumPy库的random模块，可以模拟抛硬币的过程，计算正面和反面出现的概率。同时，

SciPy库也提供了丰富的统计函数，可用于计算各种概率分布的参数、概率密度函数值及累积分布函数值等。这些功能使得Python成为概率计算的有力工具[4]。三门问题是概率论中的经典问题，以贝叶斯公式求解三门问题为例，介绍笔算和软件算法，让学生体会换门与不换门概率变化的过程，同时，启发学生对程序进行修改，实现此问题的多种算法表达。

【三门问题】假设你参加一个游戏，要求在三扇门中选择一扇：一扇门后是汽车，另两扇门后是山羊。当你选择了一扇门但未开启前，知道门后秘密的主持人开启了剩下两扇门中的一扇，露出山羊，这时你会改变原来的选择吗？

问题分析：假设参赛者一开始选择了门A，那么汽车在A后面的概率是1/3，也就是说中奖的概率是1/3，未中奖的概率是2/3。假设此时主持人打开了有山羊的B门后，排除了一个没有中奖的情况，利用贝叶斯公式可以算得，此时参赛者选择换门中奖的概率即为2/3。在利用贝叶斯公式进行实际笔算过程中，将问题拆解成在A、B、C任一门后有汽车的情况下B门被打开的概率，此时学生不容易理解，这时可以用Python软件将换门后中奖的所有情况罗列出来，通过古典概型进行计算，使学生更容易理解。

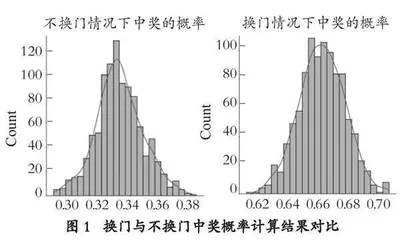
通过Python中的random.choice函数实现随机放奖品与随机选门，通过def自定义函数对换门与不换门进行模拟，最终计算结果如图1所示。利用软件能帮助学生理解换门与不换门的思维过程，图像展示结果，验证了三门问题的数学结论，即换门是一个更好的策略。该实践加深了学生对概率论中条件概率和独立事件的理解，提供了一种直观的方式来解释和解决看似复杂的概率问题。

三、Python软件在仿真中的实验案例

在“概率论与数理统计”课程中，使用Python软件进行仿真是一种非常有效的教学方法，可以帮助学生直观地理解抽象的概念和原理。如模拟投掷硬币的过程并计算正面出现的概率；模拟利用蒙特卡洛法估计圆周率π；模拟二项分布，当试验次数很大且成功概率适中时，二项分布近似于正态分布。使用Python软件进行仿真时，常用的库包括用于离散事件仿真的SimPy库、数据处理与分析的Pandas库、数值计算的NumPy库和数据可视化的Matplotlib等[5]。以下利用Python软件模拟高尔顿钉板实验，模拟小球下落过程，绘制小球下落位置图像，使学生深入理解概率论与数理统计的概念和原理。

【高尔顿钉板】高尔顿钉板（图2），常常在赌博游戏中见到，即庄家通常在两边放置值钱的东西来吸引顾客。现在可用中心极限定理来揭穿这一赌博中的奥秘[6]。

问题分析：假设有n排钉子，记随机变量Xi表示第i次碰钉后小球从左边或右边落下，左边落下记作1，右边落下记作-1，Xi服从两点分布，n次碰钉后小球的位置服从正态分布，所以，落在中间的概率远远大于落在两边的概率。通过Python软件可以对小球下落过程进行模拟，并绘制出多个小球下落后的概率分布图像。

利用Matplotlib库中函数实现可视化，主程序中主要使用for循环、if语句实现多个小球下落后的频率分布曲线。

进行3组实验，小球落下位置的概率结果如图3所示。通过动态展示小球下落过程，可以观察到正态分布的形成过程，让学生体会看似无序但实则有规律的运动。同时，启发学生思考随机性、确定性和无序性之间的关系，从而拓展思维视野。

四、MATLAB软件在数值模拟中的实验案例

通过MATLAB软件展示“概率论与数理统计”课程中的一些基本概念和定理，如模拟泊松分布并绘制其概率分布函数图像；模拟数据进行线性回归分析，生成正态分布的随机样本并绘制直方图等。通过数值模拟，学生可以更直观地理解这些概念和定理，并学会使用MATLAB软件进行相关的数值计算和可视化。MATLAB软件用于数值模拟的函数丰富多样，包括用于曲线拟合的polyfit（）函数、进行参数估计的最大似然法和矩法函数、实现插值运算的一维插值和样条插值函数，以及用于微分方程求

解的ode45函数等。以下为利用MATLAB软件模拟中心极限定理，演示原分布为不同分布时，极限分布为正态分布的案例。

【中心极限定理】设随机变量X1，X2，…Xn，…相互独立，服从同一分布，且 这个定理表明，当n充分大时，n个具有期望和方差的独立同分布的随机变之和近似服从正态分布。虽然在一般情况下，很难求出X1+X2+…+Xn+…的分布的确切形式，但当n很大时，可以求其近似的分布[7]。单看定理内容比较难理解，此时可利用MATLAB软件在X1，X2，…Xn，…服从二项分布、泊松分布、指数分布和伽马分布4种情况下，模拟其和的概率分布函数[8]，如图4所示。

以单变量服从二项分布为例，首先，利用res定义单变量表达式、构造和函数表达式，利用Gamma函数生成变量随机数，histogram函数绘制单变量直方图；其次，计算出均值和标准差后，用normpdf函数计算正态分布的概率密度函数[9]；最后，用plot（）函数画出伯努利试验总次数分别为10、20、200、600，概率均为0.5的情况的直方图与概率密度图像。通过图像对比，学生体会随着试验次数的增加，二项分布和的分布趋近于正态分布的效果。图4a为实验总次数为200、概率为0.5时的拟合效果图。

是离散型还是连续型，随着试验次数的增多，其和都近似服从正态分布。通过图形对比，增强了中心极限定理的可信度，同时，使枯燥的定理学习变得更加生动有趣，提高了学生学习兴趣和学习效果[10]。

五、结束语

“概率论与数理统计”课程为数据科学与大数据技术专业提供了方法支持，在大数据处理和分析中，需要运用概率论与数理统计的原理和方法对数据进行描述、推断和预测。利用大数据软件解决“概率论与数理统计”课程                中心极限定理为统计推断提供了理论基础，在实际

应用中，经常需要根据样本数据推断总体的特征，而中心极限定理可以建立置信区间和假设检验等统计推断的方法，是非常重要的定理。通过对比图4可知，无论单变量

中的问题，可以提高学生的实践能力和动手能力。学生运用所学的理论知识，结合软件工具，对数据进行处理、分析和建模。这种实践过程可以帮助学生将理论知识转化为实际应用，增强学生的实践操作能力。引入大数据专业软件，可以促进“概率论与数理统计”课程与现代信息技术的融合，推动课程教学的改革和创新。这种融合不仅能够提高学生的学习兴趣和积极性，还可以培养学生的数据素养和数据处理能力，为未来的职业发展打下坚实基础。

【参   考   文   献】

[1]  谢桃枫，曹莉.概率论与数理统计的教学研究：基于数据科学与大数据技术专业[J].教育教学论坛，2020（45）：299-300.

[2]  胡嘉卉.实验辅助概率论与数理统计教学的应用实践[J].数学学习与研究，2021（32）：2-4.

[3]  王永娟，姜喜春，谢兵兵.Python在概率论与数理统计教学中的应用案例研究[J].黑河学院学报，2022，13（9）：104-105.

[4]  邹丽珊.基于Python的“概率论与数理统计”课程实验可视化研究[J].安徽电子信息职业技术学院学报，2024，23（1）：49-54.

[5]  肖进胜，杨力衡，丁玲，等.现代数理统计中假设检验的教学探讨[J].高教学刊，2024，10（8）：117-120.

[6]  吴赣昌.概率论与数理统计[M].北京：中国人民大学出版社，2022：102-105.

[7]  王伟珠.论中心极限定理及应用[J].赤峰学院学报（自然科学版），2013，29（19）：1-2.

[8]  章美月.基于Mathematica的《概率论与数理统计》课程教学改革探索与实践[J].大学数学，2020，36（5）：49-56.

[9]  李守彩，崔建新，候军丽.基于BOPPPS模式的“中级财务会计”课程探究式课堂教学改革研究与实践[J].黑龙江教育（理论与实践），2024，78（10）：71-74.

[10]  韩凌波，李晓玉，石丽梅.面向新工科的“MATLAB  语言及应用”课程教学改革与探索[J].黑龙江教育  （理论与实践），2024，78（7）：67-69.

编辑∕王力

【收稿日期】2024-04-16                                                        【修回日期】2024-07-16

【作者简介】王永娟，女，副教授，研究方向为大数据教学与实验；姚艳，女，教授，研究方向为数学教学与数学实验；范英兵，男，副教授，研究方向为数据处理与分析。

【基金项目】教育部产学合作协同育人项目“新工科背景下数据科学与大数据技术专业教师教学与实践能力提升培训”（230821263607201）；黑龙江省高等教育教学改革研究项目“新工科背景下概率论与数理统计课程混合式教学研究与实践”（SJGY20220662）