“三角形的内角和”教学设计（二）

一、理解三角形的内角和

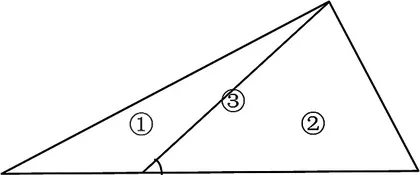
1.教师画并板书：三角形。让学生说出关于三角形掌握的知识，让学生指角。

2.教师画一条线段。现在这个图形里有几个三角形？它们的角都在哪儿？这个角是1号三角形的角吗？是3号三角形的角吗？

3.教师明确三角形的角其实是三角形的内角。（板书：内。）每个三角形中这三个内角加起来的和就是这个三角形的内角和。（板书：三角形的内角和。）请学生观察比较一下，这三个三角形内角的和哪个最大哪个最小？（设计意图：在具体的图形中明确三角形的内角、三角形的内角和的含义。）

二、动手测量计算出三角形内角和是180°

1.师板书180°和问号，提问：怎么知道这些三角形的内角和究竟是多大呢？（预设：量一量，算一算。并板书：量。）

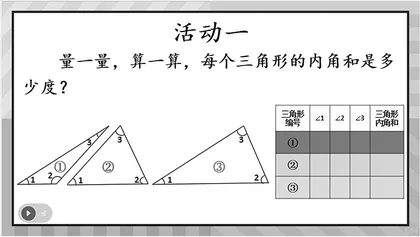
2.一号信封中有与黑板上同样的3个三角形，请学生4人一小组，合作分工，量一量，算一算，每个三角形的内角和是多少度？（完成的小组把结果进行汇总。）

3.观察学生的测量和计算数据，让学生谈发现。（预设1：这三个三角形的内角和一样大，都是180°；预设2：有的组测量的结果是179°、181°、182°、180°，不是都正好180°。）

4.教师提出有测量不够精确的情况，提问有没有其他的方法能够检验三角形的内角和到底是不是180°。

（设计意图：通过测量计算发现这三个三角形（直角三角形、锐角三角形、钝角三角形）的内角和大约都是180°，和它的大小没有关系。）

三、拼的方法、电脑验证任意三角形内角的内角和是180°

1.师预设：剪、撕、折拼成一个平角。接下来动手拼一拼，自主探索，检验三角形的内角和是180°吗？

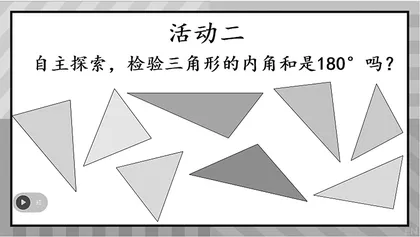
2.预设剪拼、撕拼、折拼验证出手中的三角形内角和是180°。（小结：回顾一下，我们通过多种拼角的动手操作，验证了我们手中更多的不同的三角形的内角和也都是180°。那是不是我们就可以下结论了，所有三角形的内角和都是180°呢？板书：剪、撕、折拼。）

（设计意图：小组合作通过剪、撕、折可以把三角形内角和拼成一个平角，验证三角形的内角和都是180°。）

3.打开几何画板中的一个三角形，电脑会自动计算出每个角的度数和内角和，观察现在每个角的度数是多少，内角和是多少度？老师拉动任意顶点，观察内角和的变化，让学生谈发现了什么。（预设：三角形的内角和与三角形的形状、大小都没有关系，任意三角形内角和就是180°。板书：任意，擦掉问号。）

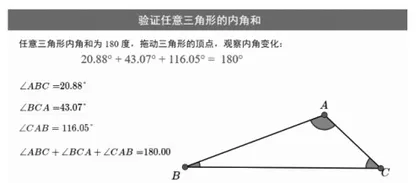
（设计意图：通过拖拽三角形的顶点发现三角形的三个角互相牵制，一个变大另外两个在变小，一个变小另外两个变大。而且三角形的大小、形状发生变化，但是三角形的内角和仍然是180°，进一步验证任意三角形的内角和都是180°。）

四、推算多边形的内角和

1.长方形的内角和是多少度？（预设1：因为长方形有4个直角，90°乘4就是360°；预设2：把这个长方形分成两个直角三角形，三角形的内角和是180°，乘2也等于360°。）

2.不规则四边形的内角和是多少度？五边形、六边形呢？（小结：这些图形都是分成几个三角形，利用的都是三角形的内角和是180°来解决的。）

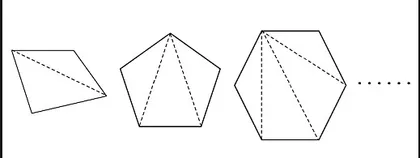
3.这是一种新的方法，推理加计算就是推算。（板书：推算。）

（设计意图：用推算的方法把多边形转化成多个三角形，应用三角形的内角和是180°解决多边形的内角和问题。）

五、应用三角形的内角和解决问题

1.这是我们课前研究过的三角形，你能根据其中几个角的度数，求出每个三角形其他角的度数吗？

求出每个三角形其他内角的度数

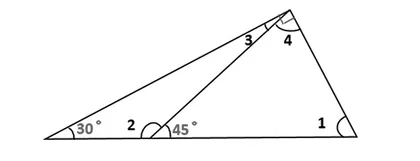
2.观察求出来的各个角的度数，它们之间有什么关系吗？你有了怎样的发现？

（设计意图：应用三角形的内角和是180°和已知条件多角度解决三角形其他内角度数问题。）

六、数学文化拓展，全课总结

教师播放数学文化视频：介绍古希腊科学家泰勒斯、毕达哥拉斯、欧几里得以及法国数学家帕斯卡研究三角形内角和的案例。