巧用问题创设，构建高效课堂

摘 要：文章结合二次函数知识在广州中考考查的价值和功能，通过巧用问题创设的方式，对二次函数核心概念的教学进行探究。以知识点为核心内容，递进式地设计一系列能够激发学生思维的问题，从而构建高效课堂。

关键词：问题创设；二次函数；教学探究；高效课堂

爱因斯坦曾经说过：“提出一个问题往往比解决一个问题更有意义。”问题创设的数学教学能基于数学知识的生长点、发展规律而设计问题，启发学生动脑思考。将数学问题融入数学教学中，教师能够利用问题创设使学生朝着既定的方向前进，当学生对问题进行回答时，教师能够及时地获取反馈，明确学生对新知识的探究情况或掌握情况，并采取措施予以指导，学生也获得更多主动参与课堂的机会，逐步建构新知，达成教学目标。

一、实战中考，剖析概念

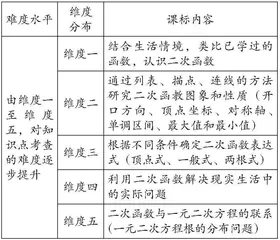
结合《义务教育数学课程标准（2022年版）》关于二次函数的学业要求，进行维度划分（如下表所示）。

通过两道广州中考真题，剖析二次函数的基础知识与考查方式。

案例1：（2021广州）抛物线y＝ax2＋bx＋c经过点（-1，0）、（3，0），且与y轴交于点（0，-5），则当x＝2时，y的值为（ ）。

A. -5    B. -3    C. -1    D. 5

案例2：（2022广州）如图，抛物线y＝ax2＋bx＋c（a≠0）的对称轴为x＝-2，下列结论正确的是（ ）。

A. a＜0

B. c＞0

C. 当x＜-2时，y随x的增大而减小

D. 当x＞-2时，y随x的增大而减小

案例剖析：从两年的中考实例分析，命题者以选择题形式围绕抛物线y＝ax2＋bx＋c（a≠0）的一般式考查学生对二次函数的图象和性质的掌握程度。题目的难度不大，以维度一和二两个层面的内容进行考查。案例2相对于案例1来说比较简单一点，以数形结合的思想方法直观得到函数相应的性质，加之在平时的教学里也经常训练到这类型的题目，所以得分率是比较高的。通过两道中考真题让学生了解考查的形式、主要考查什么内容，给教师提供研究的教学策略。

二、目标导向，巧妙设问

目标导向是基于有效教学，问题创设应该具有目标导向性。问题创设中的每一个小问题都指向一个小目标，这些小目标汇总到一起指向问题创设的总目标，由课堂中的所有问题创设以及其他教学环节共同指向本节课的教学目标。通过这样的目标传递促使教学目标的达成。在开始进行问题创设之前，要明确设计的问题需要达到怎样的目的。

基于核心概念下的二次函数一般式的概念课教学下，要明确一般式y＝ax2＋bx＋c（a≠0）由生成过程的引导，再到满足什么条件的前提下进行学习探究。在二次函数一般形式的基础上，分类讨论得出二次函数的特殊形式。建立起二次函数与一元二次方程、一次函数、正比例函数的联系。帮助学生构建知识间的联系，形成整体的学习框架，培养学生形成良好的逻辑思维。

三、顺势而为，连环追问

问题创设中的问题不是孤立存在的，它们之间存在着阶梯性、层次性，总是相互关联、相互作用影响的。通过中考真题分析，在二次函数概念课上埋下伏笔，深挖二次函数中各个维度的核心考点，借助题型和问题形式，进而根据自身学生的实际创设相应的教学问题，引导学生学习相应的知识，从而提升课堂教学质量。

（1）若m＝2，求n的值；

（2）若抛物线y＝（x－m）（x－n）与x轴交于M，N（M在N的左边），与y轴交于点G，记抛物线的顶点为E。m为何值时，点E到达最高处。

2023年的广州中考数学压轴题高屋建瓴、层层递进地考查学生对平时课堂学习效果的检测，从维度一到维度五，由简单到复杂。透过题目也能挖出二次函数概念课下的相关知识点，以二次函数的一般形式y＝ax2＋bx＋c（a≠0）为核心概念，案例3的第（2）小问正是考查学生要会把抛物线y＝（x－m）（x－n）化简为一般形式y＝（x－m）（x－n）＝x2－（m＋n）x＋mn，但又要兼顾由数到代数的能力提升。

四、融合技术，提升质量

问题创设是作用于学生的，目的是经过问题创设的引导，学生能够进行知识与经验的自主探索和建构，实现自身能力的提升和发展。以学生的最近发展区为考量、以引发学生的认知冲突为手段，在教学过程中，把问题创设下的题目结合几何画板，直观呈现函数的动态变化过程，体会函数的具体性质，加深学生在问题引领下对知识点的掌握，为学习动态数学知识做铺垫。

回顾案例3，基于中考真题深挖基础知识，利用几何画板分析带参数背景下的函数图象的变化过程，把几何画板的功能用在关键点上，把学生难以理解或者存在疑惑的关键点进行剖析，体会问题创设与知识点学习的契合。问题创设要以学生的最近发展区为论据，不能把问题过高地铺设，做到知识点与层次感分明，从而达到事半功倍的效果。以几何画板动态演示分析函数经过固定点及其图象的分布情况，为解题树立信心。

通过信息技术手段，借助几何画板动态演示函数图象的变化，可以让学生比对一下自己在训练时所画草图的准确率，从而提高后续解题的能力。因为a＝1，所以抛物线开口方向向上，并且抛物线与y轴的交点可由反比例函数值求得，所以函数顶点纵坐标最大值为-2，进而通过顶点坐标求得m的值。同样，本小问也可能通过构造新的二次函数纵坐标高时求m的值。

巧用问题创设进行课堂教学探究，教师能根据学生自身实际学情，由浅入深地把相应的知识点设置成若干个小问引导，难度逐步提升，学生畏难情绪降低，激发学生学习的热情，真正把学习的时间归还给学生。从目标导向到顺势而行，再融合信息技术进行内外剖析，借助问题创设引导学生主动学习，从而提高课堂教学质量。

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022.

［2］于宏洋．数学核心素养下的二次函数教学研究［D］.海口：海南师范大学，2020.

［3］蔡金法，姚一玲.数学“问题提出”教学的理论基础和实践研究［J］.数学教育学报，2019（04）.