基于核心概念学习进阶，发展学生科学论证能力

摘 要：文章基于概念学习进阶与科学论证整合的教学理论框架，以匀变速直线运动的位移与时间的关系为例，建构了概念学习进阶的层级假设与表现期望，设计了促进概念学习和科学论证能力协同发展的教学活动。

关键词：学习进阶；核心素养；科学论证；整合教学

《普通高中物理课程标准（2017年版2020年修订）》提出了围绕科学观念、科学思维、科学探究、科学态度与责任的物理学科核心素养目标，体现了高中物理课程“从知识为本”向“以人为本”的目标转变。这也要求物理教师在教学中要避免单一的以知识为主线，而应充分考虑到学生的认知特点与思维层次，建构学生学习进阶的路径，整合教学内容，以发展学生的学科核心素养，促进学生的全面发展。

一、概念学习进阶与科学论证整合的教学理论

弭乐、郭玉英基于“整合发展”的理念，建构了概念学习进阶与科学论证整合的教学理论框架。该框架指出，教学要依据大概念展开，以问题驱动的形式，运用口头表达、书面论证、小组合作等多种教学策略，在构建科学概念的不同进阶点时设计不同水平的论证活动，以促进学生概念理解和科学论证能力的协同发展。

结合该框架与基于学习进阶的教学设计模型展开教学设计包含四个环节：基于进阶的学情分析、学习过程的设计、教学开发、反馈。基于进阶的学情分析要根据选取的主题确定核心概念，依据核心概念和学情、教学目标分析，建构概念进阶和论证进阶框架。其中，概念进阶包含经验、映射、关联、系统、整合五个层级的表现期望，论证进阶根据表现期望分别为初级、中级、高级三种水平。学习过程的设计则是根据学生所处的概念进阶层级，结合预设的表现期望，设计相应水平的论证活动。教学开发环节应以学习过程设计为脚本，精心设计驱动问题，拟定任务流程和具体的学习活动。教学开发的活动设计是指向学生对应的表现期望。反馈是指教学实施后需要通过多种方式对学生的概念和科学论证能力发展水平进行测试和评价，帮助教师了解和掌握学生现状。下面针对人教版高中物理必修一第二章第3节“匀变速直线运动的位移与时间的关系”内容，从整合与发展的理念出发，就学情和教学目标分析、教学活动设计两个方面进行教学设计。

二、基于学习进阶的学情与教学目标分析

（一）匀变速直线运动的位移与时间的关系概念学习进阶假设

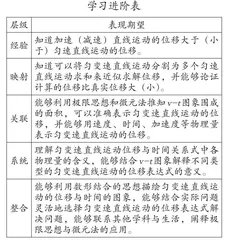
匀变速直线运动的位移与时间的关系涉及四个运动学阶段的关键概念：位移、速度、加速度、匀变速直线运动。基于科学概念理解发展层级模型，结合教学实践经验，建构匀变速直线运动的位移与时间的关系概念的学习进阶假设与具体表现期望（如下页表）。

（二）学习进阶难点分析

科学观念的形成离不开具体的物理概念和构建概念过程中蕴含的科学思想方法的支撑。在匀变速直线运动的位移与时间的关系概念建构过程中，进阶的难点在于学生并不熟悉极限思想和微元法，以及缺乏相应的数学工具和基础。教学活动应围绕主题概念，设置合适的情境，利用问题驱动，设计任务活动和学习过程，通过不同水平的论证环节帮助学生建构关键概念的进阶过程，促进概念学习进阶和科学论证能力的协同发展。

三、教学活动设计

根据学生本课内容学习过程中可能存在的进阶难点，以整合概念进阶与科学论证的能力为理念，设计本课主要的教学活动。

进阶起点：经验——匀变速直线运动图象的猜想

情境与驱动问题：展示本章第一节实验装置图，做匀变速直线运动的小车其v-t图象为一条倾斜的直线，那么其x-t图象的形状可能是什么形状？

表现期望分析：学生能够基于匀变速直线运动的速度随时间变化规律，猜测其x-t图象的形状，并能运用物理规律和数学方法进行推理和解释。

概念层级与论证水平分析：概念层级为经验层级，论证水平为初级论证水平1，即学生能够依据证据选择适当的观点。

【设计意图】利用已学实验装置设置新问题，激发学生求知热情。

进阶1：经验到映射——估算纸带上点迹的距离

回顾匀速直线运动的位移与时间关系，引导得出其v-t图象面积可以表示位移。

情境：在实验中，有一名同学不慎将原始纸带丢失，只在实验报告中找到记录下几个点瞬时速度的表格。

问题：如何估算纸带上计数点间的距离？估算的位移比真实位移偏大（小）？如何减小差值？

学生估算结束后展示丢失的原始纸带，验证估算的距离与真实距离的大小关系。

表现期望分析：在概念理解经验层级下，学生能通过将匀变速直线运动分割为多个匀速直线运动来估算位移，经过分析得出估算的位移与真实位移之间的大小关系，能够推测出如果分割的时间间隔越小，估算位移越接近真实位移。实现概念层级从经验到映射的进阶。

概念层级与论证水平分析：概念层级为映射层级，论证水平为初级论证水平2，即学生针对一个科学问题，按照要求提出观点，并用证据、理论依据、推理支持它，该过程有核心概念提示以及观点、证据、推理的提示。

【设计意图】通过学生熟悉的真实情境搭建脚手架，让学生逐步体会分割求和的微积分思想。

进阶2：映射到关联——理论推导v-t图象的面积表示位移

情境：展示匀变速直线运动的v-t图象，将其按时间等分为几个匀速直线运动。利用多媒体动画和几何画板演示将v-t图象逐渐分割的矩形面积之和逐渐逼近梯形面积的过程。

问题：这几个匀速直线运动的位移之和（矩形面积之和）能否粗略地表示匀变速直线运动的位移？如何更加精确？论证过程中用到了什么样的思想方法？你还知道哪些应用了此思想方法的例子？

展示古代割圆术的思想，介绍极限思想的应用。介绍数学上微积分思想应用以及微积分思想在生活生产实践中的应用。

表现期望分析：在概念理解为映射层级下，学生能够将匀变速直线运动的v-t图象分割为多个匀速直线运动来求和表示其位移，并能够论证如果分割的时间间隔越小，则矩形面积之和越接近真实位移。通过几何画板辅助最终得出无穷分割时，矩形面积之和等于v-t图象围成的梯形面积，能够准确反映匀变速直线运动的位移。同时，能够利用速度、加速度、时间等物理量表示出匀变速直线运动的位移，实现从概念理解映射到关联层级的进阶。

概念层级与论证水平分析：概念层级为关联层级。论证水平为中级论证水平，即学生能针对一个科学问题，按照要求提出观点，并用证据、理论依据、推理支持它，该过程没有脚手架。

【设计意图】通过本环节论证活动，使学生进一步理解极限思想与微元法的应用，联系其他学科和生活生产时间，通过真实情境整合科学知识，以发展学生的科学思维、科学态度与责任的核心素养。

进阶3：关联到系统——推导匀变速直线运动的位移表达式

问题1：如何利用速度、加速度、时间等物理量表示出梯形的面积？

问题2：有同学认为，刚才的结果是从匀加速直线运动出发推导的，对于匀减速直线运动则不成立，你的观点是？

表现期望分析：在概念理解关联层级下，学生能够运用匀变速直线运动的速度与时间变化规律、加速度以及梯形面积公式得出多种表示匀变速直线运动位移的表达式，可以结合v-t图象的面积进行数形结合的论证，能够通过反驳观点，进而理解位移表达式中速度、加速度的矢量性。实现从概念理解的关联到系统层级的进阶。

概念层级与论证水平分析：概念层级为系统层级，论证水平为高级论证水平，即学生能针对一个或几个观点，按照要求构建科学论证，包括观点、证据、推理、反驳，该过程有概念、推理、证据、反驳的提示。

【设计意图】让学生经历匀变速直线运动的位移关系式的推导过程，鼓励学生从多个角度、利用多种方式得出结论，有助于发展学生的思维品质。

进阶4：系统到整合——描绘和论证匀变速直线运动的x-t图象

情境：展示如下图①②所示的两幅学生画出的x-t图象。

问题：哪一幅图正确地反映了其位移与时间的关系？

实验验证情境：利用位移传感器验证讨论的结果。

问题：有同学认为，物体做的是直线运动，画出的x-t图象不应该是曲线，怎么解释？

表现期望分析：在概念理解的系统层级下，学生能定性描绘出匀变速直线运动的x-t图象，能运用数形结合等方法建构科学论证，指出不合理图象的错误之处，并独立提出科学观点，实现概念理解从系统到整合层级的进阶。

概念层级与论证水平分析：概念层级为整合层级，论证水平为高级论证水平，即学生能针对一个或几个观点，按照要求构建科学论证，包括观点、证据、理论依据、推理、反驳，该过程没有脚手架。

【设计意图】回扣引入时的话题，同时通过实验验证环节学生所做出的x-t图象，能够让学生经历探究成功的喜悦，同时发展学生科学探究的核心素养。

四、结语与展望

在新课程改革理念下，围绕核心概念的教学内容整合已经成为众多专家和一线教师的共识。核心概念的学习需要一系列具体概念的学习才能实现，指向概念的学习与关键能力的培养的整合教学有利于促进学生的核心素养发展。以往教学过程中，教师往往是凭借经验确定学生具有的认知水平和思维层次，并在此基础上展开教学设计。但在飞速变化的时代下，学生的变化也是巨大，以往的经验是否还依旧准确令人怀疑。通过学习进阶测试工具，可以更准确地了解学生的概念理解层级以及能力水平，进而选择更科学的教学策略。

参考文献：

［1］弭乐.郭玉英.概念学习进阶与科学论证整合的教学设计研究［J］.课程·教材·教法，2018（05）.

［2］张玉峰.基于学习进阶的科学概念教学内容整合［J］.课程·教材·教法，2019（01）.