探究基于“分解”思维的问题解决之径

摘要：本文分析了计算思维的概念，强调了“分解”思维在培养学生问题解决能力中的核心作用，阐述了分解思维在不同学段的教学目标和应用，并通过浙教版《信息科技》中的具体案例，展示了如何在教学实践中培养学生的分解思维，包括粗细相融的算法描述、降低问题规模以简化解决过程，以及分而治之的算法策略，从而达到培养学生分解思维能力的目的。

关键词：计算思维；信息科技；规模分解；行动分解；子问题

中图分类号：G434  文献标识码：A  论文编号：1674-2117（2025）07-0033-04

《义务教育信息科技课程标准（2022年版）》（以下简称“新课标”）指出：“要让学生初步具备解决问题的能力，发展计算思维。”那何为计算思维呢？新课标指出：“计算思维是指个体运用计算机科学领域的思想方法，在问题解决过程中涉及的抽象、分解、建模、算法设计等思维活动。”由此可见，分解、抽象、建模、算法设计等思维活动是计算思维的具体表现，笔者从计算思维中“分解”的角度切入，通过挖掘分解的内涵和价值，并结合浙教版《信息科技》中的内容，通过教学实践，探究小学生信息科技课程中“分解”思维的培养路径。

价值体认，挖掘“分解”之“本”

1.理论研习，探究计算思维中的“分解”

2006年，周以真教授首次明确提出了“计算思维”这一概念，她不仅明确了什么是计算思维，还指出计算思维包括递归、并行、抽象、分解等思维方法。可见，“分解”思维是计算思维的重要组成部分之一。

分解思维是计算思维的基础和核心。在计算思维中，分解是将复杂问题拆解成若干个子问题的过程，通过解决这些子问题来逐步接近最终的问题解决。分解思维有助于培养学生的逻辑思维能力和系统化思考方式，为计算思维的其他组成部分如抽象、建模和算法设计等提供有力支持。

2.分层递进，理解新课标中的“分解”

笔者通过分析新课标发现，“分解”一词共出现了15次。例如，在核心素养的内涵中，在介绍什么是“计算思维”时出现了“分解”一词；第二学段在学业要求部分指出“结合学习需要，能将问题进行分解”；计算思维第三学段目标明确指出“对于给定的任务，能将其分解为一系列的实施步骤”；在第三学段的“过程与控制”模块中，出现了“能合理选用数字化工具解决简单问题，能将问题分解”的描述；在第四学段的“互联网应用与创新”模块中，也有“互联网TCP/IP协议是如何将复杂问题一步步分层、分解，直至细化到网络设备和具体算法能处理的程度的”的描述。

由此可见，“分解”主要出现在核心素养计算思维部分，这再一次证明了分解思维是计算思维的核心之一。同时，分解一词也出现在不同学段的内容模块中，它的学习将会贯穿于整个义务教育学段之中。

3.整合体系，梳理新版教材中的“分解”

由于新课标中多处出现了分解一词，因此，在2023浙教版《信息科技》中，也有多节课涉及了相关概念。例如，三年级上册第13课《分解问题步骤》，其内容初步介绍了问题分解的方法，以及用图示画出解决问题的步骤；五年级上册第10课《问题的分解》，通过问题的界定、问题的分解、关键问题的确定等对问题进行分析，为后续进一步用算法解决问题打下基础；五年级下册第2课《系统的构成》，主要介绍了系统与子系统等内容，这也是对分解思维的精准诠释。

教材通过多节课的设计，深入浅出地介绍了分解问题的概念和方法，充分展现了分解思维在计算思维培养中的重要地位。这些教学内容不仅有助于培养学生的逻辑思维和系统化思考方式，还能为他们未来的学习和生活奠定坚实的基础。

聚焦素养，分层“分解”之“理”

1.以“分解方法”为切入点，探寻“分解”思维的应用价值

“分解”的思维方式不管在生活中还是在计算机中都很常见。常用的分解方法有规模分解和行动分解。

规模分解是指把问题分解成类似的规模更小的子问题。计算机的并行操作就是基于此分解思维，在把大问题进行分解后，计算机就可以同时处理这些类似的但规模更小的子问题。行动分解是指把问题分解成一个个可操作的子问题，即把问题按照其解决的具体步骤分解开来，把大问题变成小问题，然后逐步依次解决，这种分解的思维方法对应于计算机的串行操作，计算机依次执行各个小问题的解决过程。

在课堂教学策略方面，课堂组织活动可以包括三个方面：独立思考、组内协作和组间交流共享。在明确任务后，学生首先进行独立思考，尝试画出分解结构图。接着，小组成员之间进行交流讨论，相互对比，并形成一致意见。最后，每组代表上台展示，进行组间分享。

通过生活中的实例应用，学生不仅能够逐步掌握分解思维方式，还能为后续抽象、建模、算法设计的学习打下坚实的基础，从而更好地培养计算思维。

2.以“核心素养”为着力点，确定“分解”内容的教学目标

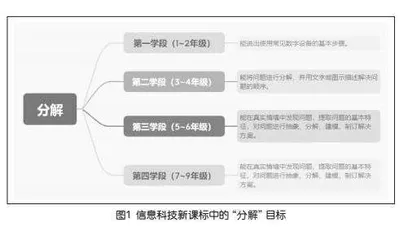
在新课标中，针对不同年段，都涉及“分解”思维培养，因此在信息科技课堂上，相应的总体教学目标为：通过学习，能够形成问题分解的意识，面对复杂问题可以对其进行合理的分解，并找到其中解决问题的关键要素。分解的思想从第一学段一直贯穿到初中的第四学段（如图1），聚焦于计算思维这一核心素养。

通过确定各学段的教学目标，教师可以有针对性地开展教学活动，确保学生在不同阶段都能得到适当的引导和训练。这样，学生不仅能够逐步掌握分解思维的方法和技巧，还能在实践中不断应用和提升这种思维方式，从而更好地培养计算思维能力和问题解决能力。

3.以“分解思维”为出发点，扩展“分解”的内涵和外延

在计算思维中，分解思维与抽象思维、建模思维等紧密相连，共同构成了计算思维的核心要素。

分解的内涵在于将复杂问题或任务进行细化、具体化，以便更好地理解和解决。通过对问题进行合理的分解，可以将大问题转化为一系列小问题，从而更容易找到解决问题的突破口和关键点。同时，分解也有助于学生更深入地理解问题的本质和内在结构，为后续的抽象、建模和算法设计提供有力支持。

分解的外延则体现在其广泛的应用领域和场景中。无论是在科学研究、工程设计领域还是在企业管理等领域中，都可以看到分解思维的身影。此外，分解思维还可以与其他思维方式相结合，形成更为强大和灵活的问题解决策略。

集智聚力，探索“分解”之“径”

“分解”的思维始终贯穿于信息科技课程的学习中，那应如何帮助学生建立起分解的思维呢？下面，笔者以浙教版《信息科技》为例，通过具体的教学实践，探究如何帮助学生更好地建立“分解”思维。

1.粗细相融，让算法描述更细化

算法的描述作为算法学习的重要组成部分，是初步学习算法的重要手段，也是算法学习的基础。通过学习算法的描述，学生可以了解和掌握算法的基本概念和方法，为将来进一步学习用算法解决问题打下基础。

在浙教版《信息科技》中，五年级上册第一单元安排了算法的描述，本单元前两课分别是《身边的算法》《自然语言描述算法》，这两课的教学目标层层递进，在用自然语言描述算法的时候，会利用到“分解”的思维。一开始，学生对算法的描述可以是相对比较粗颗粒度的，但是随着学习的深入，为了能更清晰地描述算法，需要将算法步骤进行层层分解甚至分解成接近指令级别的，可以让计算机直接处理子问题，最终逐一解决。

因此在教学策略上，可以通过尝试从使用身边的例子入手，如教材中的购票算法、课桌椅两两交换算法等，让学生理解具体算法在日常生活中的应用，引导学生学会将大问题分解成大小不同的小问题，从粗颗粒度开始，逐渐细化，直到分解成接近指令级别的子问题。然后，让学生通过实际操作，如编程、设计小游戏等，体验算法的实际应用，加深对算法的理解。同时，教师要及时收集学生的反馈，评估学生的学习进度和掌握情况，以便调整教学策略。

2.降低规模，让问题解决更便捷

在算法学习的过程中，除了通过调整颗粒度对算法描述进行细化和分解，教师还可以对问题进行规模上的分解。通过规模分解，复杂问题可以被划分为一系列规模较小但相似的子问题，这使得计算机可以采用并行处理的方式，迅速解决这些问题。

以五年级上册第10课《问题的分解》为例，本课旨在通过具体的教学实践，使学生掌握问题分解的策略。在教学中，笔者创设了“自动送货机器人在校园内送货的最优路径”的情境，这是一个真实且富有挑战性的问题。学生通过对地图路线的深入分析，发现可以通过设置路线必经点来简化问题。原本每条路线包含四个小分段，通过设置必经点，学生成功地将问题规模缩小，每条路线只包含两个小分段，从而大大简化了问题的解决过程。

在具体教学策略方面，采用三年级上册第13课《分解问题步骤》中的分解结构图形式。通过设计“任务一：行动分解”，引导学生将大问题分解成若干个可操作的小问题。学生在完成第一次分解后，成功地将原问题细化为三个子问题。

随后，进一步引入规模分解的概念，通过设置“任务二：规模分解”，指导学生将问题进一步分解为更小规模的相似子问题。在此过程中，利用填空式支架（如下页图2），帮助学生识别并确定分解的关键点。通过对比不同分解方案下的“比较次数”，学生深刻体会到分解策略在提升问题解决效率方面的优势。

经过两次分解的实践，学生不仅掌握了规模分解和行动分解的方法，还学会了如何综合运用这两种分解策略来解决复杂问题。最后，引导学生将两次分解的结果整合成一个完整的分解形式图，以便更好地理解和应用这两种分解方法。

3.分而治之，让算法策略更多元

除了对问题进行行动分解和规模分解之外，还可以延伸分解思维，应用到分治算法的学习中。“分治”除了对问题进行分解，还要能够有效地合并各个子问题的解决方案，从而顺利解决整个问题。

以五年级上册第15课《算法的应用》为例，本课旨在通过体验分治算法，认识到算法思维在生活中的应用。在教学实践中，笔者引入了一个非常经典的纸张排序问题：假设有100张无序的纸张，我们如何快速地将它们按照从小到大的顺序排列好？在教学过程中，首先引导学生对这个问题进行分解，学生可以将这100张纸张分成若干组，如每组10张。然后，对每一组纸张进行排序。这个步骤是关键，因为它将原始的大问题分解为若干个小问题，每个小问题都相对容易解决。接下来，进一步引导学生思考如何合并这些小问题。学生可以采用归并排序的思想，将两个已排序的小组合并成一个更大的已排序小组。为了使学生更好地理解这一过程，课堂上使用了10张纸牌代表100张纸张，每张纸牌上标有一个数字。首先，将这10张纸牌分成两组，每组5张，并让学生分别对这两组纸牌进行排序。然后，指导学生如何将这两个已排序的小组合并成一个更大的已排序组。通过反复练习和讨论，学生逐渐掌握了分治策略的核心思想。

通过本次教学实践，不仅让学生学会了分治策略，还进一步培养了他们的分解思维。他们意识到，在面对复杂问题时，通过合理地分解和合并子问题，可以大大提高问题解决的效率和准确性。

结语

分解思维作为计算思维的基石，是学生在信息科技课程中不可或缺的核心技能。通过精心策划的教学活动和实践环节，能够让学生逐步提升将复杂问题拆解为多个小问题的能力，并理清各小问题间的逻辑顺序，建立它们之间的联系。

参考文献：

[1]Wing J M.Computational thinking[J].Communications of the ACM，2006（03）：33-36.

[2]王荣良.让大脑成为计算模型的容器——算法、编程在计算思维教育中的作用[J].中国信息技术教育，2022（20）：35-38.

[3]范文翔，张一春，李艺.国内外计算思维研究与发展综述[J].远程教育杂志，2018（02）：3-15.

[4]张屹，陈邓康，付卫东，等.基于新课标的中小学生计算思维量表构建研究[J].电化教育研究，2024，45（03）：90-98.

[5]谢忠新，曹杨璐.中小学信息技术学科学生计算思维培养的策略与方法[J].中国电化教育，2015，346（11）：116-120.

[6]潘磊，潘以锋.基于计算思维中分解思维培养的策略探究[J].教育现代化，2020（45）：162-165.