少数民族地区数学分析课程教学内容改革与设计探索

摘  要：在坚持立德树人的目标指引下，以数学史和数学文化为载体在数学分析的课程教学设计中融入数学思想方法的讲授，加强应用创新能力的培养，淡化数学运算技巧的训练，激发学生的学习热情和厚植爱国主义情怀。基于OBE教育理念探索因材施教的教学新方法和新模式，建立基于“学生中心、能力本位”的教学模式。坚持以学生为本，调动学生自主学习的积极性，探索“互联网+”教育技术与传统的教学手段有机融合，能够体现数学分析专业基础课程特点、取长补短的教学新模式。

关键词：数学分析；课程思政；课程改革；OBE教育理念；“互联网+”教育技术

中图分类号：G642      文献标志码：A          文章编号：2096-000X（2025）08-0146-04

Abstract： In order to achieve the goal of cultivating virtue and cultivating people，  the mathematical ideas and methods is integrated into the curriculum design of Mathematical Analysis by using mathematical history and mathematical culture as carriers， strengthening the cultivation of applied innovation ability， downplaying the training of mathematical calculation skills， and stimulating students' enthusiasm for learning and cultivating patriotism. The paper exploresnew teaching methods and models based on the OBE education concept， establishesa teaching model based on "student-centered and competency oriented"， adheres to the student-centered approach， mobilizes students'enthusiasm for independent learning， and explores the organic integration of "Internet+" educational technology and traditional teaching methods， which can reflect the characteristics of the basic curriculum of Mathematical Analysis and the new teaching model of learning from each other.

Keywords： Mathematical Analysis; curriculum ideological and political education; curriculum reform; OBE education philosophy; "Internet +" educational technology

数学分析作为数学相关专业的核心专业基础课程，内容非常丰富。众所周知，专业基础课程的教学目的是传授专业知识、培养数学思维方法和应用数学解决实际问题的创新能力。传统的数学分析教学模式和教学内容已经不能完全实现对学生思维方法与创新能力的培养，因此必须进行教学改革。鉴于少数民族地区学生的数学基础薄弱、数学思维方法和创新能力的培养不足，要想培养出具有过硬专业知识、良好数学思维能力和创新能力的数学类专门人才，数学分析教学改革是十分必要的。

众所周知，教育教学、科学研究、服务社会和文化传承是现代高等教育的四大职能，高等教育的终极目的是促进人的全面发展。大学数学教育学习的目的是领会数学思想方法，提高运用数学解决实际问题的能力。鉴于数学分析的师资力量与教学水平、学生的数学基础、教学设施等主要原因，数学分析课程的教学未能满足培养具有过硬专业知识、良好数学思维能力和创新能力的数学类专门人才的要求。传统的教学方式培养的学生中多数学生仅能做到会求极限、会求导数、会算积分和会求解级数等简单的操作，不理解数学分析的思想与方法。传统的数学分析教学不能完全适应OBE教学理念和课程思政的要求，因此数学分析课程的课程内容设计和教学模式改革是很有必要的。

一  坚持立德树人，培养应用型创新人才

（一）  改革的必要性

目前，对数学基础学科的研究仍然是世界各国的重心。数学的产生和发展与人类社会紧密结合在一起，数学的发展对人类的生活、生产和科技起着巨大的推动作用。在如今经济和科技的高速发展中，几乎所有的重大科学发现都与数学密切相关。数学到底有多重要，俗话说“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学”。在国防安全、能源、信息、生物医药、航空航天、海洋、先进制造和人工智能等领域都需要数学的重要理论支撑，解决“卡脖子”问题也需要数学这样的重要科学工具。在基础学科深化建设行动背景下，为适应“十四五”发展规划及国家一流专业建设要求，对作为数学基础学科最重要的一门课程数学分析进行教学改革是非常有必要的。

（二）  改革举措

开展对数学分析教学内容、课程体系、教学方法和教学手段的改革，并将最新的教研成果和科学前沿问题逐步吸收到课堂教学中来。研究国内外经典数学分析教材，以OBE教学理念和少数民族地区大学生的数学基础为指导，合理安排理论体系，实现教学内容的更新和优化。结合专业特色和满足不同数学分支之间的相互渗透原则，对数学分析课程和内容的重组。强化数学思想与方法的系统性传授，增强数学创新思维与能力的培养，淡化微积分计算与证明技巧性训练。融入思政内容，探索数学分析课程思政的教学新模式。坚持以本为本，全面调动学生自主学习的积极性。探索“互联网+”教育技术与传统的教学手段有机融合、取长补短的教学新模式。

1  利用Baltamatica软件辅助教学，提升学生的创新能力

“北太天元数值计算通用软件”（Baltamatica软件），填补在通用型软件领域国产化科学计算软件的空白。通用型科学计算软件是开发工业软件的重要基础性工具，长期以来，通用型科学计算软件的市场全部由国外公司垄断。Baltamatica软件是由北京大学重庆大数据研究院数值计算实验室历时一年打造的科学计算通用型软件，填补了国内在此领域的空白，突破了通用型科学计算软件“卡脖子”技术难题。该软件可以用于算法开发、数据可视化、数据分析及数值计算等[1]。数学分析是普通本科高等院校数学类专业最重要的基础课程之一，大一新生普遍对该课程的高度抽象性感到很迷惑，因此利用国产科学计算Baltamatica软件辅助教学可以直观有效地化解课程中的部分难点，缩短数学理论与应用的距离，同时还能够培养学生应用数学进行创新的能力，激发学生们的爱国情怀和树立正确的科学技术精神。

2  注重数学思想与方法的培养，提升学生解决问题的能力

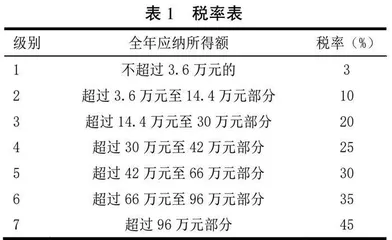
作为位于少数民族地区的少数民族高校——贵州民族大学在数学分析的课程教学团队教学过程中注重数学思想和方法传授，重点传授逼近的思想与方法、由简入繁的思想与方法和化繁为简的思想与方法等三大数学思想和方法[2]。如在讲述逼近的思想与方法的传授上，圆面积的推导可以用正多边形面积探究，当正多边形的边数越来越多时，正多边形面积接近圆的面积。这样推导圆面积，渗透的是无限逼近思想。在教学内容设计上，坚持以提升学生的能力为中心，重点培养学生们的具体问题数学化、定性描述到定量演绎、数学对象抽象体化、数学理论的推广应用和精确化数学语言的使用等能力。如在实际问题数学建模的能力培养上，讲课中以个人所得税税率表的数学化为例。税率见表1。

表1  税率表

假设全年应纳税所得额为x元，应纳税额为f（x）元，则

并以此例子教育学生每个中国公民都应尽依法纳税的义务，大学生更应该自觉树立纳税意识，做到毕业参加工作后自觉依法并诚信纳税，以主人翁的态度积极行使纳税人的权利，关注国家对税收的征管和使用，对贪污和浪费国家资财的行为进行严厉的批评并检举，最终要维护国家和人民的利益。告诉学生当你享受了社会很大的红利时，就更应该积极地履行自己的义务。

3  将数学建模思想融入数学分析课程教学的实践，提高学生的学习兴趣

将数学建模思想融入数学分析课程教学中是很有必要的[3]，但如何融入数学建模思想则要有一个合适的切入点，不能用数学建模课的内容过多占用数学分析课的教学。每个概念的引入，都经过教学团队的精心讨论。在进行数学分析教学内容讲述时，可以把数值离散化的科学计算思想渗透：①讲述定积分以及微分教学内容时，加入数值离散化的科学计算方法的讲授，使得数值积分与数值微分的数值离散化科学计算思想在学生中入心入脑。通过数学科学计算软件演示，使得学生深入理解求极限的过程。通过剖分份数的不断增加，数值算法获得的近似解就会越来越接近问题的解析解。②在讲授Taylor展开式的教学内容时，引入任意一个复杂的光滑函数的多项式逼近算法。③在讲授Fourier展开式的教学内容时，引入Fourier分析在信号处理、图像处理和物理学等中的应用实例。

通过这些实践教学，学生感受到数学分析的知识和实际问题是贴近的，从而学生就有了一种亲切感和成就感，就不再觉得数学分析特别抽象，而且扩大了学生的知识面。

4  把科学家精神融入数学分析课堂教学，培养学生科学的价值观

在20世纪中叶，中国科学家们在中国共产党的领导下撰写了新中国的高科技大文章，中国科学家们展现出了崇高精神风貌，形成“两弹一星”精神。在党中央“向科学进军”口号的鼓舞下，怀抱科技报国初心的中国科学家们掀起国家科技研究的高潮，相继取得“两弹一星”、电子计算机、人工合成牛胰岛素等重大科技成果。特别地，1973 年世界著名的哥德巴赫猜想中的“1+2”被陈景润教授证明了。即任意充分大的偶数A，都有A=B+C，其中B是奇质数，C是不超过两个奇质数的乘积。该成果被国际数学界誉为“陈氏定理”，这为我国科技现代化奠定了坚实的基础。陈景润院士的事迹在1978年以后被广为传颂，对形成尊重知识、尊重人才之风起到了重要作用，也让一大批青年学子深受鼓舞，坚定了科学报国的决心。

数学定理的推导和计算体现了科学精神、实事求是和务实精神[4]。在数学建模竞赛中锻炼学生的团队协作、协同共进的科学家精神。弘扬科学家精神，不仅有利于培养学生的科学价值观，而且有利于推进新时期社会主义现代化强国的建设。

5  坚持立德树人，实现“三全育人”

将思政元素融入到数学分析教学内容中，有利于以下目标的实现：①基于定理的证明推导详细过程讲解，培养学生具有实事求是的工作态度和良好的逻辑思维能力。②实施实际生活案例与数学分析主要知识点有机融合，提升学生分析与解决日常生活中的问题的能力。③将思政元素与数学分析抽象知识有机融合，培养学生具有多学科交叉融合的创新意识。④结合中国的传统文化，利用古今中国数学家的科学成就和生活轶事，激发爱国情怀。

将具有强烈的时代性和民族特色的数学史与数学文化有机融入数学分析课程内容教学，介绍“刘徽的割圆术”。中国古代著名数学家刘徽被视作“中国数学的牛顿”，其提出的割补术为许多数学难题提供了解决方案，如系统地证明各种图形的面积计算公式。享誉国内外的中国著名数学家吴文俊先生称刘徽的割补术为“出入相补原理”：图形在平面上由一处移至他处，其面积不变。当图形S分割成若干块，则各块面积之和等于S的面积。刘徽通过大量的计算，一直推算到了圆内接正3 072边形的周长，求得了圆周率3 927/1 250（等于3.141 6），这是当时世界上最精确的圆周率。刘徽的割圆术不仅仅是圆周率计算的精确方法及计算圆周率这么简单，更是在人类历史上首次在数学证明中引入极限和无穷小分割的思想，具有非同一般的科学意义。