三问三理：构建知识体系，落实核心素养

［摘 要］在“四边形的认识”教学中，借助前测反馈、对比辨析、特征甄别、合作验证和生活践行等方式，通过“追问——理解四边形概念内涵”“反问——理顺特殊四边形关系之网”和“辩问——理清四边形知识结构”，促进学生深度理解与建构四边形知识，凸显“三问三理”对学生数学思维发展和核心素养落实的重要意义。

［关键词］四边形；三问三理；知识建构；核心素养

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）08-0008-05

【课前思考】

在小学数学中，图形与几何领域是培养学生空间观念和逻辑思维的重要阵地。“四边形的认识”作为其中的关键内容，对学生数学素养的提升具有基础性意义。《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）指出“通过合适的主题整合教学内容，帮助学生学会用整体的、联系的、发展的眼光看问题，形成科学的思维习惯，发展核心素养”。传统教学方式有较大的局限性，难以使学生深入理解四边形知识的内在联系和本质特征。为此，本文基于《课程标准》构建“三问三理”教学策略：从边和角的角度出发，通过追问进行深入、反复的询问和探究，以梳理知识促进学生深入理解四边形概念的内涵；通过反问提出与常规思维相悖或引人深思的问题，打破固有的认知和思维定式，激发学生更全面、深入地分析、理解和理顺特殊四边形关系之网；通过辩问，引导学生辩论、质疑和探讨，提出具有批判性和思辨性的问题，理清四边形的知识结构。“三问三理”教学策略旨在帮助学生在学习“四边形的认识”的过程中构建完整且系统的四边形知识体系，发展核心素养。

【教材分析】

一、纵向分析

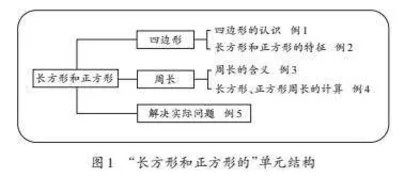
在单元视角下分析人教版教材三年级上册第七单元“长方形和正方形”。本单元具体内容结构如图1所示。

“四边形的认识”是小学阶段学生认识平面图形特征的第一课，教材的内容是从“边”和“角”两个维度研究平面图形的特征：通过认识众多图形，学生总结出四边形的特点——四条直的边和四个角；在探究长方形和正方形的特征时，依然从对边相等及角的特殊性入手，进一步分析这两种图形的特点；围绕“边”研究长方形和正方形的周长。这些安排凸显了“边”和“角”在本单元中的重要性。因此，教师需要认真把握这一课时，在“边”和“角”的教学上做好充分的准备，为学生的后续学习打下坚实的基础。

二、横向对比

横向对比不同版本教材的相关内容（如图2-1、2-2、2-3），可以发现“四边形的认识”这一课的编排各不相同。

人教版教材将“四边形的认识”编排在三年级上册“长方形和正方形”单元的第一课时，从“边”和“角”两个维度来介绍四边形，为后续的长方形和正方形教学做准备。

苏教版教材则将这一内容编排在二年级上册第二单元“平行四边形的初步认识”的第一课时。此单元主要是从“边”的维度来定义四边形，学生在认识四边形的同时也学习三角形和五边形。

北师大版教材在四年级下册第二单元“认识三角形和四边形”的第一课时“图形分类”中编排了“四边形的认识”，主要也是从“边”的维度来区分三角形和四边形。

对比三个版本的教材后可以看出，只有人教版教材从“边”和“角”两个维度来介绍四边形，并且随后从这两个维度探讨长方形和正方形的特征，为后续的周长计算及应用教学做好了铺垫。

【学情分析】

学生对本节课的认识有哪些？困难点在哪里？这节课的增量又在哪里？在学习本课之前，学生已经掌握了一定的图形与几何的知识（如图3），学生对长方形、正方形、平行四边形和梯形等特殊四边形已有初步认识，且这些图形在他们心中是四边形的代表。但在几次试教和前测中发现，部分学生认为四边形只有长方形、正方形、平行四边形和梯形，即四边形仅包括这些常见的特殊四边形。显然，他们对不常见的常规四边形较为陌生。

然而，这些不常见的常规四边形可以通过“边”和“角”的变化与特殊四边形建立联系，从而更好地激发学生的空间想象能力。于是，笔者确定了教学目标：

目标1.直观感知四边形，认识四边形的特点，能利用四边形的特点区分和辨认四边形，进一步认识长方形和正方形。

目标2.经历猜想和验证，在量、折、比等活动中验证长方形和正方形的边和角特征，提升观察、比较和概括抽象的能力。

目标3.通过“猜一猜”的活动，感受不同四边形之间的联系与差异，理解边与角的变换可以实现它们的相互转化，并通过图片和生活中的实例体会四边形在生活中的普遍性，形成将数学知识应用于生活的意识。

在深入剖析教材与精准把握学情后，教师能够清晰地洞察到“四边形的认识”教学中的关键要点与学生的实际需求。“三问三理”教学策略恰似一把精准适配的钥匙，能够巧妙开启深入理解四边形知识的大门，优化教学效果，并有效培育学生的核心素养。

“三问三理”教学策略与“四边形的认识”教学的紧密对应关系和有序实施步骤（如图4），使得每个教学策略环节与教学过程紧密结合，共同推动学生对四边形知识的深入理解和系统构建。

【课堂实践】

一、追问——理解四边形概念内涵

（一）前测反馈，开启追问之门

师（出示图5）：从边和角的角度观察这些形状、大小各异的图形，有什么问题想问吗？

生1：这些图形形状、大小都不一样，为什么都叫作四边形？

生2：为什么要从边和角的角度观察？

生3：我发现它们都有四条边。

生4：它们的边都是直的。

生5：每个图形都有四个角。

本环节通过具象图形激发学生自主探究，紧扣《课程标准》对学生直观感知与观察能力的培养要求。学生从“边”与“角”两个维度初步归纳出四边形的共性——四条直边构成封闭图形并形成四个角，为后续概念建构奠定认知基础。

（二）对比辨析，深入追问本质

师（出示图6）：只有四边形可以参加“图形派对”。这些图形中，哪些可以参加？说出被淘汰图形不符合要求的原因。

师：有人认定①②③⑤⑥⑧⑩号图形均为四边形，大家同意吗？

生1：⑫号图形为什么不是四边形？

生2：四边形必须为平面图形，该图形属于立体图形。

生3：④号图形为什么不是四边形？

生4：它是不封闭的图形。四边形必须是一个封闭的平面图形。

教师通过对比正反例，引导学生聚焦概念本质属性：四边形是具有四条直边、四个角且各边首尾相连的平面图形。此过程排除非本质干扰，深化学生对概念内涵的理解，促进学生数学思维与核心素养的同步发展。

（三）特征甄别，延续追问拓展

师（出示图7）：⑬号图形收到了“图形派对”的邀请函，却被守卫拦下。守卫的做法对吗？

生1（描边数角）：该图形有四条直边、四个角且为封闭平面图形，所以它是四边形。守卫的做法不对。

师：这类特殊四边形被称为凹四边形。

此环节通过具象案例拓展概念外延，引导学生运用已有知识进行逻辑推理，深化对四边形多样性结构的认知。这样既落实《课程标准》对学生逻辑推理能力的要求，又构建起完整的四边形概念体系，实现知识建构与核心素养培育的双重目标。

二、反问—理顺特殊四边形关系之网

（一）引发思考，抛出反问引导

师：除已知边角特征外，还需研究哪些特性？

生1：我们已经知道了长方形一些边和角的特点，还有哪些是我们不知道的？

师：这是个好问题，真是爱动脑的好孩子！

生2：是否对边长度相等？

生3：四个角是否均为直角？

这一系列问答与猜想成功搭建了探究阶梯，为系统剖析图形特征做好了铺垫。

（二）合作验证，借助反问深化

师：大家的猜想是否正确？如何验证？

生1：利用刻度尺去量边的长度来比较是否相等。

生2：可以通过对折验证对边是否重合。

生3：用三角板上的直角去比一比四个角的大小。

师：同桌合作探究。

在教师指导下，学生通过量、折、比完成验证，并由此得出结论——长方形对边相等、四个角均是直角，通过辨析明确长与宽的相对定义。在此过程中，学生的数学思维得以锤炼，为探究正方形特征积累经验。

（三）观察比较，利用反问明确关系

师：知道了长方形和正方形特征，接下来要研究什么？

生1：长方形和正方形的特征有何异同？

生2：正方形的四条边都相等，长方形只是对边相等，这是它们边的不同点；但是它们的角都是直角，这是相同点。

生3：我觉得正方形其实可以看作是一种特殊的长方形，因为它不仅满足长方形对边相等的特征，而且四边相等。

通过递进式追问，学生自主构建知识体系：正方形作为长方形的特例，既满足“四边形+直角+对边相等”的普适条件，又满足“四边等长”的附加约束。该过程既强化了学生对图形特征的系统性认知，又培养了学生从一般到特殊的辩证思维能力。教师可以适时引入维恩图展示包含关系，直观呈现两类图形的逻辑层级，为学生的集合思想启蒙埋下伏笔。

三、辩问—理清四边形的知识结构

（一）猜谜游戏，开展辩问互动

师（出示装有图形的信封）：信封里面的图形的四条边相等。猜猜是什么图形。

生1：可能是正方形，因为正方形的四条边相等。长方形一般是对边相等，不符合这个条件。

师（露出图形的两个角）：这两个角是直角。

生2：是正方形。因为正方形本身就有四个直角，现在露出两个直角，很有可能就是正方形。

生3：四边形的边和角只要有一点变化，图形就不一样了。

生4：什么在变？什么不变呢？

生5：边的长度在变，但是四边形都有四条边这一点没有变。

生6：角的大小在变，但是四边形都有四个角这个本质没有变。

生7：不同的边和角组合就形成不同的四边形。

通过递进式辩问，学生揭示了图形变换的“变与不变”规律：四边形本质属性（四边、四角）恒定，非本质特征（边长、角度）可变。这个过程既深化概念认知，又渗透数学思想方法。

（二）生活应用，回归辩问本质

师（出示生活中四边形物品的图片）：看到这些图片，你能提出什么问题？

生1：这些四边形在生活中有什么作用？与数学知识有什么联系？

生2：窗户是长方形的，它的对边相等，这样安装起来比较方便，也比较美观。

生3：地砖是正方形的。正方形的四条边相等，这样在铺设地面的时候可以保证每一块地砖的大小和形状都一样，拼接起来更加整齐。

通过对具体案例的思辨讨论，学生建立了数学知识与现实世界的联结，理解四边形特征在实践中的具体体现，实现“抽象概念—具象应用—理性认知”的思维跃迁。

【课后反思】

问题是教学的载体，优化问题设计能够使学生的学习更具目标导向性和探究深度。教师通过精准提问与科学追问，促进学生思维的连贯性与整体性建构，推动学生深度学习的发生，为课堂教学质量提升提供有效支点。

一、精准之问：构建趣味化学习路径

在四边形特征前测反馈环节，创设“图形派对”主题情境，设计系列递进式问题链：“说出被淘汰图形不符合要求的原因”“⑬号图形收到了‘图形派对’的邀请函，却被守卫拦下。守卫的做法对吗？”等。通过具象化场景与儿童化语言的双重驱动，激发学生的探究兴趣，引导学生循着问题脉络追溯知识本源，为知识体系建构奠定基础。

二、互动之问：深化概念认知层次

基于四边形概念的核心地位，教学从“边”与“角”两个维度切入，通过自主质疑与探究对话推进课堂进程。在长方形特征验证环节，学生围绕“测量边长的精准方法”“对折观察对边重合的技巧”等问题展开互问互答。这种动态生成的问答过程既揭示图形属性转化规律，又渗透数学思想方法，使学生直观感受四边形的可变形特性，进而建立特殊四边形间的逻辑关联网络。

三、科学之问：完善知识体系架构

教学遵循“一般到特殊”的认知规律，以三年级学生已有知识经验为基础，设置层级递进的探究序列。当学生提出长方形与正方形存在哪些特殊性质，以及它们与其他四边形有何本质联系等问题时，教师引导学生通过边角变换的动态分析，把握图形间的包含关系与转化规律。这种系统化的思维训练，能助力学生构建层次分明的四边形知识框架，实现核心素养的有效培育。

在《课程标准》理念引领下，“三问三理”教学策略通过追问、反问、辩问的多元互动，促使学生在问题探究中完成知识建构与思维升级。教师应持续强化问题导向的教学设计能力，为学生创造自主探究的思维场域，为其终身学习发展奠定坚实基础。

［ 参 考 文 献 ］

［1］ 何霞.准确提问  适时追问：“余数要比除数小”教学引发的思考[J].中小学数学，2016（3）：56-58.

［2］ 王琳.精准分析，突破认知偏差：《四边形的认识》教学思考[J].教育视界，2022（11）：29-31.

［3］ 杨国钢.提问有追踪  思维见深度：深度追问在小学数学课堂的应用探究[J].天津教育，2021（27）：60-61.

【本文系2024年杭州市基础教研规划课题“三问三理：深度学习视域下小学数学课堂自问的策略研究”（立项编号L2024153）的阶段性成果之一。】

（责编    金    铃）