整体架构，凸显运算一致性

［摘 要］口算是数与代数领域中“数与运算”的重要内容，是学生必须掌握的一项技能。文章以“除数是一位数的口算除法”教学为例，通过“深度解读教材，提炼核心问题”“基于学情，整体架构教学”“凸显结构化教学，帮助学生领悟运算一致性”的策略，培养学生的数学核心素养。

［关键词］口算除法；运算一致性；结构化

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）08-0047-03

在传统的小学数学课堂教学中，部分教师为落实某一课的教学目标，往往能做到“三多”，即情境多、问题多、练习多。然而，教学中存在情境零散、追问不到位、信息碎片化、思考浅层次、缺乏整体意识、缺乏结构化观念等问题，导致学生很难主动地将新知与其认知结构中的旧知联系起来，也就谈不上有意义的学习。有意义的学习是指学习者头脑中的某种认知结构在吸收新的信息后进一步完善，使得原有认知得到进阶。《义务教育数学课程标准（2022年版）》提出，感悟数的运算及运算之间的关系，体会数的运算本质上的一致性，形成运算能力和推理意识。这就要求教师要注重运算一致性。

基于以上认识，笔者认为，教师应基于学情，通过整合教材内容开展结构化教学，促进学生领悟运算一致性。下面，笔者将以“除数是一位数的口算除法”教学为例，从三个方面谈谈自己的思考。

一、深度解读教材，提炼核心问题

学生在二年级下册学习了表内除法、有余数除法，在三年级下册开始学习除数是一位数的口算除法。这节课是“除数是一位数的除法”单元的“种子课”，属于数与代数领域，在学生学习整数除法的第二阶段起到承上启下的作用，为学生进一步学习除数是多位数的除法打下基础。

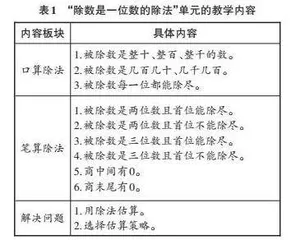
教材中将“除数是一位数的除法”单元的内容按口算除法、笔算除法、解决问题的顺序分三个层次编排，这体现了由简到繁、由易到难的学习规律（见表1）。

第一个层次是口算除法，教材编排了3道例题，分别为整十、整百、整千数除以一位数的口算，几百几十、几千几百除以一位数的口算，几十几除以一位数的口算。学生用已掌握的口算方法解决新问题，为学习本单元后续的笔算除法、解决问题奠定基础。在探究口算算理的过程中，教师应引导学生在直观的操作过程中归纳口算方法，并助力学生理解算理、沟通算法，从而使学生实现被除数从两位数到三位数、整十数到整百数、整十数到非整十数的迁移。

数与运算的内核是计数单位，数的概念是基于计数单位的“组装数”，数的运算是基于计数单位的“分解数”。因此，“除数是一位数的口算除法”这节课的关键是“如何借助几何直观，从计数单位的视角沟通算理与算法的联系”。

二、前测定位学情，立足现实起点

前测为课堂教学提供了依据。口算是学生后续学习笔算和估算的基础，也是运算教学的重点。为了更好地了解学生学习“除数是一位数的口算除法”的起点，笔者在教学前随机选取35名学生进行了前测，前测单如图1所示。

对于“60÷3”这个算式，只有4人能从数的组成和除法的意义来理解，能把60看成6个十。因此，本节课的重点应放在引导学生从计数单位的角度理解算理。此外，学生在解释“120÷3”和“36÷3”的算理时，会用到“60÷3”的算理，因此教学时可将原有的3道例题合为1课时进行教学，并把例1整合进去。

三、凸显结构教学，领悟运算本质

（一）从图形走向数字，加强数学理解

教学过程中教师要处理好算理与算法的关系，做到寓理于算，理法相融。一些教师过于强调算法，而忽略算理，如此，学生虽理解了算法，但出现变式时却不能应用自如。因此，在口算的教学过程中，教师要利用教材提供的图片、小棒、计数器等教学资源，数形结合，让学生动手操作，调动多种感官参与，以多元化的表征形式，化抽象为形象，从图形走向数字，更好地理解数的概念和运算的本质，以及二者之间关联，进而理解算理。

笔者认为教师应该在活动中帮助学生构建除法的数学模型并进行推广，让学生感受除法实际上是将被除数转化为若干个计数单位，然后运用表内除法的知识对计数单位进行均分。对于整十数、整百数或整千数除以一位数的口算，可以利用计数器表征，即用1颗珠子表示1个十、1个百或1个千，可见几个十、几个百和几个千的均分都是相同的，只是计数单位变了而已，由此，学生能建立对口算除法的意义的理解。看似简约的过程，却联系了之前所学的简单口算，这也为日后学习更多数位的口算除法建立了联系。笔者在学生弄清楚“60÷3”“600÷3”“6000÷3”都是将6个计数单位平均分成3份后，再一次用计数器展示平均分的过程，让学生进行对比（如图2）。

运算的本质是推理，推理是抽象的计算。通过数形结合的方式让学生再次从图形走向计算背后的算理，让学生感受到除法计算就是对计数单位进行均分，也能促使学生应用类比推理思想，从而让学生自主建构结构化认知。

（二）从结果走向过程，关联深度思维

口算是学生接触的众多运算中最常见的一种，也是学生最先接触的简单计算。在计算学习中，笔者对比各版本教材，发现在内容编排上都是先学习口算，再学习笔算。笔算相对复杂，是多次口算的程序化表达。除法的笔算过程就是多次乘法口算和减法口算的程序化表达的过程。熟练掌握整数乘、除法口算的关键是将算式转化为表内除法。教学时应从结果走向过程，用系统的观点、结构化的思想来构思教学过程，渗透方法，关联深度思维，让学生在学习知识的过程中逐渐形成结构化思维。

“除数是一位数的口算除法”中的“整十数、整百数、整千数除以一位数的口算除法”“几百几十除以一位数”“几十几除以一位数的口算除法”，本质都是将算式转化为表内除法。因此在教学时，教师通过一系列比较，加强新旧知识的联系，强调数学知识的迁移，让学生在理解算理的基础上概括算法，找到除数是一位数的口算除法的本质，从而提升分类、比较、概括能力。

笔者用多元表征激活学生的前期经验，进行算理的前置联构。例如，对于“66÷3”的先分后合的计算过程，学生想到了不同的表征办法——画图、摆小棒、使用计数器等，由表层至内涵，学生各抒己见，在思辨中逐渐归向本质的理解。明白“66÷3”的算理之后，笔者引导学生计算“666÷3”“66666÷3”。学生在对比关联中再次深化对除法模型的认识，进一步领会除法运算的一致性。

结构化教学能够帮助学生关注不同阶段学习的知识之间的显性联系，而且有助于学生挖掘知识背后的思想方法。教师在教学中要有意识地将知识与思想方法进行深度关联，帮助学生联结知识板块，形成结构化思维方式，使得核心素养培养落地。

（三）从不能整除走向整除，凸显数学本质

在教学中，教师应该有整体意识，即眼中不仅要有本节课的“小树”，还要有整个单元的“小树林”。“除数是一位数的口算除法”是学生后续学习笔算除法的基础，学生对除法模型的理解将影响学生对笔算除法算法的掌握。因此，在“除数是一位数的口算除法”这节课的教学中，教师应突破教材布局的局限，加入“计数单位一次分不完”的情形，让学生经历从不能整除走向整除，凸显除法模型的本质。

对于“被除数是两位数的口算”，大部分学生能够将被除数“拆开”来计算，但受加减法竖式计算的影响，部分学生习惯从低位算起，导致计算结果出错。这种负迁移不是一下子就能纠正的，因此这便成了一个教学难点。计算66÷3时，学生认为从个位算起或从高位算起都可以得出结果，对此，教师不管从分小棒的习惯来解释，即告诉学生“一般都是分完大捆再分小捆”，还是直接告诉学生从高位算起是计算法则，都缺乏说服力，使得学生对“从高位算起”的理解不够深刻。因此，笔者在练习环节中加入练习（如图3），帮助学生在均分计数单位的过程中理解为何要从高位算起。

当百位是5，算式为548÷2。如果从高位分起，则先把百位的5个百平均分成2份，每份为2个百，余1个百；把余下的1个百转化为10个十，与十位的4个十合起来为14个十，再将其平均分成2份，每份为7个十；把个位的8个一平均分成2份，每份为4个一。如果从低位分起，则先把个位的8个一平均分成2份，每份为4个一；把十位的4个十平均分成2份，每份为2个十；把5个百平均分成2份，每份为2个百，余下1个百，此时无法再接着分，余数又比除数大，这不符合除法定理。因此，从低位算起是不合理的。

对比从高位算起和从低位算起的计算步骤，学生在操作与计算中感受到从高位算起的合理性，从而深刻掌握除法计算的算理。学生有了本节课这样拆分小方块的经验，去学习“除数是一位数的笔算除法”就顺理成章了。

在教学中，教师应该从教材和学情出发，整体架构，凸显数学本质。今日的教是为了以后的少教或不教。对于“除数是一位数的口算除法”，教师应紧扣计数单位，从图形走向数字，数形结合，帮助学生感悟运算一致性；从结果走向过程，关联深度思维，进一步领悟运算一致性；从不能整除走向整除，凸显除法的本质，感悟运算一致性，最终实现核心素养培养落地。

［ 参 考 文 献 ］

[1] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[2] 许卫兵.小学数学整体建构教学[M].上海：上海教育出版社，2021.

[3] 王岩，逄亚楠，王均杰.单元整合重关联主题统整落素养：大概念下“小数乘、除法”单元设计与实践[J].小学数学教育，2021（Z3）：13-17.

[4] 史叶锋.主题式学习：从课堂走向未来[J].江苏教育研究，2016（14）：55-58.

（责编    杨偲培）