重整·重构·重建：指向深度学习的单元整合教学研究

［摘 要］倍数学习是第三学段教学的重点，其中3的倍数的特征对小学生来说较难理解。为此，教师可采用单元整合的方法进行教学。文章通过原因剖析，在读懂学生和教材的基础上对倍数特征教学中的单元内容、单元目标、单元材料和教学策略进行了单元整合的实践与思考，基于单元整合指向学生深度学习，培养学生的核心素养。

［关键词］深度学习；单元整合；教学研究；倍数特征

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）08-0050-04

一、缘起——课堂现象中的困惑

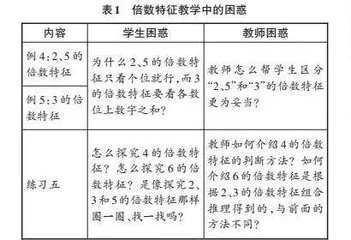
数学的学习伴随着师生间思维火花的迸射，是有趣的数学智慧的生成之旅。但在实际教学中，疑惑是客观存在的。如果这些疑惑无法妥善处理，就会导致教师教得不够清晰，学生也无法深刻学习。长此以往，学生的学习就没有活力。为此，笔者搜集了苏教版教材五年级下册第三单元“因数与倍数”的倍数特征教学中的一些师生困惑（见表1）。

面对上述困惑，教师不应忽视或回避，否则会对学生数学思维能力的提升形成阻碍。那么，教师如何在规定的教学时间内解决这些困惑呢？

二、前测——调查剖析后的感悟

要想解决困惑，最好的方法是研究教材、研究教师的教学行为和研究学生的学习障碍。

（一）教材更多关注区域差异性

教材利用“百数表”，让学生圈一圈、找一找，引导学生发现2、3和5的倍数特征，这当然是可行的。但这只能让学生对2、3和5的倍数特征进行浅层理解，并不能让学生对知识本质进行深度理解。对此，教师可以尝试引导学生开展深入知识本质的探究学习，从而培养学生的理性精神。

（二）教师可能忽略了本体性知识

“倍数特征”属于数论的范畴，离小学生的生活较远，也较为抽象。因此，教师可以尝试提供合适的学习材料，结合具体实例展开教学。如通过提供结构化方格模型，以理解2、5的倍数特征为基础，整体感知倍数特征的本质。

（三）学生缺少对知识的深度理解

笔者对本校4个班的学生进行了“3的倍数特征”的前测（如图1），测试结果见表2。

对于3的倍数特征，受2、5的倍数特征的干扰，有32%的学生还是会依据个位上的数去判断，但有50%的学生已经会用“整除”或“个位上数字之和是3的倍数”去判断了，这说明学生对3的倍数特征有了一定的理解。当2、5的倍数特征与3的倍数特征的判断方法不同时，学生自然会有困惑，为了解决学生的困惑，就要让学生经历探究、发现、总结的完整过程。因此，教师应有意识地引导学生从同一维度理解倍数特征的内在关联，让学生学会探究倍数特征的一般方法，把2、3和5的倍数特征研究透，并将探究思路和方法迁移到另一些数的倍数特征的判断上。

三、整合——单元视角下的实践

笔者对倍数特征的探究进行单元整合教学，将本单元的知识内容、单元目标和学习素材等要素进行梳理和重整，从而更精准地确立单元教学目标。

（一）内容重整

将倍数特征知识进行逻辑分类：“2、5的倍数特征”和“3的倍数特征”为“种子课”；“4、6、9、10、25的倍数特征”为“生长课”。根据学情调整“种子课”和“生长课”的学习序列。

1.调整“种子课”学习序列

教材将“3的倍数特征”安排在“4的倍数特征”之前，这符合知识由易到难的逻辑关系和学生的认知规律。那么，如果先学“4的倍数特征”是否也符合呢？学生学了“2、5的倍数特征”，理解了只看个位就能判断的方法后，接着学“4的倍数特征”，进一步理解了“个位为0、4、8时，十位上为偶数；个位为2、6时，十位上为奇数”的数就是4的倍数。同类型、同方法的探究，正是数学活动的一种经验积累，能更好地促进相关数学知识的建构。

2.整合“生长课”学习序列

调整“种子课”的学习顺序后，对“生长课”进行穿插整合。

（1）4、25的倍数特征与2、5的倍数特征在形式上紧密联系，且对2、5的倍数特征知识有巩固作用，可定为“生长课”，安排在3的倍数特征之前，2、5的倍数特征之后，独立设置一个课时。

（2）9的倍数特征与3的倍数特征在形式上紧密联系，故而整合为一个课时。6的倍数特征、10的倍数特征在此基础上进行组合探究，也合并为一个课时。至此，最终形成的课时序列见表3。

（二）目标重构

《义务教育数学课程标准（2022年版）》中对倍数特征的内容要求和学业要求表述为：知道2、3、5的倍数的特征，了解公倍数和最小公倍数，了解公因数和最大公因数；能找出2、3、5的倍数，在1～100的自然数中能找出10以内自然数的所有倍数以及10以内两个自然数的公倍数和最小公倍数。

笔者将倍数特征相关的前后知识点进行整理和分析归纳，并以此为据完善本单元的整体学习目标：1.在已有经验上研究5的倍数特征，梳理“小范围发现猜想—大范围举例验证—归纳概括”的方法结构；2.借助已有研究方法，迁移类推4、25的倍数特征，能准确判断4、25的倍数；3.用倍数特征规律探索3、9的倍数特征，能准确判断3、9的倍数，了解知识间的前后联系。

（三）材料重建

百数表是倍数特征探究中常用的学习材料，但仅靠观察百数表，3的倍数特征仍较难发现。为实现探究效果最优化，教师可根据实际需要增加必要的结构化学习材料。

以上材料，特别是结构化的位值方格图，有利于学生把与“数”对应的“形”找出来，在几何直观中探究3的倍数特征的数学本质，并类推到其他数的倍数特征学习中，明确地学数学。

（四）策略调整

单元整合教学的目的是通过重构教学目标，设立有序的教学课时，真正提升教学效率。但要达成这个目标，教师需要运用一定的策略，将思考所得付诸教学实践，并在实践中反思与修正教学想法。

1.在结构化材料中自主探寻，触摸内在本质

波利亚认为，学习任何知识的最佳途径都是由自己去发现的，因为这种发现理解最深刻，也最容易掌握其中的内在规律、性质和联系。从数学本质的角度考虑，通过自主观察、猜想验证、初步归纳3的倍数特征的规律后，进一步引导学生思考“为什么”，当学生提出“为什么3的倍数不能只看个位，而要看各数位上数字之和？”的问题时，教师可以12为例，借助方格图进行引导（如图2）。

本节课教学的重点在过程性目标上，聚焦3的倍数特征的原理。教师结合12、42、76等具体实例，通过画图支撑、自主表达、表象说理，让学生初步体会一个数各位上数字之和除以3后跟余数之间的联系。学生通过独立思考、合作交流、举例分析等多种方式进行推理论证，逐步明确判断3的倍数的方法。

2.在数形结合中建立联系，深化内在本质

数学理解的本质是学生能形成有关数学知识的网络，这与知识联系的数量、强度有关。

【教学片段】

师：看一个数是不是3的倍数，只要看各数位上数字之和是不是3的倍数。现在你还有疑惑吗？

生1：这种方法能用在三位数、四位数上吗？

师：让我们继续研究，请你任选一个三位数和一个四位数，用你喜欢的方法思考。

（学生自主活动）

师：谁愿意和大家分享你的思考成果？

（学生答略）

师：是的，老师请来了个位、十位、百位和千位的计数单位，还整理了各计数单位去掉相应的0后余下的数字，仔细观察，你有什么发现？

教师启发学生联系计数单位和位值原则对3的倍数特征进行深入探究，进一步感悟3的倍数特征所具备的结构性原理。将数论中整除、同余的原理转换成适合学生年龄特征、易于学生理解的表征形式，让学生感悟“一个数各个数位上数字之和是3的倍数，这个数就是3的倍数”的原理。

3.在有效引导下构建序列，活化内在本质

从数学知识的本质出发，教师应帮助学生铺设更为合适的探索研究空间，把倍数特征的探究放在更为宽广的数学背景中思考，可实现更好的教学效果。

【教学片段】

师：研究了3的倍数特征后，你还有疑惑吗？你还想研究哪些数的倍数特征？

生1：我想研究6的倍数特征。

师：为什么？

生1：因为6是3的2倍。它的倍数特征会不会与3有关联？

师：有道理。6既是2的倍数又是3的倍数，它的倍数特征还可能与几有关？我们可以怎么找？

生2：可以在2的倍数里找3的倍数，也可以在3的倍数里找2的倍数。

师：好方法！请大家马上试试。

利用有效的学习材料，找准倍数特征的内在逻辑，把2、3、5倍数特征的探究方法迁移推广到其他数的倍数特征的研究中，让学生学会倍数特征探究的一般方法，初步实现了以一节课来探讨一类课的目的。学生结合“种子课”的倍数特征的探究，既学会2、3、5倍数特征的推理方法，同时又能组合推理出6、10的倍数特征。

通过思考与实践，笔者发现单元视角下的整合教学是有法可循的，采用单元整合的方法能更好地提高教学效率。而作为一线教师，我们更应扎根课程标准，找准数学知识点之间的联系，建立既能提升学生学习、又能优化教师教学的知识体系，合理地构建教学内容和教学素材，并在实际教学中不断实践优化，从而指向学生的深度学习，培养学生的核心素养。

［ 参 考 文 献 ］

［1］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022.

［2］ 罗鸣亮.做一个讲道理的数学教师［M］.上海：华东师范大学出版社，2016.

［3］ 叶婉贞.探究2、3、5倍数特征的奥秘［J].中小学数学（小学版），2018（11）：38-39.

［4］ 匡金龙.聚焦数学本质   促进数学理解［J］.教育研究与评论（小学教育教学），2014（6）：5-8.

（责编    李琪琦）