有形·无形：指向深度学习的单元整合教学策略研究

［摘 要］圆柱与圆锥作为小学阶段最后系统学习的立体图形，是“图形与几何”领域的重要内容。本研究基于单元整体教学目标重构学习序列，开发“制作圆柱和圆锥”实践课程。以“图纸”为教学主线，通过“设计平面图纸—制作立体模型”和“变换平面图形—绘制立体图纸”两大模块，深度探究圆柱与圆锥的表面积及体积特征，着力培养学生空间观念、数学素养和实践能力。

［关键词］圆柱和圆锥；单元整合教学；深度学习

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）08-0063-03

小学数学教材采用单元化编排体系，各单元新知按认知逻辑有序分布，旨在帮助学生建构完整的认知结构。本文从单元整体设计视角审视课时安排，通过重构学习序列实现“整体大于部分之和”的教学效益；基于单元目标完善课时目标，达成“源于目标而高于目标”的教学定位。

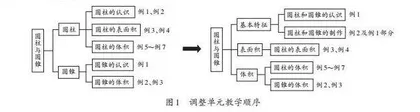
以人教版教材六年级下册“圆柱与圆锥”单元为例，本研究立足深度学习理念，对原有教学序列进行结构性调整（如图1）。调整后的教学序列突破传统教学模式，采用“基本特征→表面积→体积”的互动教学路径，强化知识间的对比联系。

一、设计平面图纸，制作立体图形——从“无形”到“有形”

陶行知曾指出：“中国教育革命的对策是手脑联盟，结果是手与脑的力量都可以大到不可思议。”在教学中，通过平面图形与立体图形的相互转化活动，可有效落实这一教育理念

（一）牛刀小试：分解一模仿一合成，再认圆柱

1.初探展开图，化“曲”为“直”

采用“想象—操作—验证”三部曲开展教学：准备三个纸模圆柱，引导学生沿母线剪裁。通过对比不同展开方式使学生感受到所有曲面展开图均可转化为矩形，直观呈现“化曲为直”的数学思想。

【教学片段1】

师：沿不同路径剪裁侧面时，展开图形状如何变化？

生1：沿高剪，得矩形。（如图2-1）

生2：沿斜线剪，得平行四边形。（如图2-2）

生3：沿曲线剪，得不规则图形。（如图2-3）

通过动手操作将抽象概念具象化，使学生直观感知圆柱体结构。这种自主探索过程实现了曲面到平面的几何转化，使“化曲为直”的数学思想在实践活动中自然生成。

2.拟画设计图，组“面”成“体”

从立体图形到平面图形的分解是训练学生的顺向思维，而通过平面图形重构立体模型则培养学生的逆向思维。教学中以核心问题驱动探究：首先以问题“任意两个圆与矩形能否组合成圆柱？”引发学生讨论；继而提出“当侧面展开图为正方形时如何设计？”深化学生思考。学生在制作圆柱模型的过程中，通过观察“高矮胖瘦”差异与对比表格数据，最终揭示规律：底面半径决定截面大小（“胖瘦”），高度决定柱体长度（“高矮”）。这一过程不仅直观呈现表面积计算原理，更在具象操作中建立平面与立体的空间对应关系。

（二）渐入佳境：猜测—验证—发现，续学圆锥

1.想象展开图，迁移转化

学生在掌握圆柱展开图的学习经验后，研究圆锥展开图便渐入佳境。教学时教师先引导学生展开合理想象，当扇形的意象浮现后，再让学生动手绘制图形，实现知识的正向迁移。

【教学片段2】

师：一个圆锥由哪几部分组成？

生1：一个圆形底面和一个侧面，侧面是曲面。

师：圆柱的侧面展开图是长方形。想象一下，圆锥的侧面展开图可能是什么形状？

生2：可能是扇形。

师：请在纸上任意画一个扇形。扇形由哪几部分组成？

生3：圆心角、半径和弧。

师：扇形的哪个部分与圆锥底面相关？

生4：扇形的弧长是底面的周长。

师：为什么？

生5：因为这条弧必须与底面周长重合才能围成圆锥。

任何新知识的学习，都是对原有知识进行迁移、转化和发展的过程，圆锥的学习亦遵循这一规律。

2.演算关联量，类比推理

未经验证的猜测仅是“假设”，唯有通过实践检验才能确认其正确性。因此，需验证“圆锥侧面展开图是否为扇形”及“扇形弧长是否等于底面周长”。在小组讨论后，全班共同确定圆锥平面图的绘制步骤：

①确定扇形的半径（如4厘米）和圆心角（如90°），绘制扇形。

②计算扇形弧长（即底面周长）。

③根据周长计算底面半径，绘制底面圆形。

开普勒曾说：“我珍视类比胜于任何事物，它是我最信赖的老师，能揭示自然界的奥秘，在几何学中尤不可忽视。”通过演算数据绘制圆锥平面图，正是基于圆柱学习经验的类比推理。当平面图被制成实物圆锥时，猜测即被验证为真理。为进一步探究圆锥特性，教师可在制作过程中用细线穿过顶点与底面圆心，拉直后的两点间线段即为圆锥的高。通过对比高与扇形的半径，学生自然发现高短于扇形的半径，由此引出“扇形的半径称为圆锥的母线”这一概念。母线的引入顺理成章，高与母线的区别亦在学生认知中得以强化。

二、律动平面图形，描绘立体图纸——从“有形”到“无形”

学习往往遵循这样的法则：“观察事物时，需通过表象理解本质，体悟从无到有、由有归无的辩证过程，此为破解诸多问题的关键。”教学中，可通过旋转、叠加等操作将平面图形转化为“有形”的立体图形，引导学生观察并描绘其形态与生成过程，进而理解立体图形的本质规律，最终实现知识的“无形”内化与能力的隐性提升。

（一）快马扬鞭：洞悉本质，体验一个面的运动

1.旋转平面图，看见轨迹

通过快速旋转长方形、三角形硬纸板的操作活动，学生能够结合空间想象理解立体图形的形成过程。一是将长方形纸板贴于木棍，有两种贴法——以长或宽为轴旋转。观察不同旋转轴形成的圆柱差异，以及动画演示圆垂直平移形成圆柱的过程，揭示“同一立体图形可由不同平面图形通过不同运动方式生成”。二是直角三角形旋转实验。以直角边为轴旋转形成圆锥，对比以不同直角边为轴的结果差异；以斜边为轴旋转则生成双圆锥组合体。

【教学片段3】

师：圆柱由长方形旋转形成，圆锥可能由哪种图形旋转而成？

生1：三角形。

师：将直角三角形贴于木棒后快速旋转，观察结果。

生2：以直角边为轴旋转形成圆锥。

师：以不同长度的直角边为轴旋转，结果相同吗？

生3：不同。

师：以斜边为轴呢？

生4：形成双圆锥组合体。

师：普通三角形以任意边为轴旋转呢？

生5：类似直角三角形以斜边为轴旋转的结果。

通过对比圆柱与圆锥的生成过程，引导学生从运动视角理解立体图形的本质特征，强化学生观察、比较与想象能力。

2.手绘透视图，思维可视

小学教材中立体图形多以透视图呈现。教学中需说明透视图原理（圆转化为椭圆），指导学生绘制以长方形不同边为轴旋转形成的圆柱透视图，标注原图形位置并总结关联量关系（如半径与轴长的对应）。在动态绘制的过程中，学生会在脑内建构立体图形生成模型，并迁移至圆锥透视图的绘制：明确旋转轴对应高，另一直角边对应底面半径。透视图绘制将内隐思维显性化，通过图形转化关系揭示平面与立体的内在联系，促进学生空间观念与高阶思维的发展。

（二）豁然贯通：打破常规，想象多个面的叠加

1.叠加平面图，看见厚度

以圆片叠加为例，引导学生理解“体由面累积而成”的数学本质。

【教学片段4】

师：聪聪想做一个圆柱，就用卡纸剪出了很多圆片，他能做出一个圆柱吗？

生1：不能，做圆柱还需要一个长方形。

生2：可能可以，如果是很多圆片，将它们叠起来就得到圆柱。

师：这个想法很有创意。如果要叠起来形成圆柱，对这些圆片有什么要求？

生3：大小要一样。

师：想象一下，将100个、200个，甚至更多的圆片叠起来，形成什么？

生4：圆柱。

师：圆锥呢？可以由圆片叠加形成吗？

生5：我觉得每次叠加上去的圆片比上一张小一点点，慢慢叠加，直至小成一个点就形成圆锥了。

师：闭上眼睛试着想象。先放第一张圆片，再放比第一张小一点的第二张圆片，再放比第二张小一点的第三张圆片……放的圆片也越来越小，最后小到近似一个点。这便是圆锥。

通过实物操作与极限想象，学生直观感受圆柱与圆锥的叠加生成原理，感受极限思想与“化量为形”的数学方法。

2.建立对比表，知识构建

在辨析圆柱与圆锥特征后，教师可引导学生通过对比表（见表1）系统归纳异同，强化知识关联。

表格以直观、简洁的形式整合多维度信息，帮助学生系统性梳理知识脉络。表1通过对比圆柱与圆锥的特征差异，引导学生经历“观察→比较→抽象”的完整认知过程，使学生在归纳中反思、在辨析中内化，最终实现知识结构化后的“豁然贯通”。

“图”是贯穿圆柱与圆锥教学的思维之光。教师通过“绘制图→透视图→对比表”的阶梯式引导，将平面图形转化为立体模型，使抽象概念具象化；学生则通过“操作→绘图→想象”的实践路径，从“无形”的空间观念走向“有形”的几何建构，再升华至“体由面生”的数学本质理解。这一教与学的双向互动，正是深度课堂中知识生命力与学习内驱力的共同生长。

［ 参 考 文 献 ］

[1] 陈芳，邵汉民.单元整体设计    完善学习序列：以“三位数乘两位数”的单元教学为例[J].教学月刊小学版（数学），2019（3）：8-11.

[2] 束苏敏，林俊.在想象中丰富学习体验：《圆柱和圆锥的认识》教学设计与评析[J].小学教学设计（数学），2020（Z2）：111-113.

（责编    金    铃）