析·明·理：小学低段数学单元整体教学策略

［摘 要］单元目标的科学定位直接影响教学环节的有效实施与最终学习成效。针对小学低段学生普遍存在的“概念意义模糊混淆”“知识结构僵化”等问题，以教材的例题、习题为线索，通过“深耕细作，用活材料”“合纵连横，整合材料”等策略，精准锚定单元教学目标，帮助学生构建系统化知识体系，促进学生核心素养的发展。

［关键词］有余数除法；单元教学；单元整体教学

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）08-0066-03

《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）明确提出“要对内容进行结构化整合，探索发展学生核心素养的路径”。单元整体教学作为结构化整合的重要实施路径，要求教师立足单元视角，通过教材资源的系统整合，促进知识由分散走向系统化、学习由浅表迈向深度化。

数学教材单元作为独立的学习主题单元，其教学设计应聚焦学生数学核心素养的生长点。教师可以教材的例题、习题等为主线，通过整体分析单元内容确定教学目标，重构符合学生认知规律的教学序列。这种教学重构需要重点关注知识形成过程，强化数学思维训练，保持教学设计与学生个性发展的适配性，从而提升教学有效性。笔者在“有余数除法”单元教学中，通过精准诊断学习障碍、系统整合教学资源、创新实施单元教学，取得了显著成效。

一、析：寻障碍，明目标，让教学目标“有据可依”

“有余数的除法”作为人教版教材二年级下册第六单元的核心内容，在知识体系中具有承前启后的重要作用：既是对表内除法知识的拓展延伸，又为后续一位数除多位数的学习奠定认知基础。本单元以“理解余数含义”和“运用有余数除法解决实际问题”为核心目标，同步培养观察分析能力。但在教学实践中发现学生在学习该单元内容时存在两类认知障碍。

第一类：意义模糊混淆

学生在实际问题情境中难以建立被除数、除数、商、余数与具体量值的对应关系，导致解题时出现概念误用。例如在解决“22人划船，每船限乘4人，至少需几条船”问题时，学生会出现以下错误：

错例1：22÷4=5（条）……2（人） → 5+2=7条（数值误加）

错例2：22÷4=5（条）……2（人） → 5条（逻辑缺失）

此类错误的根源在于未能理解“商表征完整计量单位数量，余数反映剩余不可再分量”的本质，导致单位标注与解题策略选择失当。

第二类：知识结构断层

学生呈现碎片化知识存储状态，难以实现加减法与除法竖式的认知迁移。例如在“13根小棒搭正方形”探究活动中，学生会有以下做法：沿用加减法竖式结构直接记录运算过程；混淆包含除与等分除的竖式表达方式；机械模仿导致数位对齐错误。

这说明学生缺乏结构化认知图式，无法通过已有运算经验建构除法竖式模型。这些都直接影响学生后续迁移能力的发展。

基于上述分析，本研究立足单元整体教学视角，以人教版教材二年级下册“有余数的除法”为实践载体，系统构建单元结构化教学实施路径，为突破低段数学概念教学瓶颈提供可操作范式。

二、明：定目标，细要求，让教学规划“有章可循”

单元教学目标的确定是实施单元教学的首要任务，其导向作用如同航海指南针，为教学活动提供精准方向。通过系统分析学情，确立“有余数的除法”单元两大核心目标：其一，使学生在具体情境中理解有余数除法的数学本质，准确辨析商与余数的实际意义；其二，引导学生运用有余数除法解决实际问题，在提升分析能力过程中促进知识结构化建构。

在目标细化过程中，需注重学情与目标的适配性，确保目标设定兼具挑战性与可行性。例如将“体会有余数除法的含义”细化为“通过实物操作与直观观察，理解余数概念及有余数除法的算理，并能正确建立除法算式表征”。此类具体化目标能为教师提供明确的教学指引路径，同时强调目标的层次递进关系：在达成“理解余数及有余数除法含义”基础上，进阶设置“掌握余数必须小于除数的数学规律”目标。通过设计“搭一搭”“装蛋糕”等系列教学活动，构建螺旋上升的认知阶梯，帮助学生深度理解有余数除法的本质属性，系统培养学生的观察、分析与比较能力。

单元目标的确立与细化过程始终遵循“以生为本”原则，通过科学性原则保障知识逻辑严密，针对性原则聚焦学生认知痛点，可操作性原则确保教学实施路径清晰，为单元整体教学奠定坚实基础。

三、理：依目标，用材料，让材料应用“有标可对”

教学目标的导向性与教材素材的工具性构成教学设计的双重维度。教师应立足目标导向，通过教材资源的创造性使用，构建“目标—材料—发展”的良性互动机制，最终实现学生认知建构与能力发展的统一。

（一）深耕细作，用足材料

单元内各课时教学侧重点存在显著差异，对于“有余数的除法”，可实施“关键课例深度开发”策略，即对承载核心概念的课时进行精细化设计，在达成课时目标过程中同步推进单元整体认知建构。本单元核心目标体系包含三个层级：①理解余数概念及有余数除法的数学本质（概念层）；②掌握余数必须小于除数的数学规律（原理层）；③发展学生的观察、分析与比较能力（能力层）。教材通过两个典型例证展开：例1借助小棒摆三角形探究概念本质；例2通过摆正方形揭示余数性质和规律。笔者采用“一份材料，深度表征”，以“搭一搭”为核心内容，通过设计“摆三角形→拼正方形”的递进性探究活动，达成教学目标。

1.动作表征，直观操作感知意义

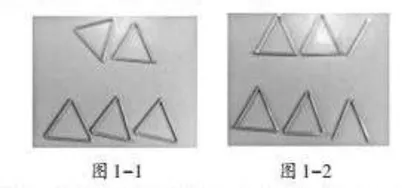
苏霍姆林斯基指出：“儿童的智慧在他的手指尖上。”教学中，教师应通过动手操作帮助学生建立直观认知。课始，笔者让学生用不同数量的小棒摆三角形，学生操作后呈现两类结果：用6根、9根小棒刚好摆成整数个三角形（如图1-1），用7根、8根小棒摆完后有剩余（如图1-2）。

学生在摆小棒时发现：6÷3=2（个）、9÷3=3（个）能整除，而7÷3=2（个）余1（根）、8÷3=2（个）余2（根）会出现剩余。通过对比，他们直观感受到余数的产生条件——当小棒数量不足3根时无法再摆一个三角形，因此余数只能是1根或2根。这种操作体验为理解“余数必须比除数小”奠定了实践基础。

“摆一摆”的实践活动使学生亲身体验了有余数除法的完整过程：从具体操作到算式表达，从发现问题到总结规律。这种方式既巩固了平均分的已有认知，又通过具象经验促进了抽象概念的建构，有效提升了学生的数学理解能力。

2.图式表征，数形结合理解意义

在摆小棒后，教师引导学生将操作结果转化为图式：<E：＼杂志社教学参考＼小教数学2025年第3期＼143.tif>可以用“③③”表示（无剩余），对应算式6÷3=2（个）。学生依此类推，<E：＼杂志社教学参考＼小教数学2025年第3期＼144.tif>可以用“③③①”表示，<E：＼杂志社教学参考＼小教数学2025年第3期＼145.tif>可以用“③③②”表示。通过看图说理，学生能清晰表述：“用7根小棒摆2个三角形剩1根，用8根小棒摆2个三角形剩2根。”这种图式表达帮助学生建立数形联系，为学生后续学习除法竖式打下基础。

在“装蛋糕”问题教学中，教师要求学生用图式表示22块蛋糕装盒过程：前5个盒子各装4块（○○○○），最后1个盒子装2块（○○）。通过对比图式，学生直观理解“装满5盒”与“至少需要6盒”的区别，明确商（5盒）和余数（2块）的实际意义，有效减少单位使用错误的情况。这种图式转化训练，使学生的具体操作经验逐步发展为抽象数学思维，提升了学生的空间想象与逻辑推理能力。

3.符号表征，数学模型内化意义

在摆小棒和画图示的基础上，教师引导学生将操作结果转化为数学符号。学生通过讨论明白：用7根小棒摆三角形写成7÷3=2（个）……1（根），用8根的写成8÷3=2（个）……2（根）。对比这些算式，学生发现余数总是比3小——摆三角形时，余数只能是1或2根。这种具体操作到符号表达的过程，帮助学生真正理解余数的数学规律。

教学全程仅用“摆小棒”一个核心活动，通过三个步骤层层推进：①动手摆出实际结果（动作理解）；②画出对应图示（图形表达）；③写出除法算式（符号抽象）。例如用9根小棒摆三角形时，学生先摆出3个三角形（动作），再画出“③③③”图示（图形），最后写出9÷3=3（个）的规范算式（符号）。

在后续“装蛋糕”问题教学中，教师延续这种方法：让学生先画5个装满4块蛋糕的盒子（○○○○），再画1个装2块的盒子（○○）。通过图示与算式22÷4=5（盒）……2（块）的对应，学生清楚看到“至少需要6个盒子”的解决方法。这种从具体到抽象的学习路径，使复杂问题变得直观易懂。

（二）合纵连横，整合材料

数学学科强调逻辑性和系统性，知识点间存在紧密联系。教学中，教师可精选教材例题与习题，按单元核心目标重组为连贯的学习任务。通过整合教材资源形成主题学习包，使碎片知识形成网络，促进学生思维深度发展。

1.“例、例”合纵——让知识在“纵向对比”中得到沟通

教材例题之间存在两种关联形式：一是前后例题形成认知阶梯，例如表内乘法（3×5=15）为本单元除法竖式奠定基础；二是不同形态的同类问题，如“分小棒”与“装蛋糕”问题本质相通。在教学中整合不同阶段例题，能有效串联知识脉络。笔者在教学例3除法竖式时，就把二年级上册表内乘法（一）例2、本册第六单元表内除法（一）例4整合起来（如图2）：

通过对比，学生发现，除法有“刚好分完”和“分不完有剩余”两种情况，为了体现分的过程，要清楚地在竖式中表示出分了多少，剩余多少，明确各数表示的意义。这种教学方法事半功倍，有助于学生更高效地掌握除法运算，为他们的数学学习打下坚实的基础。

2.“例、习”连横——让知识在“横向联系”中得到内化

教材习题具有巩固与拓展的双重功能。在“有余数除法”单元教学中，将例4与练习十四第4和第5题整合，可形成梯度训练（如图3）：

学生通过练习、比较，交流讨论发现：试商的过程就是利用口诀得到几与除数相乘最接近被除数，且小于它，就商几。

单元教学实践证明，教师通过“纵向贯通例题阶梯，横向整合习题资源”的系统设计，能使单元知识形成网状结构。这种教学方式不仅达成“掌握试商方法”的单元教学目标，更培养了学生类比迁移、归纳推理等核心素养。

总之，通过系统分析学情—精准定位目标—结构化重组资源，构建了“具身操作→图式转化→符号抽象”的认知发展路径，印证了单元整体教学对促进知识结构化、发展数学核心素养的实践价值，为小学数学深度教学提供了可复制的实施范式。

（责编    金    铃）